d라이브러리

Q

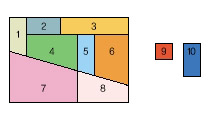
8개의 조각으로 옆 그림과 같은 직사각형을 만들었다. 여기에 정사각형 조각(9번)을 집어넣어 같은 크기의 직사각형을 만들 수 있을까? 그리고 다시 9번 조각보다 2배 큰 직사각형(10번)을 집어넣어 여전히 같은 크기의 직사각형을 만들 수 있을까?
 

A

지난 설 연휴에 일본 마술사 미스터 마릭의 쇼가 방영됐다. 다른 마술이야 눈에 잘 띄지 않는 눈속임을 이용하는 것이었지만 직사각형 모양의 블록에 작은 조각을 계속 덧붙여 가는 마술은 물리적인 트릭보다는 수학적인 원리를 이용한 것이어서 특히 흥미로웠다.

미스터 마릭은 문제의 그림에서 왼쪽과 같은 직사각형을 만든 다음 딱 맞게 구멍이 뚫린 틀을 끼워 보였다. 그 다음 9번 조각을 집어넣고 다시 그 틀을 끼워서 똑같은 직사각형임을 확인시키고, 10번 조각을 또 집어넣고 다시 한번 틀을 끼워 보여줬다.

물론 이 상황은 상식적으로도 수학적으로도 말이 안 된다. 조각을 덧붙였는데 똑같은 크기가 나올 수는 없는 일이니까. 물론 그 불가능한 일을 해 보이는 것이 바로 마술이지만.

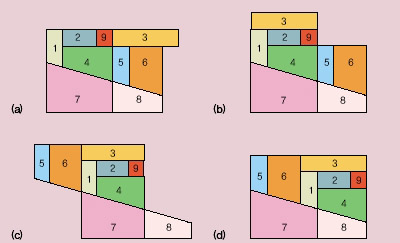
우선 9번 조각을 넣는 방법은 다음과 같다. 먼저 2번과 3번 사이에 9번을 끼워 넣는다(a). 미스터 마릭은 손으로 3번 조각의 튀어나온 부분을 슬쩍 가리고선 직사각형 모양을 만들었다며 익살을 부리기도 했는데, 다음 단계는 3번 조각을 위로 올리는 것이다(b). 그 다음 5번과 6번 조각을 왼쪽으로 옮겨 붙인다(c). 이제 마지막으로 할 일은 윗부분을 미끄러지듯이 움직여 7번과 8번에 맞추면 된다(d).

여기에 처음 보여줬던 틀을 끼우면 딱 맞으니 놀랍지 않은가? 실은 이것은 원래의 직사각형과는 달리 세로가 아주 조금 길지만, 처음에 미스터 마릭이 보여줬던 틀의 구멍이 약간 여유 있게 만들어져 있었으니 언뜻 봐서는 딱 맞는 것처럼 보일 수밖에 없다.

자, 이제 여기에 10번을 집어넣을 차례인데, 그 놀라운 방법을 쓰기에는 지면이 부족하다. 독자 여러분들이 직접 이 페이지를 잘라서 해 보시라. 나중에 과학동아 한 권을 새로 사는 것 잊지 마시고.
 

지난달 정답_23