d라이브러리

Q
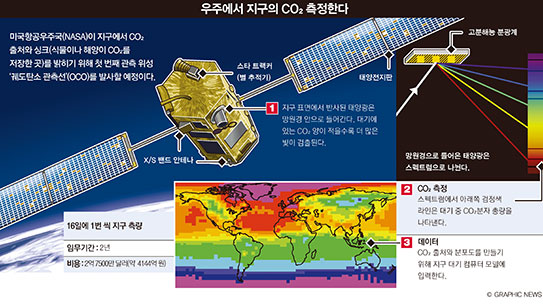
참말만 하는 기사와 거짓말만 하는 건달이 사는 섬에 여행 갔다가, 만찬에 초대받았다. 참석자들은 50쌍의 부부였는데, 각 부부는 기사와 기사, 건달과 건달, 또는 기사와 건달일 수도 있다. 가이드가 질문을 하나 알려 주면서, 이 질문을 하면 각 부부가 어떤 사람인지를 알 수 있다고 했다. 물론 이 가이드는 기사다. 그런데 그 질문을 했을 때 어느 한쪽의 대답만으로는 응답자는 물론 그 배우자가 어떤 사람인지 전혀 알 수가 없었다. 대신 양쪽의 대답을 조합하면 그들이 어떤 사람인지를 알 수 있었다. 그 질문을 50명의 남편들에게 했더니, 그들은 모두 “예”라고 대답했고, 같은 질문을 50명의 부인들에게 했더니, 그들은 모두 “아니오”라고 대답했다. 그렇다면 거짓말을 한 사람은 몇명일까?

A
쉽게 50명이라고 대답하는 사람이 많을 것이다. 총 1백명이 같은 질문에 반은 “예”, 반은 “아니오”라고 했기 때문이다. 쉬운 문제를 냈냐고 따지고 싶겠지만 이는 정답이 아니다.

부부는 (부인, 남편)에 대해 (기사, 기사) (기사, 건달) (건달, 기사) (건달, 건달) 4가지 경우가 가능하다. 그리고 부부 둘의 대답으로 가능한 가짓수도 (예, 예) (예, 아니오) (아니오, 예) (아니오, 아니오) 4가지다.

문제에서는 부부의 대답으로 이 4경우를 구분할 수 있다고 했다. 따라서 부부의 대답 4가지와 4부류의 관계가 1:1이어야 한다. 또 문제에는 한사람의 대답만으로 본인은 물론 배우자의 정체를 알 수 없다고 했다. 따라서 2조건에 부합하는 대답이 뭔지를 알아보기 위해 다음과 같은 표를 만들어보자. 그리고 (예, 예)를 임의로 (기사부인, 기사남편) 커플에 놓아보자.

2번째 조건에 만족하려면 (예, 예)와 같은 세로줄에 있는 답변에는 (예, 아니오)가 나올 수 없다. 만약 그렇다면 부인의 대답만으로 남편이 어떤 사람인지를 알 수 있기 때문이다. 같은 식으로 같은 가로줄에 있는 답변에서도 (예, 아니오)가 나올 수 없다. 만약에 (예, 아니오)가 나온다면, 부인의 대답만으로 자신이 어떤 사람인지를 알 수 있기 때문이다. 따라서 (예, 예) 칸과 세로 또는 가로로 같은 칸에는 (아니오, 예)나 (아니오, 아니오)가 들어가야 한다. 그러면 남은 한칸의 가능한 대답은 (예, 아니오)가 된다(표).
 

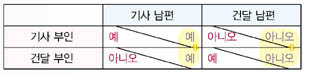
하지만 이 결과는 부인에 대해서는 2조건을 만족시켰지만 남편은 그렇지 못하다. 남편의 답변만으로 남편이 어떤 사람인지를 알 수 있다. 남편의 대답이 예면 기사고 아니오면 건달이라고 드러나기 때문이다. 애초에 이런 질문은 존재할 수 없는 것이다.

그러므로 거짓말한 것은 1명, 바로 출제자인 필자다. 필자가 항상 거짓말만 하는 건달이냐고? 다시 한번 문제를 읽어보시라. 필자는 거짓말한 사람이 몇명이냐고 물었지, 건달이 몇 명이냐고 묻지 않았다.