d라이브러리

대칭성은 고대부터 미(美)의 대명사였다. 이와 마찬가지로 과학에서도 대칭은 중요한 요소로 여겨왔다. 하지만 최근 대칭성이 흔들리고 있다. 특히 빅뱅 이후 물질과 반물질 중 물질만이 남아있는 문제에서 더욱 대칭성이 깨지고 있다. 반물질 연구에 왜 대칭성이 중요한 것일까.

대칭은 완벽함의 대명사다. 다보탑이나 석가탑이 신라시대 대표적인 조형물로 인정받는 것도 마찬가지 이유에서다. 좌우의 대칭성이 절묘해 미적인 아름다움이 최고 수준에 달한 것으로 평가받는다. 사실 고대에서 현대에 이르기까지 대부분의 건축물은 대칭적으로 지어졌다.

왜 사람은 대칭을 추구할까. 아마도 완벽함으로부터 오는 미(美)와 대칭에서 오는 설계의 용이성 때문이지 않았을까.

자연의 신비로움도 대칭에 이르면 경탄할 만하다. 거의 모든 생물체는 한개 이상의 대칭을 가진다. 가장 일반적인 경우가 좌우 대칭이다. 꽃들은 꽃잎의 수에 따라 다양한 대칭을 가지고 있다.

그러나 자세히 보면 대칭이 정말로 완벽하지만은 않다는 사실을 알 수 있다. 예를 들어 사람의 얼굴은 좌우가 거의 대칭인데, 머리의 가르마는 한쪽으로 돼 있다. 이처럼 대칭성이 깨지는데서 또다른 조화가 이뤄지고 있는 것을 볼 수 있다. 현대의 예술가는 일부러 대칭성을 깨려고 시도한다.

물리학자에게 대칭은 어떤 의미가 있을까. 우선 자연을 이해하는데 대칭성은 매우 중요한 역할을 한다. 물리학자에게 대칭성은 자연이 준 가장 큰 선물과도 같다. 대칭성을 도입하면 어려운 문제가 쉽게 이해되는 경우가 종종 있으며, 대칭성을 물리법칙의 기본으로 인식할 수 있다.

좌우를 구분하는 자연

물리적으로 대칭이란, 어떤 계에 특정한 변환을 가했을 때, 물리법칙이 변하지 않고 똑같이 적용될 경우 이 변환에 대해서 대칭이라고 한다. 어떤 변환에 대해 대칭이면 그 대칭성에 해당되는 보존법칙이 존재한다.

예로는 좌표의 원점을 수평이동하는 경우다. 좌표의 원점을 서울에서 부산으로 바꿔도 뉴턴의 힘의 방정식은 그대로 적용된다. 이런 대칭에 해당되는 법칙이 바로‘운동량의 보존법칙’이다. 갈릴레이가 살던 시대에나, 아리스토텔레스가 살던 시대에나 물리법칙은 똑같이 적용된다는 점에서 에너지 보존법칙을 찾아낼 수 있다.

이같은 좌표 원점의 수평이동과 같은 변환은 공간을 미소하게 변환시키는 일을 반복함으로써 연속적으로 이뤄질 수 있기 때문에 연속변환이라고 한다.

한편 거울을 보고 물리현상을 기술하면 어떻게 될까. 이 경우는 좌우를 반전시키는 과정으로 공간을 아무리 연속적으로 변환한다 하더라고 좌우를 바꿀 수는 없다. 이와 같이 연속적으로 변환이 안되는 변환을 불연속변환이라고 한다.

공을 오른손에 들고 거울 앞으로 다가가자. 그리고는 오른손에 있던 공을 왼손으로 던져보자. 거울에는 왼손에서 오른손으로 공이 던져진 상황이다. 이 경우에 물리법칙이 바뀌었을까. 아니다. 좌우만 바뀌었을 뿐 뉴턴의 운동방정식은 똑같이 적용된다. 이같은 공간반전을 물리학에서는‘패리티(P, Parity)변환’이라고 한다. 공간반전(P변환)을 해도 물리현상이 변하지 않았다면(즉 좌우를 구분하지 않는다면) P에 대해 물리현상은 대칭이고 이 경우에 보존되는 물리량은 패리티다.

물리학의 오랜 역사 속에서 P대칭성은 불변의진리라고여겼다. 그러나1950년대들어 P대칭성이 깨질 수 있다(또는 보존되지 않는다)는 이론이 제기됐다. 당시 입자물리학의 큰 수수께끼 중 하나였던 하나의 입자가 패리티가 양인 경우와 음인 경우로 모두 붕괴하는 문제를 풀다가, 1956년 두 젊은 중국인 이론물리학자 리와 양은 약한 상호작용에서 P대칭성이 깨질 수 있다는 논문을 발표했다. 이는 커다란 발상의 전환이었다.

곧바로 실험물리학자인 우여사가 코발트 원자핵의 베타붕괴에서 P대칭성이 깨지는 것을 실험으로 확인했으며, 곧이어 π입자를 포함한 다른 소립자의 붕괴에서도 확인되면서 리와 양의 이론은 확고하게 굳어지게 됐다. 물리학자가 오랫동안 신봉했던 대칭성이 깨진 것이다.‘ 자연이 좌우를 구별한다.’이는 물리학자들에게는 매우 이상한 현상이었다. P대칭성이 깨진다는 사실은 곧바로 물리학에서 중요하게받아들여졌다. 1957년 리와 양은 노벨 물리학상을 수상했다.

소립자 세계의 왼손잡이와 오른손잡이
 

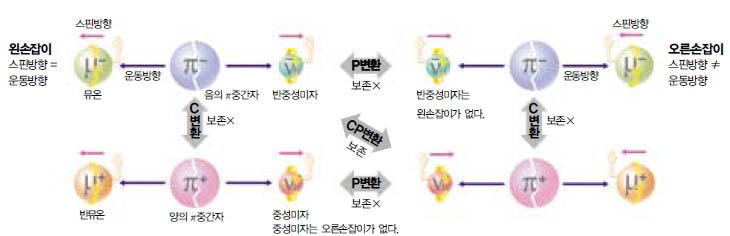
물리학자에게 P대칭성 깨짐이 왜 이토록 중요한 문제일까. 이는 입자의 전하를 반대 부호로 치환하는 즉, 입자를 반입자로 치환하는C(Charge)변환이 깨진다고 해석될 수있기 때문이다.

이를 알아보기 위해 우선 소립자 세계에서 왼손잡이와 오른손잡이를 정하는 방법을생각해보자. 입자들은 질량, 전하와 같은 성질 외에도 스핀이라는 고유 성질을 가진다.스핀은 팽이의 회전쯤으로 생각하면 된다.

팽이를 돌려서 위에서 보았을 때 시계반대방향으로 회전하면 스핀의 방향은 위로 정하자. 반대로 시계방향으로 회전하면 스핀 방향을 아래로 정하자. 물리학자는 입자의 운동방향에 대한 스핀방향에 따라 왼손잡이인지 오른손잡이인지를 정하는 방법을 택한다. 즉 운동방향과 스핀방향이 같으면 오른손잡이, 반대면 왼손잡이로 본다는 말이다.

이제는 P대칭성과 C대칭성 문제로 되돌아가자. 우선 거울을 다시 한번 보자. 진행방향에 대해 오른쪽으로 회전하고 있는 공을 거울을 향해 던져보자. 거울 속의 공은 내 쪽으로 가까이 다가오는데 진행방향에 대해 왼쪽으로 회전하는 것을 알 수 있다. 이같이 P변환은 왼손잡이를 오른손잡이로, 또는 그 반대로 변환시킨다.

실제로 소립자 중 하나인 π중간자라는 입자의 붕괴를 P변환시켜보자. 이 입자는 일본의 유가와가 그 존재를 예측해 노벨상을 받게 해준 입자이다.

(-)전하를 띤 π중간자는 뮤온과 반중성미자(중성미자의 반입자)라는 입자로 붕괴한다.

즉π(수식)로 붕괴한다. 이때 입자들의 스핀에 유의해야 한다. π중간자는 스핀이 0인 반면에 뮤온과 반중성미자는 스핀이 각각 1/2이다. 스핀도 붕괴과정에서 보존돼야 하기 때문에 두 입자의 스핀의 합은 0이 돼야 한다. 따라서 두 입자의 스핀의 크기는 같지만 방향은 반대가 돼야 한다는 말이다.

만약 π중간자가 정지해 있다가 붕괴한다면 뮤온과 반중성미자는 운동량보존의 법칙에 따라서 서로 반대방향으로 날아가야 한다. 그렇다면 뮤온과 반중성미자는 각각 어떤 손잡이가 될까. 서로 같은 손잡이여야 한다. 왜냐하면 뮤온과 반중성미자의 스핀방향도 서로 반대여야 하기 때문이다. 따라서 뮤온이 왼손잡이이면 반중성미자도 왼손잡이여야 하고, 뮤온이 오른손잡이면 반중성미자도 오른손잡이여야 한다.

그런데 여기서 문제가 발생한다. 뮤온은 왼손잡이도 있고 오른손잡이도 있는데, 반중성미자는 오른손잡이 밖에 없다. 최소한도 필자가 아는 한에는 왼손잡이 반중성미자를 보았다는 사람은 아직 없다. 따라서 뮤온도 반중성미자도 모두 오른손잡이여야 한다.

그렇다면 π중간자의 붕괴현상은 P대칭성이 보존될까. 오른손잡이를 왼손잡이로 바꾸는 P변환을 시켜보자. P변환을 시키면 두 붕괴 입자 모두 왼손잡이여야 하는데 반중성미자는 왼손잡이가 없지 않은가. 즉 거울 속의 세계에서는 음의 π중간자가 같은 방식으로 붕괴할 수 없고 P대칭성이 100% 깨져있는 것이다.

그렇다면 π중간자 붕괴에서 C대칭성은 보존될까. C변환은 입자의 전하를 바꿔주는것이다. 따라서 음의 π중간자 붕괴현상의 C변환은 (수식)이다(음의 π중간자는 양의π중간자로, 뮤온은 반뮤온으로 반중성미자는 중성미자로 바뀐다).

하지만 C변환은 손잡이를 바꾸지는 않는다. 그러니까 이번에는 오른손잡이 반뮤온과오른손잡이 중성미자로 붕괴하는 것이다. 하지만 반중성미자는 오른손잡이 밖에 없다는것처럼 중성미자는 왼손잡이 밖에는 없다. 결국 C변환을 해보면 이런 붕괴는 일어날 수 없다. C대칭성도 P대칭성과 마찬가지로 100% 깨져 있다는 것이다.

뇌종양 검진에 이용되는 반입자

이같은 대칭성 문제를 물리학자는 쉽게 포기하지 않았다. 약간만 생각해보면, C와 P변환을 동시에 하면 문제가 없다는 것을 알 수있다. 음의 π중간자 붕괴현상을 C변환에다가 다시 P변환을 시키면 양의 π중간자가 왼손잡이 반뮤온과 왼손잡이 중성미자로 변해 이 붕괴는 아무런 문제없이 일어날 수 있다. CP변환을 시키면 대칭성이 복원되는 것이다. 물리학자는 공간을 반전시키는 동시에 전하를 반전시키면 대칭성이 유지되는 것으로 대칭성 문제에서 한발자국 물러섰지만, CP대칭성이야말로 깨지지 않는 대칭성이라고 생각하게 됐다.

그러나 이러한 믿음도 잠시, 1964년 피치(V.Fitch)와 크로닌(J.Cronin) 등에 의해 K중간자의 붕괴에서 CP대칭성이 깨지는 실험 결과가 나오면서 그마저 포기하기에 이르렀다. 피치와 크로닌은 많은 물리학자들에게 자연에 대한 배신감을 준 공로로 1980년에 노벨상을 수상했다.

CP대칭성은 π중간자 붕괴에서 본 것처럼 소립자 세계에서 입자와 반입자의 대칭성과밀접한 관련을 맺고 있다. 입자를 반입자로 바꾸려면, 단순히 전하만 바꾸면 되는 것이 아니고 공간반전을 동시에 시켜주어 왼손잡이와 오른손잡이도 바꿔주어야 하는 것이다. CP대칭성은 입자와 반입자(또는 물질과 반물질) 사이의 대칭성이다.

반물질은무엇인가? 물질을 이루는 기본단위가 입자이듯이 반물질을 이루고 있는 기본단위가 반입자이다. 소립자의 세계에서 반입자는 일상적으로 존재하는 것으로 전혀 새로운 것이 아니다. 반입자는 입자와 질량과 평균수명 등은 같지만 전하와 내부양자수(예를들어 경입자수와 같은 것)가 반대인 입자다. 전자의 반입자는 양전자이고 양성자의 반입자는 반양성자이다. 보통 사람들이 잘 아는 수소원자는 양성자에다 전자를 하나 결합시킨 것이다. 반입자인 반양성자에다 양전자(전자의 반입자는 특별히 양전자라고 부른다)를 결합시키면 반수소원자가 될 것이고 이들을 많이 모아 놓으면 태양과 같은 별이 되지 말라는 법도 없다.

실제로 반수소원자를 만드는 연구가 진행중이고 매우 짧은 순간밖에 살지 못했지만 반수소원자를 만들었다는 보도도 있었다(과학동아 2000년 9월호 참조). 반입자인 양전자는 이미 양전자단층촬영(PET)이라는 장치에 사용되고 있으며 우리나라도 일부 병원에서 이미 뇌종양 등의 검진에 사용하고 있다.

그렇다면 반입자는 어떻게 만들어지는것일까. 입자가속기는 양전자의 빔으로 전자의 빔과 충돌시켜 전자-양전자 소멸을 통해 새로운 입자를 만든다. 물론 새로운 입자는 항상 입자-반입자의 쌍으로 생성된다. 이렇게 입자와 반입자는 항상 쌍으로 생성되는데 왜 우리 주변에는 반물질이 없을까.

'반 사람과 악수를 한다면?

우선 있다면 큰일날 일이다. 내 옆에 반물질로 된 사람이 있다고 해보자. 나와 이 사람은 완전한 진공 중에 있다고 가정해야 한다.

‘반’사람은 어떻게 보일까. 보통 사람과 전혀 구분할 수가 없다. 우리가 무엇을 볼 때는 빛을 통해서 보는데 빛은 물질과 반물질을 구분할 줄 모른다. 그렇다면 반물질로 돼 있는지 어떻게 알 수 있을까. 두사람이 악수를 하는 순간 엄청난 폭발을 하면서 두사람의 손은 없어지고말것이다. 반물질이 우리 주변에 없다는게 얼마나 다행스러운일인지 모른다. 항상 처음 보는 사람과 악수를 할 때‘반’사람인지 물어보는 번거로움이 없으니 말이다.

그런데 문제는 빅뱅에 의한 우주의 생성 이후에 물질과 반물질이 같은 양으로 생겨났을터인데 어찌해서 모두 소멸해서 빈 공간이 되지 않고 현재의 우주처럼 물질로만 이뤄져 있는 우주로 진화했느냐는 것이다. 아직까지 이를 쉽게 설명할 수는 없지만 많은 물리학자들이 이 문제를 놓고 열심히 연구하고 있다.

하지만 물질로만 이뤄진 현재의 우주가 있기 위한 중요한 조건 중의 하나는 물질과 반물질의 대칭성인 CP대칭성이 깨져 있어야 한다는 것이다. 그런 면에서 CP대칭성 깨짐의 발견은매우고마운일이아닐수없다. 만약 CP대칭성이 완벽하다면, CP대칭성이 깨졌다는 사실을 알았을 때보다 훨씬 더 많은 고민을 해야 했을지도 모른다.

1964년에K중간자에서 CP대칭성 깨져 있다는 것이 발견되고 난 후 물리학자들은 이런 기괴한(?) 현상에 대해서 여러가지 이론을 제시했다.

973년 일본의 이론물리학자인 고바야시 마스카와는 자연에는 최소한 3세대 6개의 쿼크가 있어야 하고 이들 사이에 섞임 현상이 존재하면 K중간자에서 CP대칭성이 깨지는 것을 설명할 수 있다는 이론을 발표했다. 최소한 6개의 쿼크가 있어야 섞임행렬 요소에 복소수 위상이 나타날 수 있고 이복소수 위상이 CP대칭성 깨짐을 준다는 것이다. 만약에 2세대 4개의 쿼크만 존재한다면 섞임행렬의 요소들이 모두 실수로만 구성되며 CP대칭성이 깨지는 방법은 표준모형 내에서 찾아내기가 매우 힘들다.

미국 대일본의 가속기 경쟁
 

이 이론이 발표되던 당시에는 3개의 쿼크만이 알려져 있었기 때문에 매우 획기적인 이론이 아닐 수 없었다. 하지만 1974년 참쿼크의 발견을 필두로 1995년 톱쿼크의 발견까지 6개의 쿼크가 모두 발견됐다.

고바야시와 마스카와의 이론이 맞다면 다른 입자에서도 CP대칭성이 깨지는 현상이 나타나야 하는데, 1964년 이후 40년간 K중간자 외에서는 CP대칭성이 발견되지 않았다.

B중간자라는 입자에서 CP대칭성을 측정하기 위한 실험들이 1980-90년 초에 제안됐고 1994년경부터 이를 위한 입자가속기 건설이 시작됐다. 이 실험을 위해 수천만개의 B중간자 쌍이 필요하므로 이를 만들어내는 가속기를 B-공장이라고 부른다. B중간자에서 CP대칭성 깨짐의 발견은 현재의 이론이 이 현상을 제대로 설명할 수 있느냐는 점은물론 새로운 이론이 발붙일 자리를 찾는면에서 매우 중요하다.

이 중요성에 비춰 미국의 스탠포드 가속기 연구소(SLAC)와 일본의 고에너지 가속기 연구소(KEK)에서 거의 동시에 가속기를 건설했다. 이들 두 가속기에는 벨(BELLE, KEK)과 바바(Babar, SLAC) 두 실험그룹이 결성됐으며, 서울대, 고려대, 연세대, 성균관대,경상대, 경북대의 6개 대학 약 20여명의 한국의 연구자들이 대거 벨 실험에 참여했다.

두그룹은 1999년부터 실험을 시작했고 지난 7월에 각각 B중간자의 붕괴에서 CP대칭성 깨짐 현상을 발견했다고 발표했다. 정확히 말하면 B중간자와 반B중간자가 특정한 붕괴모드로 붕괴하는 시간 분포가 비대칭이라는 것을 측정했다고 발표했다. 이로서 40년전 K중간자에서 CP대칭성 깨짐이 발견된 후 처음으로 다른 입자에서 CP대칭성이 깨지는 현상을 발견한 것이다.

이로써 표준모형 안에서 고바야시 마스카와 이론이 정말로 CP대칭성 깨짐의 원인을제공하는지에 대한 정밀 검증이 가능해졌다고할수있다. 이번의결과는오차범위내에서 표준 모형의 예측과 틀리지 않다.

향후 정밀측정에 의해 이 이론이 예측하는 CP대칭성과 차이가 난다면 새로운 이론이 도입될 가능성이 있다. 한편 많은 이론물리학자들이 현재 표준모형이 예측하는 CP대칭성 깨짐보다도 더 강한 깨짐이 있어야 현재 우주의 물질 존재를 기대할 수 있다고믿는다.

또다른 의문은 P나 CP대칭성이 약한 상호작용에서만 깨져 있고 다른 상호작용인 전자기력이나 강한 상호작용에서는 아직까지 그 대칭성 깨짐이 관측된 바가 없다. 언제나약한 놈이 깨지기 마련일까. 전자기력이나 강한 상호작용에서 CP대칭성은 과연 문제가 없는지도 향후의 연구대상 중 하나로 볼 수 있다. 그러므로 CP대칭성의 깨짐에 대한 연구는 이제 막 시작한 단계나 마찬가지이다.

CP대칭성 깨짐의 측정법

B중간자에서 CP대칭성이 깨지는 것을 어떻게 측정하는지 알아보자. 이를 위해 우선 B중간자의 진동현상을 이해해야 한다.

중성 B중간자는 b(바톰)쿼크와 반d(다운)쿼크로 만들어진 입자이다. 따라서 반B중간자는 반b쿼크와 d쿼크로 만들어져 있다. 물론 그래야 서로 반입자가 된다. 그런데 쿼크사이의 섞임에 의해 b쿼크가 d쿼크로 반d쿼크가 반b쿼크로 동시에 변하는 일이 가능하다. 즉 B중간자가 반B중간자가 되는 것이다. 이 현상은 일정한 시간 주기를 두고 반복되며 그래서 이를 진동현상이라 부른다.

이 진동현상은 이미 실험적으로 잘 알려져 있는 것이다. 중성 B중간자의 붕괴를 보면 CP 모드라는 특정한 붕괴가 있다. 이 경우에 붕괴가 B중간자로부터인지 아니면 반B중간자로부터인지 알 수가 없다. 그러므로 이 붕괴는 처음의 B중간자로부터 붕괴했을 수도 있고 한번 진동한 후 반B중간자로부터 일 수도 있다.

이렇게 두가지 가능성이 있기 때문에 이 경로 사이에 간섭현상이 일어난다. 이 간섭에 의한 효과가 바로 쿼크간 섞임행렬에 있는 복소수 위상때문에 나타난다. 그런데 처음에 B중간자로 시작한 경우하고 처음에 반B중간자로 시작한 경우에 이 특정 붕괴로 가는 시간 분포를 보면 이런 간섭현상에 의해 서로 비대칭적이라는 결과가 나온다. 이를 CP비대칭도라고 한다.

문제는 평균 수명이 수조분의 1초 정도밖에 안되므로 이 짧은 시간 안에 각각의 붕괴의 시간변화를 측정해 미소한 차이를 찾아내는 것이다.

KEK와 SLAC의 가속기들은 전자와 양전자의 에너지를 다르게 해 생성된 입자들을 한쪽으로 추진(부스트)시켜 좀더 멀리 날아가도록 해 이런 측정이 가능하도록 만들었다. 한편 이들 가속기에서 B중간자와 반B중간자가 쌍으로 생기기 때문에 한쪽이 B나 반B인지 알 수 있는 다른 붕괴모드로 붕괴한 경우를 측정하면 된다. 한쪽이 B로 확인된다면 다른 쪽은 바로 그 시간에 반B이기 때문이다.

결국 이 두가지 붕괴 사이에 시간분포가 한쪽이 B인 경우와 반B인 경우를 나눠서 측정한 후 그 분포가 비대칭인지를 확인하면 된다. 벨 실험에서 측정한 시간 분포를 살펴보면 두 경우에 분포가 비대칭이라는 것을 한눈에 알 수 있다.