d라이브러리

피아노의 '도'음과 바이올린의 '도'음은 같지만 다르다.진동수가 동일하다는 점은 같지만 음색이 차이나기 때문이다.사실 피아노의 '도'음은 여러가지 파동이 합쳐진 것이다.이것은 바이올린의 경우도 마찬가지다.어떤 파들이 합쳐지는가에 따라 같은 음이라도 음색이 다르게 나타난다.

일상생활 속에서는 수없이 많은 소리를 접할 수 있다. 여기에는 한여름의 매미 소리, 때때로 지나가는 비행기나 자동차 소리, 그리고 천둥소리 같은 자연음과 사람들이 즐겨듣는 음악이 있다. 클래식, 유행가, 팝송, 랩, 재즈 등 인간의 희노애락을 다양한 음으로 표현하는 음악. 과학과는 멀리 떨어져 있을 것 같은 이 음악도 알고 보면 과학과 닿아있다.

따뜻한 곳에서 연주하면 음정이 변한다

음정(높은 음과 낮은 음)의 차이나 한 옥타브의 차이는 어디서 비롯되는 것일까.기타 줄이 얇을수록 높은 음이 만들어지는 이유는 무엇일까.기타의 세번쨰 줄에서 다양한 음을 만들 수 있는 까닭은 무엇일까.또 같은 도(C)음이라도 피아노와 바이올린,또는 사람의 음색은 명확히 구분되는데 그 원인은 무엇일까.이같은 궁금증들을 음악 속에 숨어있는 파동의 조화로 풀어보자.

기타를 조금이라도 연주해본 사람이라면, 기타줄의 굵기가 가늘수록, 같은 줄이라도 줄을 팽팽하게 할수록 높은 음이 난다는 점을 잘 알 것이다. 또 똑같은 줄이라도 공명통에 가까운 곳을 짚느냐, 먼 곳을 짚느냐에 따라 음정의 높낮이가 달라진다. 기본음(E, A, D, G, B, E)을 내는 여섯 개의 줄에서 다양한 음정을 얻을 수 있다는 얘기다.

현의 길이가 바뀌면 현에 생기는 정상파의 파장이 변하면서 음의 높낮이가 달라진다. 현의 길이가 짧아질수록(즉 왼손가락이 공명통에 가까워질수록) 음정은 높아진다. 음의 높이가 파장에 대략 반비례하기 때문이다.

현에서 파동의 전파 속도를 v, 파동의 진동수와 파장을 각각 ν, 및 λ라고 하면 파동의 속도는 진동수와 파장의 곱으로 나타난다(v= ν×λ). 그리고 현의 장력과 선밀도(단위 길이당 질량)을 각각 T와 μ라고 할 때 파동의 속도는 현의 장력을 선밀도로 나눈 값의 제곱근으로 표현된다(v=
$\sqrt{T/μ}$).

이 두가지 식으로부터 장력과 선밀도가 고정돼 있는 현의 경우 파의 전파속도가 일정하므로 파장이 길어질수록 진동수가 줄어들어서 낮은 음이 만들어진다는 것을 쉽게 알 수 있다. 반면 현의 길이가 같으면(즉 파장 λ가 같은 경우) 현이 굵을수록 선밀도가 커지고 현에서의 파의 전파속도가 작아지므로 음의 진동수도 작아져서 낮은 음이 난다. 장력을 증가시켜서 현을 팽팽하게 해주면 반대로 파의 전파속도가 커지므로 현의 길이가 고정되어 있으면 더 큰 진동수를 얻는다. 고음을 얻을 수 있다는 말이다.

그리고 똑같은 악기라도 평소보다 온도가 높은 곳에서 연주하면 음정이 달라진다. 바이올린과 같은 현악기를 따뜻한 곳에서 연주하면 현이 늘어나기 때문에 장력이 줄어들어 전파속도가 줄어 음정이 약간 내려간다. 반면 따뜻한 곳에서 음파의 속도는 증가하므로 관악기의 음정은 현악기와는 반대로 높아지는 경향을 보인다. 관악기는 현악기와 달리 파장의 길이는 고정적이다. 따라서 손으로 구멍을 막으면서 음관의 길이를 변화시키더라도 진동하는 공기기둥의 길이는 변하지 않는다. 때문에 음파의 속도가 증가하면 진동수가 커진다.

한 옥타브 위의 음은 기본진동수의 2배

기타줄을 퉁긴 후 현의 진동을 자세히 들여다보면,여러 형태의 서로 다른 파형이 중첩 돼 있음을 발견할 수 있다.이것은 음색에 영향을 미치는 배음과 관련이 있다.양끝이 고정돼 있는 현을 튕길 때에 발생하는 정상파의 파장은 반파장의 정수배가 된다.그리고 반파장의 정수배는 현의 길이가 된다(그림1).
 

파장이 현의 길이의 2배가 될 때의 진동수를 현의 기본진동수라고 한다. 그 외의 진동수는 기본진동수의 정수배가 되는데 이들을 배음이라고 부른다. 배음들의 진동수는 기본진동수보다 크므로 높은 음정의 소리들이 나온다. 그렇다면 진동수와 음정과의 관계는 어떻게 될까.

서양음악에서는 1옥타브 사이에 12음이 들어있다. 이것을 평균율이라고 한다. 평균율에서는 1옥타브를 반음씩 12등분했기 때문에 반음에 해당하는 진동수비가 같다. 따라서 각 반음에 대응하는 진동수의 비는 ${}^{12}$$\sqrt{2}$=1.059로 정해야 한다. 이때 각 반음의 진동수는 일정한 비율인 ${}^{12}$$\sqrt{2}$배로 증가해서 1옥타브 올라가면 원래 음 진동수의 2배가 되는 등비수열을 이룬다. 진동수가 기본진동수의 2배가 되면 1옥타브 위의 소리를 얻고, 4배가 되면 2옥타브 위의 음이 된다는 말이다.(그림2).

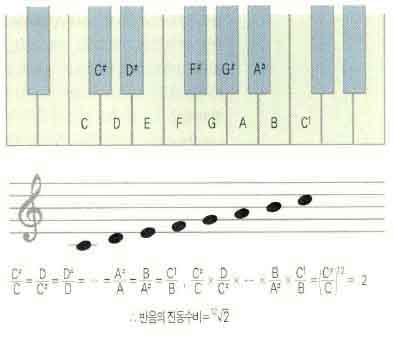
우리가 잘 아는 가온 다(C)음(피아노의 ‘다’음 중에서 가운데에 가장 가까이 위치하고 있는 건반에 해당하는 음)의 진동수는 2백64Hz로 정의돼 있다. 모든 다(C)음은 이 진동수의 ${2}^{n}$진동수를 가지는 음들로 이루어져 있다. 여기서 n은 음수와 영을 포함한 정수들이다. 만일 n=1인 진동수 5백28 Hz의 음은 가온 다음(2백64 Hz)보다 한옥타브 높은 다(C)음이 되며 이 음을 통상 C1으로 나타낸다. 반대로 n=-1인 진동수 1백32Hz의 음은 가온 다음보다 한 옥타브 아래의 다음이 되며 C1으로 나타낸다. 그리고 가온 다음과 같은 옥타브 상의 D, E, F, G, A, B음의 진동수는 2백97Hz, 3백30Hz, 3백52Hz, 3백96Hz, 4백40Hz, 4백95Hz로 정해져 있다. 이러한 표준은 1939년에 맺어진 런던 국제 협약에 근거한 것이다. 전자식 신시사이저(synthesizer)로는 음정과 진동수가 여기에서 설명한 것처럼 연관되어 있다는 사실을 손쉽게 확인해 볼 수 있다.

현에서 만들어지는 다양한 음정

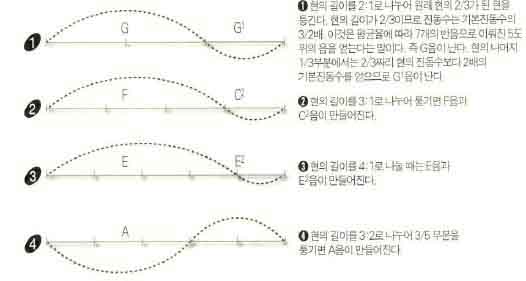
기본진동수가 가온 다음인 현에서 기본진동수의 3배가 되는 진동수를 가지는 음정은 무엇일까. 이를 위해 원래 현의 길이를 1:2로 나누어 길이가 원래 현의 2/3 가 된 현을 퉁겨보면 그 소리는 G음이 된다. 현의 길이가 2/3으로 된다는 것은 진동수는 기본진동수의 3/2배(=${}^{12}$$\sqrt{{2}^{7}}$). 평균율에 따라 7개의 반음으로 이뤄진 5도 위의 음을 얻는다는 말이다. 만일 나머지 1/3 부분을 퉁겨보면 이때는 2/3짜리 현보다 2배의 기본진동수를 얻게 되므로 G 음에 비해 1옥타브 위의 음인 G¹음(가온 다음의 12도 위 음)을 얻는다.

마찬가지로 가온 다음인 현을 1:3으로 나누어 원래 현의 1/4부분을 퉁겨보면 2옥타브 위의 다음(C²)을 얻게 되고 다른 3/4 부분을 퉁기면 가온 다음의 4도 위 음인 F음을 얻게 된다. 그리고 현을 1:4로 나누어 원래 현의 1/5부분을 퉁겨보면 두옥타브 위의 장3음(E2)을 얻으며 4/5부분은 그냥 장3도(E)에 해당된다. 그리고 똑같은 현을 2:3으로 나누어 3/5부분을 퉁기면 원래 가온 다음의 6도 위 음인 A음을 얻는다.(그림3).

음색 좌우하는 배음들의 합성

피아노의 ‘도’음이나 바이얼린의 ‘도’음은 모두 똑같은 진동수를 가지는 음이다. 그럼에도 불구하고 우리는 두 ‘도’음을 다른 것으로 구별할 수 있다. 음색이 다르기 때문이다. 그렇다면 소리의 음색은 무엇에 의해서 결정될까. 우리가 듣는 피아노의 ‘도’음이나 바이올린의 ‘도’음은 실제로는 하나의 진동수를 가지는 음파에 해당되는 것이 아니라 많은 배음을 지니는 합성파다. 이때 만들어지는 합성파의 모양이 다르면 사람들은 음색이 다르다고 느낀다.

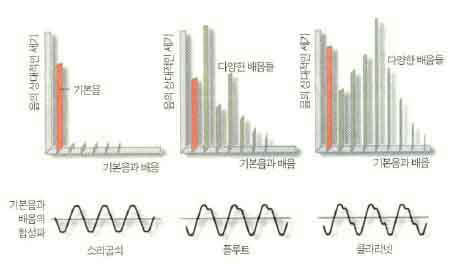
또 똑같은 ‘도’음이라도 그 음이 만들어진 환경에 따라 배음이 섞이는 정도가 다르므로 다른 음색의 음이 만들어진다. 현을 퉁길 때에 발생하는 음파의 진동수는 기본진동수의 정수배가 된다. 따라서 기본진동수가 C음인 현을 퉁기면 그 배음들로 C¹, C² 등의 음들만 생기는 것이 아니라 G¹, E², G² 등 다른 음정에 해당하는 배음들도 함께 생긴다. 이때 배음들이 어떤 상대적인 크기를 가지고 생기는지에 따라서 음의 색깔이 결정된다.

예를 들어 같은 진동수를 내는 소리굽쇠와 플루트 그리고 클라리넷의 배음들을 보면 상대적인 크기가 매우 다른 음들이 섞여있음을 볼 수 있다. 어느 경우에나 기본 진동수는 똑같지만(같은 음정을 내지만) 배음에 있어서는 큰 차이가 있다. 따라서 이들이 중첩돼 나타나는 파의 형태도 조금씩 차이를 보인다. 이것이 바로 여러 악기들의 음색이 달라지는 이유다. 또한 현을 얼마나 세게 퉁기느냐에 따라서도 일반적으로 생기는 배음의 개수가 달라지므로 음의 강약에 따라 미세하나마 음색의 차이가 생긴다. 음색이 여러 배음의 상대적인 강도에 의해서 결정된다고 할 때에 자연계의 소리를 재현하는 것은 쉬운 일이 아니다. 하지만 신시사이저는 한 진동수와 그 배음들을 임의의 강도로 조합해 자연계의 소리와 더불어 다양한 새로운 소리를 만들어낸다.

사람들이 다양한 음색의 음을 얻을 수 있고 또 이 음색의 차이를 구분할 수 있다는 것이 얼마나 다행스러운 일인지 모른다.예를들어 음색의 차이가 전혀 없다면 악기의 구분도 필요없고 교향곡,합주곡(2중주,3중주등)이라는 음악 장르는 애초부터 존재하지 않았을 것이다.또한 가수들의 목소리도 천편일률적으로 같았을테니 음악이라는 것이 얼마나 단조롭고 지겨운 것이 돼 버렸을까.배음들의 합성이 만들어내는 음색의 조화가 세상의 음악을 더욱 풍요롭게 만든다는 사실이 즐겁다.

매질의 진동방향과 파의 진행방향이 나란 공기 소밀의 진동,소리

소리란 공기의 진동,즉 파동이다.파동에는 크게 횡파와 종파가 있다.횡파의 가장 쉬운 예는 수면파다.이 경우 각각의 물분자는 상하 운동을 하지만,물결이 퍼져나가는 방향은 수평 방향이다.이와 같이 매질(수면파의 경우 물)의 진동방향이 파동의 진행방향과 수직인 파동을 횡파라고 한다.반대로 용수철을 좌우로 흔들어줄 때에 용수철의 진동방향은 용수철 밀도의 소한 부분과 밀한 부분이 전파되는 방향과 일치한다.이처럼 매질(용수철)의 진동방향과 파의 진행방향이 나란한 경우를 종파라고 한다.소리는 종파에 해당한다.즉 공기 밀도의 소밀(성김과 빽빽함)이 전파돼 나가는 것이 바로 음파다.

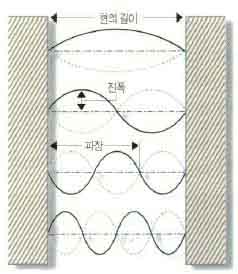
모든 파동은 수학적으로 간단하게 기술된다.예를 들어 수면파를 생각해보자.물결이 일면 물결의 높이와 파장,파동의 모양이 진행해 나가는 속도,물분자의 상하 진동수 등을 생각해볼 수 있다.파의 운동이 공이 시계추의 운동과 비교해서 복잡하게 보이는 이유는 파의 형태가 시간에만 의존하는 것이 아니라 위치에도 의존하기 때문이다.

​여기에서 비롯되는 복잡성을 피하기 위해서 다음과 같은 두경우를 고려해 보는 것이 편하다.우선 시간에 대한 의존도를 없애버리려면 수면파의 모습을 어느 순간 사진에 담았다고 생각하면 된다.시간은 사진을 찍은 순간으로 고정돼 있음에도 불구하고 수면파의 모습은 우리가 잘 아는 골과 마루의연속으로 나타날 것이다.이때 마루와 마루 사이의 수평 거리가 파장이 되고,마루의 높이가 바로 수면파의 진폭이 된다.반대로 수면 위의 고정된 한 점이 시간에 따라 어떻게 상하로 진동하는지를 살펴볼 수 있다.이 경우에는 수면파의 위치 의존도를 잊어버릴 수가 있으며,1초에 몇번 진동하는지가 바로 진동수가 된다.