d라이브러리

수학은 자연의 근원에 이르는 길이자 자연의 아름다움을 보여주는 증거다. 수학에서 볼 수 있는 아름다움은 참으로 많다. 복잡한 숫자들이 하나의 식으로 통합되고 단 하나의 함수로부터 수많은 형태들이 풀려 나온다. 소립자들의 운동을 표현하는 양자역학의 파동방정식이 보여주는 단순함과 명료함은 자연의 복잡성을 단 한줄의 방정식 속에 함축하는 수학적 아름다움의 전형일 것이다.

수학의 전 역사를 통해 자연의 질서와 아름다움을 보여주는 수학의 대표주자로서 많은 수학자들과 일반인들을 매료시킨 것은 마방진이었다. 마방진은 1에서 N제곱까지 모든 숫자들을 한 번씩만 사용해서 N행 N열의 배열을 만들었을 때 어떤 행이나 열이나 대각선의 수를 합해도 항상 합이 같아지는 배열을 말한다. 마방진이라는 말은 영어 magic square를 번역한 말이다. 사각형 모양을 방형이라고 하듯이 사각형 모양의 숫자배열을 ‘방진’이라고 한다. 마방진은 여러 방진들 중에서 상하좌우 대각선의 합이 모두 같은 특수한 조건을 만족하는 ‘마술적인 성질을 가진 방진’이라는 뜻이다.

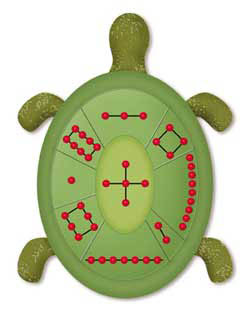
거북 껍질에 새겨진 모양

지금까지 수많은 형태의 마방진이 만들어지고 이를 이론화하려는 연구들이 있었다. 그 중에서도 역사상 가장 먼저 출현한 마방진은 3행3열의 마방진일 것이다. 전설에 따르면 중국 하나라의 우임금이 매년 범람하는 황하의 물길을 정비하던 중에 강에서 이상한 그림이 새겨진 거북의 등껍질을 얻었다. 낙서(洛書)라고 불리는 이 그림에는 1부터 9까지의 숫자가 3행 3열로 배열돼 있는데 어느 방향으로 더하든지 합이 15가 되는 신기한 것이었다. 이때부터 중국에서는 낙서가 세상의 비밀과 진리를 함축하고 있다고 믿었다. 이는 주역의 원리가 함축된 그림으로 인식되기도 했고, 우주의 진리를 표상하는 그림으로 생각됐다. 그만큼 마방진은 보는 사람으로 하여금 신비한 아름다움을 느끼게 한다.

3행 3열의 마방진은 아마도 고대 그리스의 피타고라스 학파나 다른 수학자들에게도 많이 알려져 있었을 것으로 생각된다. 그러나 마방진은 신비한 만큼 비밀스럽게 전수돼서 기록으로 남은 것은 거의 없다. 중국에 전해오는 낙서 이후 유물로 남은 마방진은 뒤러의 4행 4열 마방진이다. 16세기 초 독일의 광석기술자였던 알브레히트 뒤러는 자신의 관뚜껑에 ‘멜란콜리아’라는 4행4열의 마방진을 새겨놓았다. 그리고 이 마방진의 맨 아랫줄 가운데 두칸의 숫자는 15와 14로 이루어져 있었는데, 이를 연속해서 쓰면 그가 죽은 해 1514년을 가리키도록 한 교묘한 방진이었다.

이처럼 마방진은 그 교묘하고 신비함이 글자 그대로 마술적인(magic) 느낌을 갖게 한다. 때문에 마방진은 고대부터 자연철학자들의 관심의 대상이 됐고, 근대의 수학자들도 관심을 가졌다. 17세기 중반 천재수학자 페르마(1601-1665)의 시기까지 수많은 수학자들이 마방진에 매료됐고 연구를 수행했다. 그러나 오일러(1707-1783)와 가우스(1777-1855)에 이르러 흥미가 반감됐고 현대 수학에서도 특별한 관심을 얻지는 못하고 있다. 이것은 마방진이 수많은 연구에도 불구하고 이론화하기가 어렵고 수학의 다른 분야와 연관성을 맺기가 어려운 주제였기 때문이었다. 언뜻 자연수를 다루기 때문에 정수론과 관련되고, 숫자의 조합을 다루므로 조합론에도 맥이 닿고 있지만 피상적인 관련성을 깊이 연결시키는 연구성과는 많지 않다.

간단해서 더 어려운 문제

KAIST 수학과의 한상근 교수에 따르면, 최근 들어 전문수학자들 사이에서 마방진이 연구되면서 고급수학과 관련이 있다는 점이 조금씩 지적되고 있다고 한다. 특히 수학자 알렌 아들러는 방진의 원리를 이론화해서 컴퓨터를 동원해 3차원 입체 마방진을 고안하기도 했다. 그러나 여전히 마방진에 대한 구체적인 연구성과는 아직 많지 않은 실정이다.

수학자들은 마방진 문제가 ‘3X+1 문제’와 같이 보기에는 매우 규칙적이고 간단해 보이지만 완벽하게 이론화하기가 어려운 대표적인 주제라고 말한다. ‘3X+1 문제’는 매우 간단하다. 임의의 수가 있을 때 이것이 홀수이면 그 수에 3배를 해서 1을 더하고, 이것이 짝수이면 이를 반으로 나누는 것이다. 어떤 수가 있을 때 이 규칙을 계속해서 적용하면 끝내는 1일 나오는데 이 간단한 원리가 지니고 있는 수학적인 의미가 현대에도 아직 해소되지 못하고 있다. 예를 들어 7이 있다면, 이 수는 홀수이므로 3X+1을 해서 22가 된다. 22는 짝수이므로 2로 나누어 11이 된다. 11은 34로, 34는 17로 바뀌는 과정을 계속한다. 그 과정은 7-- 22-- 11-- 34-- 17-- 52-- 26-- 13-- 40-- 20-- 10-- 5-- 16-- 8-- 4-- 2-- 1이 된다. 짝수인 4가 있을 때 그 과정은 4--2--1로 돼 처음 수가 홀수이건 짝수이건 모두 끝내는 1이 된다. 이렇게 언뜻 보기에는 간단한 원리를 담고 있지만 이것의 수학적인 의미가 무엇이냐에 대해서는 아직 명쾌한 설명이 나오지 않는다.

마찬가지로 마방진도 상하좌우 대각선의 숫자의 합이 일정하므로 금방 어떤 일반적인 원리가 도출될 것 같지만 이것은 그리 쉬운 일이 아니다. 오죽하면 수천년 동안 수학자들이 관심을 가졌으면서도 명쾌한 답을 못내고 있을까.

지금까지의 연구 결과 2행 2열만 빼고 모든 방진에서 마방진이 존재한다는 것이 알려졌다. 1행 1열(1차 방진)의 방진은 숫자가 1 하나 뿐이므로 자명하게 마방진이 된다. 그런데 2행 2열(2차 방진)의 방진은 마방진이 될 수 없다. 1, 2, 3, 4를 한 번씩만 써서 상하좌우, 대각선 방향의 숫자 합을 같게 할 수가 없다. 3행 3열(3차 방진)의 경우 낙서의 방진에서 보듯이 마방진이 존재한다. 지금까지 밝혀진 바로는 3차 마방진은 낙서의 배열이 유일하다. 4차 방진은 뒤러의 방진에서 보는 것처럼 마방진이 존재한다. 그런데 4차 이상의 방진에는 배열이 다른 마방진들이 여러개 존재하는 것으로 알려졌다. 현대수학자들이 현재까지 알아낸 바로는 4차 마방진은 8백80개, 5차 마방진은 2억7천5백30만5천2백24개가 존재는 것으로 계산됐다. 그러나 6차 이상의 마방진에 대해서는 그 숫자가 몇 개인지 알지 못한다.

탁월한 수학자 최석정

이러한 마방진은 고대 그리스 수학의 전통을 이은 유럽의 수학은 물론 인도수학에서도 많은 논의가 이루어졌다. 또한 중국과 우리나라에서도 예외가 아니었다. 하나라 때의 낙서의 전통을 계승한 주역에 관심을 기울인 유학자들 중 수학에 관심을 가진 많은 사람들이 마방진을 언급했다. 그 중에서도 중국 송나라 때의 양휘라는 수학자는 방진연구에 남다른 애착을 보였다. 그의 책 ‘양휘산법’에서는 당시까지 흩어져 있던 여러가지 방진을 모아놓고 또 자신이 고안한 다양한 형태의 배열그림도 소개하고 있다.

또한 우리나라에서도 방진 연구가 있었는데, 획기적인 공헌을 한 사람은 조선 후기 유학자이자 수학자인 최석정(호는 명곡, 1646-1715)이었다. 그의 책 ‘구수략’에는 3차에서부터 10차까지의 마방진이 서술돼 있는데, 특히 자신이 고안한 9차 마방진은 수학적 탁견을 보여준다. KAIST 수학과 한상근 교수와 대학원생이 공동연구한 결과, 최석정의 9차 마방진은 직교 라틴방진이라는 매우 명쾌한 이론 아래서 이루어진 것으로 그의 수학에 대한 이해와 독창성을 잘 드러내주고 있다. 이 마방진은 9행 9열 대각선의 합이 3백69로 같음은 물론 이를 이루는 9개의 숫자로 이루어진 9개의 작은 셀(cell)이 다시 마방진을 이루는 특이한 구조로 돼 있다.

직교 라틴방진은 종횡으로 숫자가 겹치지 않게 배열하고 이러한 배열 두 쌍을 결합시켰을 때에도 겹치는 숫자쌍이 없는 방진이다. 최석정은 그의 책에서 2개의 9차 마방진을 제시하고 있는데 이를 만들기 위한 기초 작업으로 ‘구구모수변궁양도’(九九母數變宮陽圖)와 ‘구구모수변궁음도’(九九母數變宮陰圖)라고 하는 두 개의 직교 라틴방진을 제시했다. 이름 그대로 이 라틴방진을 ‘어머니 숫자’(모수)로 해 각 순서쌍을 변화시키면(변궁) 마방진이 만들어진다는 것이다. 한상근 교수는 최석정이 직교 라틴방진 뿐만 아니라, 3차 마방진 두 개를 결합해서 9차 방진을 만들어내는 현대수학자 아들러의 연산법도 알고 있었다고 말했다. 최석정은 그는 책에서 “이들은 (내가) 새로 만든 것이다”고 밝히고 있어 그의 수학실력에 경탄을 자아내게 한다.

지수귀문도의 비밀

서양의 경우 마방진처럼 사각형 형태의 직교형 배열에 집중한 것인 반면 동양에서는 방진 외에도 원형, 십자형, 거북등형 등 다양한 형태의 숫자배열에 깊은 관심을 가졌다. 그것은 대표적으로 양휘와 최석정의 책에서 잘 볼 수 있다. 최근 서구에서는 유대 별모양의 6각형 배열, 삼각형 배열, 오각형 별모양 배열 등 다양한 형태의 배열들이 논의되고 있기는 하지만 형태도 단순할 뿐더러 논의의 전통도 그리 길지 못하다.

최석정이 제시한 여러 배열도 중에서 가장 눈길을 끄는 것은 거북등 모양으로 숫자를 배열하는 ‘지수귀문도’(地數龜文圖)이다. 이는 육각형을 벌집모양으로 이어 각 꼭지점에 숫자를 써넣고 하나의 육각형을 이루는 6개의 숫자합이 같도록 하는 배열이다. 그의 책에서 제시된 것은 숫자의 개수가 총 30이고 각 육각형의 합은 93이 되는 교묘한 배열이다. 이러한 모양은 가장 기초적인 6개의 숫자를 배열한 육각형 하나로 이루어진 모양에서부터 16개의 숫자를 배열한 육각형 4개, 30개의 숫자를 배열한 육각형 9개(지수귀문도) 등 여러 모양을 만들 수 있고 배열하는 숫자의 개수에 따라 무한히 확장할 수 있다.

지난 1993년 한상근 교수는 이 지수귀문도를 탐색해보았지만 일반적인 원리를 밝혀내지는 못했다고 한다. 이때 한 석사과정 학생은 지수귀문도에도 6각형의 합이 90이 되는 배열도 만들 수 있다는 것을 알아냈다. 또한 1992년에 지수귀문도의 존재를 모른 채 그래프 이론(Graph Theory)으로 일반적인 6각형 숫자배열을 연구하던 수학자 베카는 6각형의 숫자합이 92가 되는 특수해를 하나 찾아냈다. 종합하면 지수귀문도의 숫자배열은 90, 92, 93이 되는 세가지 형태로 다양할 수 있다는 점이 밝혀진 것이다. 그러나 한상근 교수에 따르면, 90이나 92 등도 배열을 만들 수는 있지만 최석정이 제시한 93의 배열이 가장 안정적이라고 한다. 그것은 30개의 각 꼭지점을 채우는 1에서 30까지의 숫자를 6개 골라냈을 때 기대값이 93이라는 사실로부터 얻어진 것이었다. 한교수는 이후 이 지수귀문도에 더 이상 매달리지 못하고 잊고 있었다.

그런데 10여년 전 신문광고에 우연히 나온 지수귀문도를 보고 호기심이 발동한 지용기씨(34세, 개인사업)는 밤을 새워가며 독자적으로 새로운 배열을 만들어낼 수 있었다. 그는 최근까지 이 지수귀문도를 더욱 확장해 숫자의 개수가 6, 16, 30, 48, 70, 96, 126 등으로 만들어지는 다양한 크기의 지수귀문도를 완성할 수 있었다. 또한 수의 개수가 많아지는데 따라 합이 변하는 규칙성도 알아냈다. 그러나 그는 끝내 이러한 숫자배열을 완성시키는 일반적인 방법에는 도달하지 못했다.

현대수학자의 과제

한편 지수귀문도를 완성한 지용기씨의 보도를 일간 신문을 통해 접한 이지원씨(33세, 한국기초 과학지원연구원 생체고분자실)는 자신이 이미 10년 전에 지수귀문도를 완성하는 일반적인 방법을 고안했다고 한상근 교수를 통해 알려왔다. 이씨의 원리는 너무도 간단해서 이씨 자신도 처음에는 "별로 대단한 것이 아니다"고 던져두었던 것이다. 이를 검토한 한상근 교수는 "매우 간편하고 명료해서 수학적인 일반화가 가능할 것이다"고 반겼다.

이지원씨의 방법에서 특기할 만한 것은 숫자의 배열을 바꿀 경우 육각형의 합이 여러 값으로 나오는 것을 설명할 수 있다는 점이다. 이지원씨는 이미 30개의 숫자로 배열을 만들 경우 89, 91, 95, 97 등 다양한 값으로 나타나는 배열도 완성했다. 이는 합이 93이었던 최석정과 지용기씨의 방법과는 약간 차이가 나고 당연히 배열방식도 다른 것이다.

이지원씨의 방법에서 또하나 특기할 점은 합을 만들어가는 방법이 너무나 명쾌하고 간단해 초등학생도 이해할 정도라는 것이다. 한상근 교수는 "전문 수학자가 조금 더 고민해보면 일반식을 만들 수 있을 것이다"고 말했다. 또한 지금까지 나온 합이 조금씩 다른 지수귀문도의 배열들을 종합해 볼 때 아마도 마방진과 마찬가지로 지수귀문도도 합이 같다고 하더라도 배열이 여러가지일 수 있다. 더욱이 형태는 같더라도 여러 종류의 합이 나올 수 있어서 여기에서 풀려나오는 비밀스런 배열의 개수가 얼마나 될 것인지, 왜 이런 성절이 나타나는지에 대해 더욱 깊이 있는 연구가 필요한 실정이다.

고대부터 서양에서는 수를 아름다움의 상징으로, 동양에서는 세상의 진리에 이르는 길로 생각해왔다. 그것은 많은 사람들이 숫자들 속에 우리가 간파하지 못하는 신비한 규칙성과 조화가 숨어있다는 것을 알아차린 때문이었다. 그러나 아직도 우리는 그 신비한 성질이 무엇으로부터 비롯되는 것인지, 우리가 감질나게 느끼고 있는 수학적 아름다움의 실체가 무엇인지는 여전히 베일에 싸여있다. 수천년을 두고도 해명되지 않는 숫자의 신비와 배열의 오묘함을 이제 현대수학이 한번 해명해야할 때가 된 것 같다.

쉽게 만들어보는 마방진

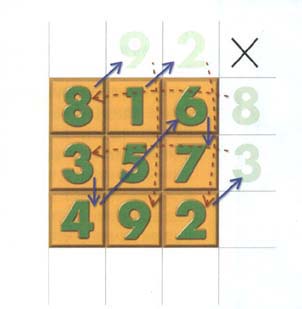
① 홀수 차수 방진 - 대각선법

만들고자 차수의 방진을 그리고 그 외부에 한 칸씩을 더 그린다. 맨 윗줄 중앙 칸을 1로부터 시작해 대각선으로 순서대로 숫자를 써 나간다. 바깥쪽 칸에 쓰여지는 숫자는 다시 반대편 칸에 이동해 채우고 이어서 대각선으로 계속 숫자를 써 나간다. 대각선이 이미 차 있으면 아래로 한 칸 내려쓰고 계속한다. 이 방법으로 모든 홀수차수 방진에서 마방진을 만들 수 있다.

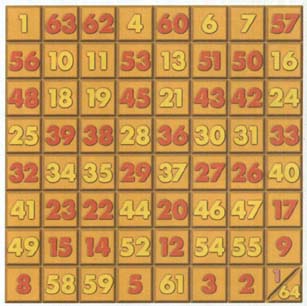
② 2의 거듭제곱 차수 방진(4, 8, 16, 32······) - 모스-헤드룬트수열법

이 수열은 0과 1만 사용해서 1부터 시작해서 다음 항은 그 항까지의 0과 1 숫자 배열을 거꾸로 하는 것이다. 0은 1로 1은 0으로. 이 수열을 항별로 나열해보면 1 0 01 0110 01101001 0110100110010110 0110100110010110100101100110100101101001····로 나타난다.
이 수열의 0과 1의 배열을 ${2}^{n}$차수의 방진의 각 칸에 맨 왼쪽위에서 부터 차례로 채워나간다. 그런 다음 0과 1이 있는 곳을 구별해서 맨 왼쪽 윗칸에서 시작해 1부터 숫자를 채워나간다. 1에 해당하는 곳에는 순서대로 수를 쓰고 0이 있는 곳은 건너뛴다. 끝까지 다 갔으면 이번에는 끝에서 부터 다시 0이 있는 자리에 순서대로 숫자를 채워나간다.

③ 2x홀수 차수 방진 - LUX법

이 방법은 콘웨이가 개발한 방법으로 6차, 10차 등의 짝수방진을 만들 수 있다. 숫자를 매겨나가는 방식이 2행 2열의 방진에서 L,U,X형태의 세가지 패턴을 사용하므로 LUX법이라고 이름 붙였다. L,U,X를 정하는 방법은 따로 마련된 규칙을 따른다.

위의 세가지를 종합하면 2행2열의 2차 방진을 제외한 모든 차수의 방진에서 마방진을 만들 수 있다. 그러나 어느 차수의 방진이 몇 개의 마방진을 갖는가 하는 문제는 아직도 풀지 못하고 있다. 지금까지 알려진 바로는 3차 마방진은 1개, 4차 마방진은 8백80개, 5차 마방진은 2억7천5백30만5천2백24개이고, 6차 이상은 개수를 모른다.

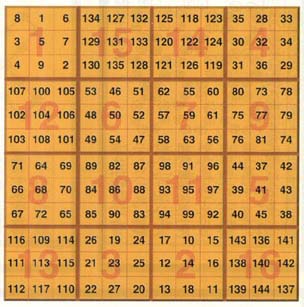
④ 마방진 2개로 새로운 마방진을 만드는 방법 - 아들러의 연산법

이미 알고 있는 마방진 2개를 결합해 새로운 차수의 마방진을 만들 수 있다. 그림은 3차 방진과 4차 방진을 결합해서 12차의 방진을 만드는 과정을 보여준다.
4차 방진의 숫자에 해당하는 칸에 3차방진을 배열해 넣는다. 4차 방진 내의 해당 숫자만큼 배가된 3차 방진을 넣으면 된다.