d라이브러리

서커스장에 가면, 공이나 유리병 같은 것을 빙글빙글 돌리는 재주꾼들을 자주 볼 수 있다. 그런데 요즘은 컴퓨터오락, 게임기 같은 놀이가 등장해 옛 놀이를 몰아내는 것 같아 안타깝다. 반세기 전만 하더라도 어린이들이 즐기던 놀이 중의 하나가 집에서 정성들여 만든 콩주머니 몇 개를 이 손에서 저 손으로 빙글빙글 돌리는 것이었다. 이러한 재주를 돌리기 재주, 저글(juggle)이라고 부른다.

수학자들이 음악이나 주역, 점성술, 장기, 바둑 같은 것을 수학적으로 해석하는데 관심을 가진 것은 아주 오래 전부터이다. 이미 피타고라스(B.C. 572-492)는 세 현이 만드는 음이 아름답게 조화를 이루려면, 그 길이가 조화수열을 이루어야 한다는 것을 발견했다. 또 10세기 바그다드의 저잣거리에서 유리병을 돌린 아부 자알(Abu Sahl)은 문헌에 기록된 ‘최초의 저글하는 수학자’ 였다.

최근 저글은 ‘자리 바꿈 기호’ 라는 수학적 이론을 갖게 됐다. 이 연구로 기존의 저글 방법들이 체계적으로 설명되었을 뿐 아니라, 지금까지 재주꾼들에 의해 행해진 적이 없던 새로운 저글 방법이 무수히 많이 발견됐다. 이 이론에 따르면 어떤 하나의 저글방법은 수열로 표현된다. 또 어떠한 수열이 몇 개의 공을 갖고, 어떤 방식으로 저글을 할 수 있는가를 알려준다.

실제로 저글재주꾼이 ‘자리 바꿈 기호 이론’ 으로 나타내는 저글방법을 묘기로 보이는 것이 쉬운 일은 아니다. 그래서 최근에는 미리 어떻게 돌리기를 할 수 있는지를 컴퓨터 프로그램을 통해 볼 수 있는데, 인터넷에서 다양한 저글게임을 얻을 수 있다(URL : http://www.juggling.org).

저글을 하는 데에는 달걀, 사과, 우산, 횃불, 접시, 고리, 빗자루, 망치, 전기톱 등 여러가지가 쓰일 수 있지만 편의상 공을 던지는 것으로 생각하자. 이론적으로는 한없이 많은 공을 던지고 돌리고 할 수 있지만, 여기서는 유한개의 공을 가지고, 일정한 형을 반복하는 주기적인 저글에 대해 알아보기로 하자. 실제로 사람이 다룰 수 있는 공의 개수는 10여개 정도다.

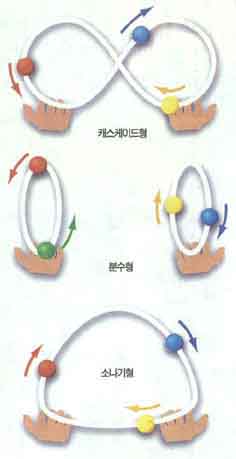
저글에는 세가지 기본형이 있다. 첫째는 캐스케이드(cascade), 즉 ‘계단식 폭포’라고 불리는 것. 오른손이 던진 공을 왼손이 받고, 왼손은 이것을 다시 오른손으로 보낸다. 세개 혹은 홀수개의 공으로 8자를 눕혀놓은 ‘무한대 기호’(∞)모양으로 공을 돌린다. 캐스케이드는 짝수개의 공으로 실행할 수 없다. 짝수개를 돌리면 공들이 중간에서 부딛치기 때문이다. 1993년에 열린 국제 저글꾼 대회에서 가토(A. Gatto)라는 재주꾼은 9개 공으로 캐스케이드 던지기를 무려 60회 이상 해, 세계 신기록을 세웠다.

두번째 기본형은 분수(fountain)형이다. 분수형은 공들이 손을 바꾸지 않고 도는 것을 말한다.(그림1) 이탈리아의 라스텔리(E. Rastelli, 1896-1931)는 10개의 공으로 분수형 던지기를 20회 실행하기도 했다.

마지막으로 소나기형(shower)이 있다. 이것은 공을 오른손에서 왼손으로 큰 포물선을 그리면서 던진 다음, 다시 왼손에서 오른손으로 낮게 던지는 것이다.(그림1) 오른손이 먼저 시작하느냐, 왼손이 먼저 시작하느냐는 별로 중요하지 않다.
 

새로운 묘기도 예측가능

위의 세가지 기본형을 자리 바꿈 기호로 표현하면,

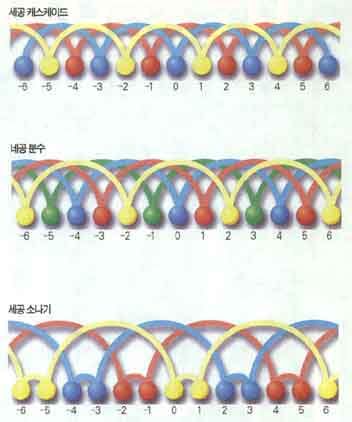
세공 캐스케이드형 = 3
네공 분수형 = 4
세공 소나기형 = 15
가 된다. 어떻게 이런 숫자들이 나오게 됐을까.

자리바꿈기호 3, 4, 15 라는 숫자는 공의 개수, 박자, 주기의 종류를 결정한다. 우선 공의 개수는 3/1 = 3, 4/1=4, (1+5)/2 = 3 으로 계산한다. 즉 각 자릿수 숫자의 합을 자릿수로 나누면 공의 개수가 나온다. 한편 3은 세박자, 4는 네박자를 주기로 공을 돌린다는 것이다. 그럼 15는? 원래 열다섯박자의 주기를 가진다는 표시지만, 열다섯박자로 공돌리기는 불가능하므로, 한박자와 다섯박자의 두가지 종류의 주기를 갖고 공을 돌린다는 표시다.

여기서 홀수는 한 손에서 다른 손으로 보내는 것을 뜻하고, 짝수는 던진 손으로 다시 공을 받는 것이다. 1은 한 손에서 다른 손으로 잽싸게 보내는 것, 2는 손에 있는 공을 살짝 던지고 나서 던졌던 손으로 다시 받는 것을 뜻한다. 실제적으로는 공을 가만히 들고 있어도 된다.

다시 정리하면 자연수 n이 뜻하는 바는 이 공이 n박자 후에 다시 던져진다는 것을 의미하고, 이때 n이 홀이냐 짝이냐가 다른 손으로 던져지느냐 아니면 같은 손으로 던져지느냐를 결정한다. 물론 n이 크면 클수록 높이 던져야 한다. 기호 0은 빈손을 뜻한다.

그렇다면 3이라는 기호는 던진 공이 3박자 후에 다른 손에서 다시 던져지는데 매 박자마다 계속 반복된다. 즉 3333…이 연속되므로 ‘세공 캐스케이드’다. 이 재주를 익히려면, ‘꿍작작 꿍작작’의 세 박자에 맞춰 던지는 연습을 하면 된다.(그림2)

마찬가지로 4는 던진 공이 네 박자 후에 다시 같은 손에 의해 던져지는 것이므로, 네개의 공으로 양손이 번갈아 가면서 두 개의 공을 돌리는 재주, 즉 ‘네공 분수’가 된다.

마지막으로 15는 원래 (1,5)라고 했으므로, 1에 의해 왼손에 잡은 공을 오른손으로 재빨리 보내고, 다시 이 공을 오른손이 높이 던져 5박자 후에 왼손으로 잡을수 있게 하라는 표시다. 다섯박자 공은 세박자 공보다 두배 정도 더 높이 던져야 한다. 기호 15는 15가 계속 반복되는 수열 151515… 를 뜻한다. 15나 51은 두가지 박자를 갖고 공을 던지므로 ‘소나기’ 저글이다. 15는 세 개의 공이 필요하므로 ‘세공 소나기’저글이다.

공돌리는 로봇

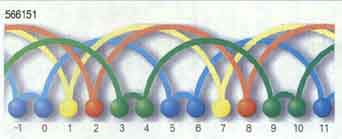
자리 바꿈 기호 이론은 재주꾼들이 “다음 공을 어떻게 처리할까?”라는 걱정보다는 “지금 던지는 공은 어떻게 던져야 하는가?”만 고민하도록 도와줬다. 이제 재주꾼들도 알아보기 힘든 자리바꿈기호 566151이 나타내는 저글이 어떤 것인지 살펴보자. 주어진 수열을 더하고 자리수로 나누면 공의 개수가 나온다. 즉 ‘저글 566151’은 (5+6+6+1+5+1)/6 = 4 개의 공으로 하는 재주가 된다. 또 공들은 다섯박자, 여섯박자, 여섯박자, 한박자, 다섯박자, 한박자의 6가지 주기를 갖고 돈다는 것을 알 수 있다.

수학자 불러가 만든 이론에 따라 수열 566151가 실제로 저글이 가능한가를 판정하는 방법은 다음과 같다. 각 자리수에 0,1,2,3,4,5 를 각각 더한다(578496). 이때 6이상의 수들은 6으로 나눈 나머지로 바꾼다(512430). 만약 이 수열이 012345를 자리바꿈해 얻어질 수 있다면 그 수열은 실행가능한 저글이다(이런 방법을 0,1,2,3,4,5 치환이라고 부른다). 이러한 판정법을 역으로 시행하면, 자리 바꿈 기호를 얻게 된다.

불러는 b개 미만의 공으로, 주기가 p인 저글의 가짓수는 ${b}^{p}$이 된다는 것을 밝혔다. 즉 5개 미만의 공으로, 주기가 4인 저글의 가짓수는 5⁴, 즉 6백25 가지나 된다. 또 b개의 공으로 주기가 p인 저글의 가짓수에 대한 공식도 나왔는데, 234, 504, 345, 5551, 40141, 561, 633, 55514, 7562, 7531, 566151, 561, 663, 771, 744, 753, 426, 459, 9559, 831 등이 있다. 불러 이론에 따르면 저글은 반드시 두손으로 할 필요도 없다.

이렇게 이론들이 제시하는 새로운 저글법을 재주꾼들이 익히고 묘기를 보여주는 것은 또 다른 문제다. 최근 IBM의 도너(M. Donner), 예일대학의 코딧섹(D. Koditschek)같은 공학자들에 의해 저글을 할 수 있는 로봇을 개발하려는 시도가 활발히 진행되고 있으나, 의외로 발생하는 카오스적인 현상이 저글 로봇 탄생을 방해하고 있다. 저글 로봇은 자유운동을 제어하는 로봇 개발에 매우 유용하다. 쓰레기를 청소차에 던지는 로봇, 보도블록을 까는 로봇, 물밑에서 용접하는 로봇 등의 개발과도 관련이 있다. 하지만 남대문 시장에서 저글하는 로봇을 구경하기는 아직 이른 것 같다.