d라이브러리

갈릴레이가 발견한 단진동은 일상생활에서 널리 활용되는 주기운동이다. 현실의 세계에서 벗어나 지구중력을 이용한 단진동 땅굴열차를 상상해보자.

 갈릴레이가 피사의 사원에서 램프가 바람에 흔들리는 것을 보고 발견했다는 '진자의 등시성'이라는 것이 있다. 즉 램프의 무게가 가벼우나 무거우나 한번 갔다오는데 걸린 시간(주기)은 같고, 심지어 많이 흔들리든 적게 흔들리든 주기는 변하지 않는다는 것이다. 흔들리는 정도를 나타내는 물리량을 진폭이라고 하는데 진폭이 크면 빠르고, 진폭이 작으면 느리게 움직여서 결국 한번 움직이는데 걸리는 시간이 같다는 것이다.

바람에 흔들리는 램프, 시계추의 운동, 추가 달린 용수철의 운동… 등과 같이 주기적으로 왕복운동하는 것을 단진동이라 한다. 단진동운동의 특징은 일정한 범위에서 같은 운동을 반복하면서, 진동의 중심을 지날 때에는 속도가 가장 빠르고 끝으로 갈수록 속도가 줄어서 끝에서는 정지하고 운동의 방향이 바뀌면서 다시 진동의 중심으로 가면서 속도가 점점 증가한다.

이는 진동의 중심으로부터 작용하는 힘이 있어서 추가 밖으로 벗어나려는 것을 중심으로 당기는 힘이 작용하는 것처럼 보인다. 이를 '복원력'이라고 한다. 복원력은 항상 추가 움직이는 중심방향으로 작용하며 진동의 중심에서 멀어질수록 그 힘이 커진다.
 

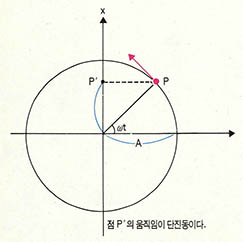
원운동의 그림자

일반적으로 단진동의 정의는 원운동의 그림자운동이다. 지금 어떠한 물체가 수평방향으로 등속으로 원운동하고 있다고 가정하자, 이 물체를 수평방향에서 보면 좌우로 왕복운동한다는 것을 알수 있다. 이 방향에서는 앞뒤가 구별이 안되기 때문이다. 지금 어떤 물체 P가 반경 A인 원주위를 따라 시계반대방향으로 각속도 ω로 등속원운동하는 물체가 있을 때 t초 후에는 ωt만큼 회전할 것이고 이 물체의 원점으로부터의
거리 x=Asinωt 거리를 시간으로 나누면(미분하면) 속도가 되므로

속도 v=x'=Aωcosωt
또 속도를 시간으로 나누면(미분하면) 가속도가 되므로

가속도 a=v'=-A${ω}^{2}$sinωt=-2x

따라서 단진동을 일으키는 힘은 가속도에다 추의 질량을 곱해야 한다. 복원력 F=ma=-m${ω}^{2}$x가 되어 복원력의 일반적인 형태인 거리에 비례하는 힘이 반대로 작용하는 것을 나타낸다.

단진동에 대한 일반식을 가지고 진자의 등시성을 설명해보기로 하자. 램프를 흔들리게 하는 복원력은 램프에 작용하는 중력의 진동중심방향 성분이며 이는 램프의 질량을 m, 진자의 길이를 ℓ 이라 할 때 진폭이 충분히 작다는 전제하에서(진폭이 크면 진자의 등시성은 성립하지 않는다) 복원력 F=-mgx/ℓ이고 이것이 복원력의 일반식 -m${ω}^{2}$x와 같아야 하므로 2=g/ℓ이다.

ω=2π/T 이므로 주기 T=2π${(ℓ/g)}^{1/2}$이다. 그러므로 진자의 주기는 추의 질량 m과 진폭 x에 무관하며 추의 길이와 중력가속도만이 관계가 있다. 추의 길이가 4배가 되면 주기는 2배가 되어 느려지고 추의 길이가 10배가 되면 주기는 약 3배가 되어 더욱 느려진다. 그리고 중력가속도가 4배가 되면 주기는 반으로 줄어 두배로 빨라지며 중력이 지구의 1/6인 달에서는 주기가 약 2.5배 길어지므로 추시계를 달에 가져가면 시간이 같은 정도로 느리게 갈 것이다.

한편 용수철을 당겼다 놓으면 단진동 운동하는데 이를 단진동시키는 힘은 용수철에 작용하는 복원력이다. 용수철은 처음에 당길 때는 별로 힘이 들지 않지만 많이 늘어날수록 점점 더 힘이 든다. 이를 후크의 법칙이라고 하는데 이를 좀더 유식하게 표현하면 "용수철에 작용하는 힘은 용수철의 변형된 길이에 비례한다"가 되고, 이를 수학적으로 표현하면 F=-kx가 되므로, 변위에 비례하는 힘이 반대로 작용한다는 복원력의 일반식을 만족한다. 여기서 k는 용수철 상수로 용수철의 상태에 따라 달라지는 상수이다. 용수철이 빡빡할 때는 k값이 크고, 느슨할 때는 작게 나타난다.

용수철 상수가 k인 용수철에 질량 m인 추를 달아 살짝 움직였다 놓으면 용수철의 복원력에 의해 단진동운동하게 되고 복원력 F=-kx=-m${ω}^{2}$x에서 ${ω}^{2}$=k/m이다. 따라서 용수철진자의 주기 T=2π/ω=2π${(m/k)}^{1/2}$이므로 역시 진폭에 무관하며 질량과 용수철의 탄성계수에 관계가 있다. 질량이 4배가 되면 주기가 2배가 되어 느려지고 용수철의 탄성계수가 4배가 되면 주기가 반으로 줄어 진자는 두 배나 빠르게 운동한다.
 

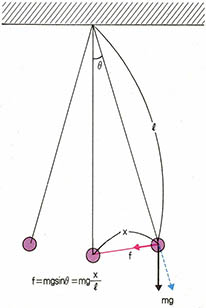
지구를 관통하는 굴에 돌을 떨어뜨리면

땅을 파고 또 파고 계속 파 들어가면 지구는 둥글기 때문에 마침내 지구의 반대편으로 뚫고 나올 것이다. 서울에서 그런 작업을 했다면 서울의 반대쪽인 남아메리카의 아르헨티나가 나온다.

이 바닥이 없는 우물에 돌을 떨어 뜨리면 그 돌은 어떤 운동을 할 것인가? 바닥이 없으니까 아래로 쭉 빠져 버릴까? 그렇지 않다. 지구의 중력에 의해 돌이 떨어지는데 중력은 지구의 중심방향이다. 따라서 지구의 중심까지는 돌의 속력이 점점 빨라지다가 중심을 지나면 올라가는 것이 되어 속력이 점점 줄어들게 된다. 지구의 중심으로 갈 때는 중력과 같은 방향이 되어 속력이 증가하지만 중심을 통과하면 중력과 반대방향이 되어 속력이 감소하여 지구의 반대편 표면에 왔을 때 속력이 0이 된다. 그 돌을 그대로 놔 두면 다시 아래로 낙하하기 시작하여 중심을 통과하여 원래의 위치로 돌아올 것이며 공기의 저항이 없다면 그와 같은 왕복운동을 끝없이 반복할 것이다.

그러면 공기의 저항이 있는 경우에는 어떻게 될까? 천장에 매달린 추가 시간이 지남에 따라 진동의 폭이 점점 줄어 마침내 정지하는 것처럼, 이 바닥이 없는 우물에서 왕복운동하는 돌도 공기의 저항 때문에 진동의 폭이 줄어 결국은 지구의 중심에서 정지하게 될 것이다.

이 돌의 운동이 단진동 운동의 여러 조건을 만족하는 것처럼 보이는데 복원력을 구하여 복원력의 일반식과 비교해 보기로 하자. 이 돌을 왕복운동하게 하는 힘은 명백히 지구의 중력이다. 돌이 지구의 표면에 있을 때는 지구의 모든 질량이 이 돌을 당기는데 영향을 미칠 것이지만 돌이 땅 속에 들어갈수록 이 돌을 당기는데 영향을 주는 지구의 질량은 줄어든다. 구체적으로는 돌의 아래쪽에 있는 지구의 질량만이 돌을 당기는데 기여를 하기 때문에 돌이 지구의 중심으로 접근할수록 당기는 힘은 점점 줄어들고 중심에 도달되면 당기는 힘은 0이다.

지구의 반경을 R 질량을 M이라고 하고 이 돌이 지구의 중심으로부터 x만큼 떨어져 있을 경우에 이 돌에 작용하는 만유인력은 반경이 x인 질량만이 이 돌에 중력을 미친다. 지구의 질량이 균일하다면 질량은 부피에 비례하고 구의 부피는 반경의 세제곱에 비례하므로 반경이 x인 구의 질량은 ${(x/R)}^{3}$M이다. 따라서 이 돌에 작용하는 중력은 만유인력의 법칙에 의해 (GmM/${R}^{3}$)x이 되어 복원력의 일반식을 만족한다.

복원력 m${ω}^{2}$x=(GmM/${R}^{3}$)x 이므로 ${ω}^{2}$=GM/${R}^{3}$이다. 따라서 주기 T=2πR${(R/GM)}^{ 1/2}$가 되고 원주율 π=3.14, 지구반경 R=6.4×${10}^{6}$m, 만유인력상수 G=6.7×${10}^{-11}$N㎡/${kg}^{2}$, 지구의 질량 M=6×${10}^{24}$kg를 대입하면 주기 T는 약 5천초, 1시간 24분이 된다. 즉 바닥이 없는 우물에 돌을 떨어뜨리면 지구의 반대쪽으로 가는데 약 42분이 걸리고 다시 42분이 지나면 원래의 위치로 돌아온다.

흥미있는 사실은, 주기에 영향을 주는 요소가 지구의 질량과 반경인 것 같으나 사실은 지구의 밀도에만 관계있다는 것이다. 2ω= GM/${R}^{3}$에서 지구의 부피는 4π${R}^{3}$/3 이므로 지구의 밀도를 ρ라고 할 때 밀도는 질량을 부피로 나누어 p=3M/4π${R}^{3}$이므로 M/${R}^{3}$=4πρ이어서 천체의 질량이 작으나 크나에 관계없이 오직 밀도만이 주기에 영향을 준다.

목성과 토성에 똑같은 굴을 봤다면 목성이 토성보다 훨씬 크지만 토성의 밀도보다 목성의 밀도가 커서 주기는 더 짧을 것이다.

이 모든 계산이 공기의 저항이 없고, 지구가 자전하지 않는 균일한 밀도의 완전한 구(球)라는 것을 전제로 한다. 실제로는 공기의 저항에 의해서 떨어진 만큼 올라갈 수 없으므로 지구의 반대편 훨씬 못미친 곳에서 되돌아 오게 될 것이고 시간도 더 걸릴 것이다. 또 지구의 자전은 지구상에 있는 모든 물체를 같은 각속도로 서에서 동으로 이동시키기 때문에 낙하하는 물체가 지구의 중심으로 접근함에 따라서 동쪽 벽에 부딪히면서 낙하하게 될 것이다.

함께 생각합시다

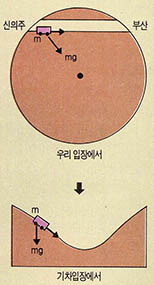
신의주와 부산 사이에 그림과 같이 기하학적 최단거리로 터널을 뚫고 지하철을 건설한다면 어떤 것들을 고려하여야 하는가를 생각해 보자.

도움말

이러한 터널을 만들수만 있다면 이 터널에서 달리는 기차는 동력이 필요 없을 것이다. 우리가 보면 직선코스인 것 같으나 이 기차의 입장에서는 터널 중간까지는 내리막길이고, 중간을 통과한 직후에는 오르막길이다.

내리막의 경사와 길이가 오르막의 경사와 길이가 완전히 같기 때문에 공기의 마찰만 무시하면 이 기차는 두 도시를 왕복운동하게 될 것이다. 실제로는 공기의 저항이 있으므로 그 저항으로 인한 에너지의 손실분만 보충해주면 상당히 효율적으로 물자와 인원을 수송할 수 있을 것이다.

이 터널은 서울에서 신의주쪽으로 직접 빛을 보낼 수 있을 것이지만 터널의 내부에서 새는 물은 터널의 가운데로 흘러 터널의 가운데 공간을 막을 가능성이 있으므로 방수에 가장 신경을 써서 설계를 해야 할 것이다.

본문의 정량적인 계산을 이해한 사람은 이 경우에도 복원력이 지구의 중심을 관통했을 경우와 완전히 같은 형태를 가지며 따라서 주기도 1시간 24분으로 같다는 것을 유도할 수 있을 것이다.