d라이브러리

둥근 지구를 평면에 표시한 지도는 몇가지 점에서 주의를 기울여 살펴야 한다. 여러 목적에 두루 맞는 지도란 없기 때문인데….

우리는 일상생활에서 여러 목적으로 다양한 지도를 사용하고 있다. 어느 국가나 대륙의 위치를 알아보기 위해 참고하는 세계지도는 친구집을 찾아 가거나 여행할 때 사용하는 도로지도와 다르다.

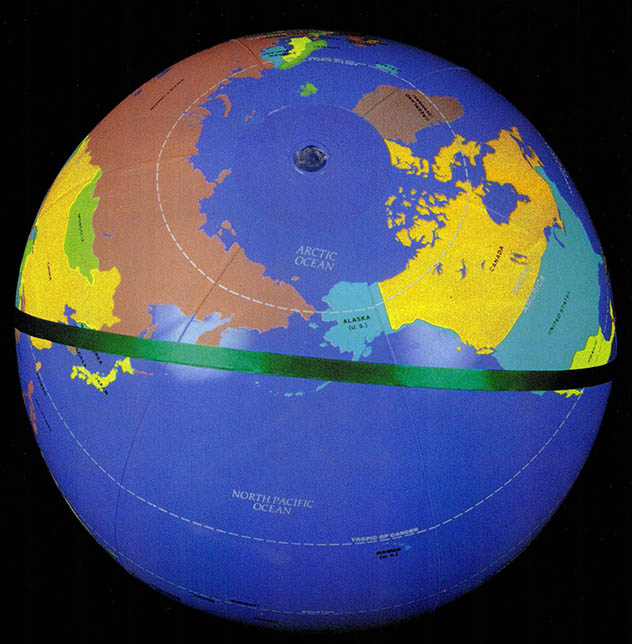
지구의 실제 모양을 축소한 지구의(地球儀)는 지도책이나 한 장의 지도보다 우리에게 훨씬 더 실감을 준다. 이것은 지구의가 지도가 갖추어야 할 방향(방위) 거리 크기 모양의 4가지 특성을 가장 잘 나타내주기 때문이다. 그러나 지구의는 전세계를 한눈에 볼 수 없어서 이리저리 돌려 보아야 하며, 갖고 다니거나 보관도 불편하다는 단점을 가지고 있다. 지구의가 야구공만한 크기라면 이러한 불편은 줄어들겠지만 이 정도의 작은 크기로는 쓸모가 없어지고 만다. 중·고등학교 지리부도에서 흔히 두 페이지에 걸쳐 있는 우리나라 전도(全圖)의 크기라면 직경 4.2m가 넘는 지구의가 필요하다.

둥근 지구를 평면에

지구의가 가진 문제는 한장의 종이에 지도를 그리면 해결된다. 그러나 둥근 지구를 평면에 그대로 나타내려면 지구의 표면이 곡선으로 이루어졌기 때문에 또 다른 문제가 나타난다. 즉 평면에 옮길 때 늘어나는 부분도 있고 또 찢어지는 부분도 생긴다. 이러한 일그러짐은 지도의 특성에 따라 구분해서 살펴볼 필요가 있다.

평면지도는 지구의에 있는 임의의 두 점 사이 거리를 그대로 유지하기 어렵다. 이로 인해서, 지구의에서 두 직선이 만나 생기는 각(角)은 평면에서처럼 유지될 수 없기 때문에 모양이 일그러지며, 면적은 두 지점간의 거리에 비례하기 때문에 지구의에 표시된 일정한 면적이 평면지도에서는 확대되거나 축소되는 두가지 문제가 발생하는 것이다.

이같은 각도와 크기의 문제는 지도상에서 각도를 다르게 하더라도 크기를 상대적으로 같게 하거나 또는 크기는 다르더라도 각도 관계를 지구의에서와 같이 유지해 처리하고 있다. 둥근면을 평면으로 투영할 때 지도의 4가지 특성이 모두 실제와 같게 할 수는 없으나 도법에 따라서는 한가지, 또는 두가지의 특성을 실제와 같이 하고 나머지 특성은 무시할 수 있다. 예를 들면 크기(면적)가 크게 확대되고 방향이 맞지 않더라도 모양은 실제와 같게 할 수 있는 도법이 있고 이와는 반대로 모양은 일그러지더라도 면적을 갖게 할 수도 있다.

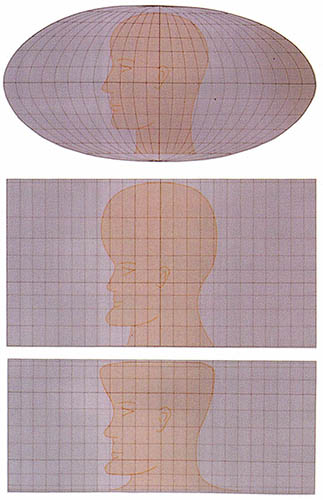
지구의에 표시된 모든 경선과 위선은 서로 직각으로 만난다. 이 관계가 한 장의 지도에서도 유지될 경우 지구의에 있는 임의의 직각관계는 지도에서도 같게 나타나는데, 이런 특성의 도법을 정각(正角) 도법이라 한다.

정각 관계를 유지하면 비록 크기는 확대돼 서로 달라지더라도 모양은 닮은 꼴이 된다. 이러한 닮은 꼴, 즉 정각 특성은 임의의 한 점에 대해서 성립된 것이어서 비교적 좁은 지역에서만 적용된다. 왜냐하면 한 점에서부터 거리가 멀어짐에 따라 축척 또는 점차 커지게 되므로 넓은 면적에서는 지구의와 지도에서 닮은 꼴이 유지될 수 없기 때문이다(그림 1).
 

'비교적' 바른 모양의 메르카토르 도법
 

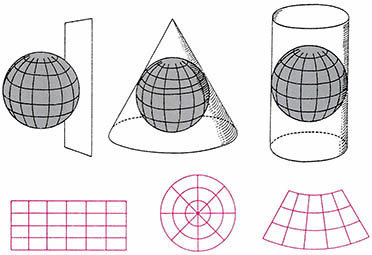
도법이란 둥근 지구의의 표면을 평면으로 나타내는 방법으로, 여기에는 수많은 종류가 있다. 그러나 이들은 투영 원리에 따라 크게 원통도법 원추도법 방위도법의 3가지로 분류된다. 물론 이들 도법의 이름은 편의상 사용하는 것이고 좀더 정확하게는 '원통도법과 관련된 도법' 등으로 표현해야 할 것이다.

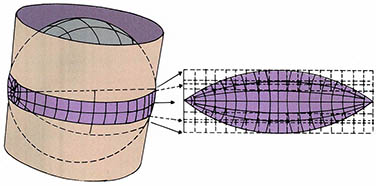
(그림 2)는 도법의 원리를 간단히 표시한 것으로 종이를 원통이나 원뿔, 또는 평면으로 지구의에 접했을 때 지구의의 경위선망이 평평한 종이에 어떻게 투영(지구의가 투명한 플라스틱이나 유리로 되어있고 그 중심에서 촛불이나 전등불을 비추었다고 가정할 때 경위선망이 종이에 비춰지는 것)되는가를 보여준다. 이들 각각의 경우는 광원이 지구의의 중심에 있을 수도 있고 표면에 있을 수도 있으며 지구의로부터 무한대의 거리에 있을 수도 있다.

지도투영법이란 말은 투영원리에서 비롯된 것이며 오늘날은 투영법보다는 도법이라는 용어를 더 많이 사용한다. 그러나 이와같은 투영의 방식으로 지도를 만드는 일은 없고 실제로 지도를 제작하는데는 수학적인 계산에 의해 경위선망을 작성한다. 오늘날 지도투영법이란 말은 알맞지 않으나 지도의 경위선망이 그려지는 근본원리를 이해하는데는 큰 도움을 주고 있다.

도법의 특성에 따라서는 면적이 비교적 정확하게 나타나는 정적도법, 방위를 바르게 나타내는 방위도법 등으로 분류가 가능하지만 이 역시 편의를 위한 대분류에 불과하다.
 

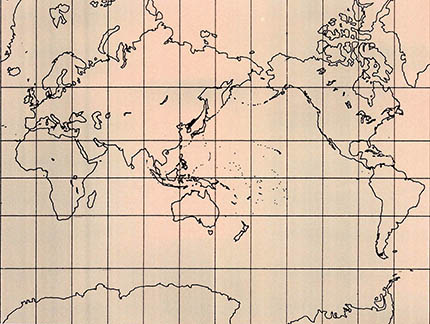
정각도법의 세계지도로 가장 널리 알려진 도법은 1569년 프랑스의 메르카토르에 의해 만들어진 메르카토르도법이다(그림 3). 이 도법이 널리 사용되는 이유는 어떤 국가나 지역의 모양이 일그러짐 없이 비교적 바르게 지도에 표시되며, 항해 기술이 크게 발달하지 못했을 당시 두 지점간을 동일한 방위각으로 항해하도록 하는 장점을 가진 정각도법이라는데 있다.
 

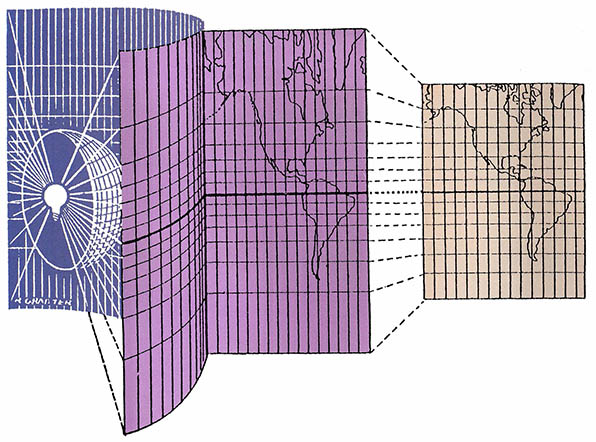
이 도법은 원통도법의 원리를 적용한 것이지만 원통에 투영된 것을 그대로 사용한 것이 아니라 원통에 접하는 적도로부터 극지방으로 갈수록 경선과 경선 사이(동서방향)가 확대되며 이와 같은 비율로 위선 간격을 조정한 것이다(그림 4). 예를 들면 실제로는 위도 60˚의 경선과 경선 간격은 적도의 2분의 1밖에 되지 않지만, 원통도법에 따르면 적도에서나 위도 60˚에서나 같은 간격을 이룬다. 즉 위도 60˚에서는 동서간격이 두배로 확대돼야 하기 때문에 이 위선상에서는 위선 간격(남북 방향)을 같은 비율로 확대한 것이다.

따라서 이 도법의 단점은 금방 드러난다. 적도에서 멀어질수록 거리의 확대 정도가 커져서 위도 60˚에서는 면적이 4배로 확대되고 극지방에서는 무한으로 확대된다. 예를 들면 극지방에 있는 그린란드섬의 면적은 적도지방에 있는 보르네오섬의 3배가 채 되지 않지만 메르카토르도법에서는 비교가 안될 만큼 그린란드 섬이 커보인다.

위선 간격을 조절해 정각도법이 되도록 한 것과 같은 원리로 위선 간격을 적도로부터 멀어질수록 실제보다 좁게 해 면적의 확대되지 않도록 하는 것도 가능하다. 그러나 이 경우는 정각도법의 특성을 잃게 되며 모양도 고위도로 갈수록 크게 일그러져 메르카토르도법과 전혀 다른, 원통도법에 의한 정적도법이 되고 만다.
 

메르카토르도법은 원통 속에 지구의의 적도가 접하도록 놓고 투영한 것이기 때문에 적도 대신 특정 경선이 원통에 접하도록 지구의를 돌려 놓을 수 있다. 이같은 도법을 횡축 메르카토르도법이라 한다. 이때 원통과 접하는 이 특정 경선을 따라 남북으로 길게 놓여있는 지역은 거리나 면적의 확대가 적어 정각의 특성을 지니면서도 면적이 비교적 정확하고 모양의 일그러짐도 적다(그림 5). 이런 장점 때문에 남북으로 길게 놓여있는 우리나라는 횡축 메르카토르 도법의 원리에 의해 1 대 5만, 또는 1대 2만5천과 같은 축척의 지형도를 제작하고 있다.

세계지도를 만들 때는 메르카토르 도법에서 극지방이 무한대로 확대되는 것과 같이 횡축 메르카토르도법에서는 원통과 접하는 경선, 즉 중앙경선으로부터 멀어질수록 거리 확대가 커진다.

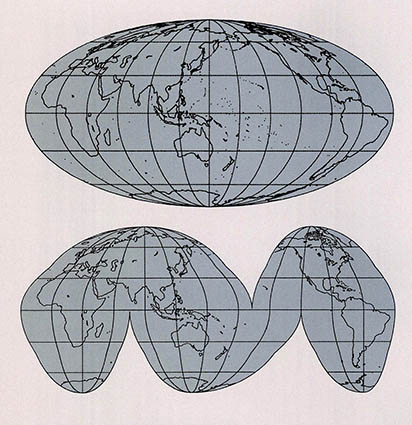
여러 나라의 크기를 비교하거나 섬이나 호수, 기타 지리적 사실을 세계지도나 대륙지도에서 비교할 때는 면적이 비교적 바르게 나타나는 도법에 의한 지도를 사용해야 한다. 앞에서는 면적과 모양이 바르게 나타나는 지도가 있을 수 없음을 살펴보았는데, 모양이 크게 일그러지는 것을 감수한다면 면적이 바르게 나타나는 지도가 불가능한 것은 아니다. 도법에 따라서는 바다부분을 분리시킴으로써 대륙의 모양이 일그러지는 것을 줄일 수도 있다(그림 6).
 

사용 목적에 따라 지도 선택해야

지구의에서의 거리가 지도에 그대로 표현되지 못하는 것과 마찬가지로 지구의의 임의의 한 점에서 모든 방향에 이르는 직선은 지도에서 직선으로 나타나지 않는다. 지구의에서 두 지점간을 직선으로 이을 때 두 지점을 연결하는 최단 거리가 되며 이를 방향이라고 한다.

두 지점이 모두 동일한 경선에 놓여 남북 방향을 이루거나 또는 동일한 위선상에 놓여 동서 방향을 이루는 경우를 제외하고 모든 최단거리를 표시하는 방향은 경선을 통과할 때마다 경선과 이루는 각도가 각각 다르다.

서울과 미국 로스엔젤레스간의 최단 거리와 방향을 살펴보자. 이들 두 지점을 잇는 직선이 최단 거리가 되기 위해서는 어떻게 해야 할까. 지구의에 있는 두 지점과 지구의의 중심을 연결하는 하나의 평면을 가정할 때 이 평면은 지구의를 정확히 같은 크기로 자른다. 이때 이 평면이 지구의의 표면에 표시되는 부분이 최단 거리가 되는 것이다.

이와 같이 지표상에서 지구의에서 두 지점간의 최단 거리는 단 하나 밖에 없고, 이 선을 연장하면 지구의를 두 개의 반구로 나눈다. 이러한 두 지점간의 최단 거리를 이루는 선을 대권(great circle)이라고 하며 이 대권을 이루는 선이 바로 정확한 방향이 되는 것이다. 즉 두 지점간의 대권, 최단거리, 방향은 모두 같은 의미를 지닌 것이다.

서울과 로스엔젤레스 사이의 대권을 지구의에 표시해보면 이 대권이 알래스카를 통과함을 알 수 있다. 실제로 우리나라의 비행기가 서울에서부터 미국 뉴욕이나 로스엔젤레스로 운항하는 직행항로가 알래스카를 통과하는 이유는 이것이 최단거리이기 때문이다(그림 7).

메르카토르 도법에 의한 세계지도에서 서울과 로스엔젤레스를 직선으로 연결하면 이 선은 항상 각 경선을 같은 각도로 통과한다. 예를 들어 이 선이 북쪽에서부터 동쪽으로 95˚ 기울어져 있다고 하면 이를 N 95˚E라고 표시하고 방위각이 N 95˚E라고 부른다. 이 경우 출발지에서부터 같은 각도를 유지해 계속 진행하면 목적지에 닿는다.

경선에 대해서 같은 각도를 이루는 선을 항정선(航程線, rhumb line)이라고 하는데, 이 항정선은 최단 거리나 대권을 표시하지 않을 뿐만 아니라 정확한 방향을 표시하지도 않는다. 다만 정각 도법으로 만들어진 지도는 이 선이 직선으로 표시되도록 했기 때문에 최단 거리처럼 보일 뿐이다. 결국 대권과 항정선을 동시에 직선으로 표시할 수 있는 지도가 있을 수 없기 때문에 사용하는 목적에 따라 지도를 선택해야 하는 것이다.

어떤 도법으로 제작된 세계지도가 가장 좋은 것인가? 이러한 질문에 대한 답은 '그런 지도는 없다'라고 할 수밖에 없다. 지도의 4가지 특성을 그대로 보여주는 것은 지구의 밖에 없기 때문이다.