d라이브러리

우리가 살고 있는 지구의 나이는 얼마나 될까? 이런 의문은 지구상에 인류가 태어나면서부터 제기돼 온 문제일 것이다. 그러나 아직도 정확한 답을 우리는 찾지 못하고 있다.

아메리카 원주민의 전설중에 지구의 역사와 관련된 것이 있다.

1519년 스페인이 멕시코 원주민 아즈텍(Aztec)족이 세운 아즈테카 왕국에 쳐들어 갔을 때 지름이 18m나 되고 무게 18메가톤의 돌로 된 원판을 발견했는데, 이 돌은 섬세하게 조각된 캘린더로서 우주의 구조와 지구의 역사에 관한 지식을 나타낸 것이었다. 이 캘린더를 해석한 전설의 내용은 다음과 같다.

지구의 역사에 대한 근세의 해석

아즈텍과 마야 문명이 가지고 있던 이 전설은 4개의 태양에 관한 것인데, 지금의 태양이 있기 전 4시대의 역사가 있었다는 것이다. 이들 각 시대는 모두 큰 변혁으로 끝을 맺었는데, 4시대는 캘린더의 중앙에 사각형으로 표시돼 있다.

첫번째 시대는 지구가 호랑이의 밥이 돼 종말을 맞았고 두번째 시대는 인류가 무서운 바람에 의해 멸망했으며 살아 남은 사람은 바람에 날려가지 않으려고 나무에 매달린 원숭이로 변했다. 세번째 시대에는 사람들이 무서운 돌과 용암의 세례로 멸망했으며 일부는 이를 피하기 위해 새로 변했다. 네번째 시대에는 큰 홍수로 멸망했는데 이때 사람은 물고기로 변했다. 우리가 살고 있는 다섯번째 시대는 앞으로 지진으로 파괴될 것이라고 한다.

지구의 역사에 대한 고대 전설은 허무맹랑한 것으로 생각되나 불과 수세기 전까지만 해도 지구의 역사에 관한 인간의 지식은 보잘 것 없었다.

예로 현대적인 과학문명이 발달한 유럽쪽에서도 AD 1000년 경 페르시아의 조로아스터(Zoroaster)는 지구가 1만2천년 전에 생성됐으며 앞으로 3천년 밖에는 존재할 수 없다고 했다. 또 아일랜드의 주교인 어셔(Ussher)는 히브리 성서를 연구한 끝에 우주의 창조는 BC 4004년 10월 26일 오전 9시에 이루어 졌다고 했으며 그들의 이러한 생각은 한때 광범위하게 인정되고 있었다. 불과 1백년 전까지만 해도 지구의 역사는 수천만년을 넘지 못했다.

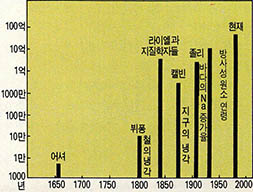
지구의 역사에 대한 사람의 인식을 바꾼 사람들은 지질학자들이다. 18세기 영국의 지질학자 허튼(Hutton)은 지질학적인 연구로 지구의 역사는 이보다 훨씬 길 것으로 생각했다. 1862년 영국의 캘빈은 지구가 잃은 열량을 계산해 지구의 나이는 2천만년에서 4억년 미만으로 생각했다. 또 일부 지질학자들은 시생대 초부터 현세에 이르기까지 퇴적층의 두께가 총 1백60km로 측정됐으므로 연 평균 1mm씩 퇴적되는 것으로 해 1억 6천년으로 생각하기도 했다.

지구의 나이는 바다 속의 염분을 이용해 추정하기도 했다. 바다 속에 들어 있는 나트륨의 총량을 1년동안 육지에서 바다로 운반되어 들어가는 양으로 나누어 추정했다. 즉 바다 속 나트륨의 양은 16×${10}^{15}$g이며 1년에 바다로 운반되는 나트륨의 양은 16×${10}^{7}$g이므로 지구의 연령을 1억년으로 추정했다. 지금 우리가 알고 있는 46억년과는 너무 거리가 먼 값이다(그림 1).
 

방사성 원소 발견 후 지구나이 측정가능
 

지구의 역사를 알게 한 것은 방사성 원소를 이용한 측정법이다. 지사 연구법칙을 이용한 상대적인 연대를 나타내기는 했으나 정량적인 연대학, 즉 절대 연대로 나타내게 된 것은 방사성 원소가 발견된 19세기 말 이후에야 가능하게 됐다.

그것은 X선을 발견한 뢴트겐, 우라늄의 방사능을 발견한 베크렐, 그리고 우라늄에 섞여 있는 라듐을 분리한 퀴리부부 등 학자들의 연구 결과로 우라늄 라듐과 같은 원자량이 큰 원소가 방사선을 내면서 일련의 변화과정을 거쳐 납으로 바뀐다는 것을 알아내고 이들 방사선의 정체가 구체적으로 밝혀지면서 보다 과학적인 지구의 나이추정이 가능하게 됐다.

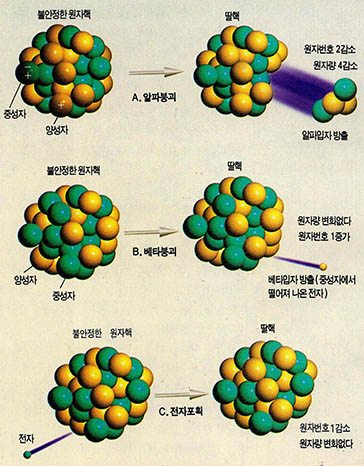
원자는 원자핵과 원자핵 주위를 빠른 속도로 도는 전자로 구성돼 있다. 또 원자핵은 양성자 중성자 중간자 등으로 구성돼 있다. 자연상태에서 많은 수의 원자핵들은 불안정하다. 즉 에너지 관점에서 볼 때 원자핵 부분들의 결합에너지의 합이 처음 원자핵의 결합에너지보다 크기 때문에 불안정한 원자핵들은 둘 또는 그 이상의 부분으로 분리될 수 있다. 원자핵은 여러가지 불안정한 방법으로 분리될 수 있으나 일반적으로 방사성 붕괴라는 말은 알파(α) 베타(β) 감마(γ) 복사와 함께 다른 원자핵으로 변하는 붕괴(그림 2)를 말한다.

여기서 알파 붕괴란 러더포드에 의해 ${ }^{4}$He핵의 방출임이 확인됐으며 베타 붕괴는 양 또는 음으로 하전된 전자임이 판명됐고, 또한 감마선은 전자기 복사임이 밝혀졌다.
 

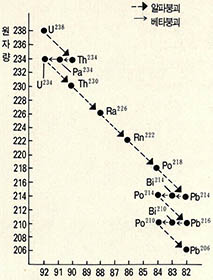
가장 잘 알려진 우라늄의 붕괴(그림 3)를 살펴보자. 우라늄은 그림과 같은 복잡한 과정을 거쳐 납으로 붕괴한다. 민약 1g의 우라늄이 모두 납으로 되는 데 걸리는 시간은 얼마일까? 우라늄이 붕괴해 1/2g이 되는 데에는 약 45억년이 걸린다. 그 나머지 1/2g이 다시 1/2로 되는 데에도 역시 45억년이 걸린다. 이때 45억년을 우라늄의 반감기라고 한다. 방사성 원소는 이처럼 반감기라는 이상한 나이를 먹는다.

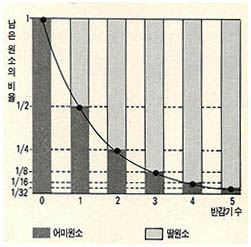
우라늄이 붕괴해 감소되는 양을(그림 4)로 나타냈는데, 이때 우라늄을 어미원소, 그 생성 물인 납을 딸 원소라 한다.

반감기는 방사성 원소가 붕괴해 처음 양의 절반이 되는 데까지 걸린 시간을 말한다. 그러면 1/2, 1/4 … 극미량의 우라늄이 남아도 역시 남은 양의 절반으로 되는 데에는 45억년이 걸린다. 그러면 우라늄의 마지막 원자 2개가 남았을 경우에도 1개가 붕괴해 1개 원자가 남는 데에도 45억년이 걸릴까? 그러나 방사성 원소의 반감기는 원소에 따른 붕괴확률로 계산된 것이므로 이처럼 통계적인 방법이 적용되기 어려운 경우에는 단언하기 어렵다. 즉 45억년이 지나도 이들은 붕괴하지 않을 수도, 그보다 훨씬 짧은 시간이 경과한 후에 붕괴할 수도 있는 것이다.

(표)는 여러 원소의 반감기를 나타낸 것이다.
 

방사성 원소의 붕괴시간

방사성 원소의 붕괴 법칙을 이해하기 위해 여기 두 개의 상자에 주사위 2백개와 1백개가 각각 들어 있다고 하자. 주사위의 한 면에 *를 표시해 일정한 시간 흔든 후 *가 위로 향한 것을 붕괴한 것으로 가정하자. 단위 시간당 어느 것이 더 많이 붕괴하겠는가? 여기서 단위 시간당 붕괴수를 붕괴율(R)이라고 하면 물론 많은 양의 주사위가 들어 있는 상자에서 붕괴율이 클 것이다. 방사성 원소의 붕괴율은 이처럼 초기의 방사성 원소의 수(N)에 비례한다.

한편 이번에는 보통 6면체로 돼 있는 주사위와 8면체로 돼 있는 주사위가 두 상자에 1백개씩 들어 있다고 하자. 마찬가지로 각 주사위의 한면에 *를 하여 일정한 시간 상자를 흔들고 *면이 위로 향한 것을 붕괴한 것으로 가정한다면 붕괴율(R)은 어떻게 될까? *가 나올 확률이 6면체는1/6, 8면체 주사위는 1/8이므로 6면체 주사위가 든 상자에서 더 많은 붕괴가 일어날 것이다. 이처럼 방시성 원소의 붕괴율은 방사성 원소에 따라서도 다른데, 이를 붕괴상수(λ)라고 한다.

여기서 주사위가 마지막 두개 남았다고 하자. 이들이 모두 붕괴하는 데에는 시간이 얼마나 걸릴까? 어떤 사람은 동시에 두 개가 붕괴하고, 어떤 경우는 하루 종일 흔들어도 붕괴하지 않을 수도 있을 것이다. 붕괴율, 붕괴상수는 이처럼 통계적인 수치다.

방사성 원소의 붕괴 법칙

방사성 원소의 시료 가운데 N을 어떤 시각에서 방사성원소의 원자핵의 수라면 dt시간에는 dN만큼 감소될 것이다. 따라서 붕괴율 R은

R=-$\frac{dN}{dt}$이며 방사성 원소에 따라 붕괴하는 확률이 다를 것이므로, 어떤 방사성 원소의 붕괴 상수를 λ라 하면

R=-$\frac{dN}{dt}$=λN이고, 또한 방사성 원소가 ${N}_{0}$개일 때의 붕괴율을 ${R}_{0}$라 하면 ${R}_{0}$=$\frac{d{N}_{0}}{dt}$=λ${N}_{0}$가 된다. 여기서 ${N}_{0}$를 ${t}_{0}$, N을 t때의 원자핵수라고 할 때, 이를 적분하면

${{∫}^{N}}_{{N}_{0}}$$\frac{dN}{n}$=ℓ${{∫}^{t}}_{to}$dt=λ(t-to)
ℓn$\frac{N}{{N}_{0}}$=-λ(t-to) $\frac{N}{{N}_{o}}$=${e}^{-λ(t-to)}$ 의 관계가 성립한다.

한편 원자핵의 개수와 붕괴율 R은 비례하므로
$\frac{R}{{R}_{o}}$=${e}^{-λ(t-to)}$ 가 된다.

어떤 방사성 원소의 반감기를 T라면 반감기는 원자핵의 수가 처음의 1/2로 되는 데 걸린 시간이므로 t-${t}_{0}$=T이며 $\frac{N}{{N}_{0}}$=$₩frac{1}{2}$ 이므로 $\frac{N}{{N}_{0}}$=${e}^{-λ.T}$, -λ·T=ℓn$\frac{1}{2}$, λ·T=0.693이 된다.

따라서 어떤 방사성 원소가 수초에서 수일까지의 반감기를 갖는 경우에 여러 시간대에서 붕괴율 R을 측정하고 측정된 R에서 λ를 구할 수 있으므로 반감기 T를 알 수 있다.

예를 들어 처음에 1초당 5백번의 붕괴수가 있는 방사성 원소가 한 시간 후에는 1초당 4백번으로 줄어 들었다고 할 때 이 물질의 반감기를 위 식에서 구해보면

$\frac{R}{{R}_{o}}$=${e}^{-λ(t-to)}$ 에서
λ=$\frac{1}{t-to}$ℓn$\frac{{R}_{o}}{R}$=$\frac{1}{1.0}$ℓn$\frac{500}{400}$=0.223
T=$\frac{ℓn2}{λ}$=$\frac{0.693}{0.223}$=3.1(hr)가 된다.

한편 반감기가 아주 긴 ${ }^{238}$U의 경우에는 근사적으로 구할 수 밖에 없다.

정체 불명의 상수 7.5×${10}^{9}$

우라늄을 이용한 암석의 연대 측정에는 보통 우라늄 과 생성된 납의 비를 측정해 7.5×${10}^{9}$을 곱해 정하는 것으로 배우고 있다.

Age=$\frac{{M}_{Pb}}{Mu}$×7.5×${10}^{9}$

여기서 7.5×${10}^{9}$은 어디서 나온 것인가?

${ }^{238}$U가 t시간 동안 붕괴해 ${ }^{206}$Pb가 될 때 Nu'를 초기 우라늄의 원자핵수라면 dt시간 동안 붕괴하고 남은 우라늄의 원자핵수는 Nu'·${e}^{-λt}$이므로 생성된 납원자핵수${N}^{Pb}$는 ${N}^{Pb}$=Nu'-Nu'·${e}^{-λt}$=Nu'(1-${e}^{-λt}$) 한편 $\frac{Nu}{Nu'}$=${e}^{-λt}$이므로 ${N}^{Pb}$=Nu(${e}^{λt}$-1) 여기서 λt≪1이면 테일러 급수 정리에서 ${e}^{λt}$=1+λt이므로 ${N}^{Pb}$=Nu'·λt가 된다.

그러므로 우라늄과 납의 원자핵의 수의 비를 측정하면 경과한 시간 Age는 Age=$\frac{{M}_{Pb}}{Mu}$·$₩frac{1}{λ}$

반감기를 T라 하면 우라늄의 반감기는 45억년이므로 λ=$\frac{0.693}{T}$에서
Age=$\frac{{M}_{Pb}}{Mu}$×45억년×$\frac{1}{0.693}$=$\frac{{M}_{Pb}}{Mu}$×6.5×${10}^{9}$

그런데 두 원소의 원자량이 각각 238,206이므로 질량비로는
Age=$\frac{{M}_{Pb}}{Mu}$×$\frac{238}{206}$×6.5×${10}^{9}$=$\frac{{M}_{Pb}}{Mu}$×7.5×${10}^{9}$가 된다.

암석의 절대연령 측정
 

암석의 연령은 방사성 원소를 추출, 반감기를 이용해 절대 연령을 측정하는데, 그 방법에는 다음과 같은 여러 가지가 있다.

·U-Pb예법 : 우라늄을 포함한 광물을 분석해 그 중에 들어 있는 우라늄에 대한 납의 양의 비를 측정해 그
광물의 생성 시대를 알아낸다. 그런데 우라늄은 질량번호가 238인 것 이외에 235인 것이 1/140 정도 들어 있다. ${ }^{235}$U는 원자탄의 제조에 쓰이는 우라늄의 동위원소로 7개의 α입자를 방출하고 ${ }^{207}$Pb로 변한다. 또한 우라늄과 종종 같이 들어 있는 ${ }^{232}$Th도 6개의 α입자를 방출하고 ${ }^{208}$Pb로 붕괴하며, 자연계에는 보통의 납인 ${ }^{204}$Pb도 있으므로 이들을 구별하지 않고 그대로 측정한다면 납의 양이 과다하게 측정돼 실제보다 오랜 것으로 측정된다. 그러나 다행히 질량 분광기를 발명, 질량 번호별로 납의 질량을 측정할 수 있게 돼 연대 측정이 가능해졌다.

이 방법은 ${ }^{238}$U-${ }^{206}$Pb과 ${ }^{235}$U-${ }^{207}$Pb의 두 가지 방법으로 동시에 측정할 수 있으므로 두가지 방법에 의한 측정치가 일치되면 그 암석의 연령은 거의 정확한 것으로 여길 수 있다.

·K-Ar법 : 방사성 원소 ${ }^{40}$K는 ${ }^{40}$Ar으로 붕괴, 밖으로 방출돼 버리나 마그마가 식어서 암석으로 굳은 다음에 생성된 ${ }^{40}$Ar은 화성암 내에 축적되므로 ${ }^{40}$K의 양과 축적된 ${ }^{40}$Ar의 양을 측정하면 화성암이 연령을 측정할 수 있다. 이 방법으로는 화성암이 분출해 굳어진 후 10만년 이상된 암석의 연령 측정이 가능해 ${ }^{14}$C방법으로 측정되는 최대 연수와 연결이 가능하게 됐다.

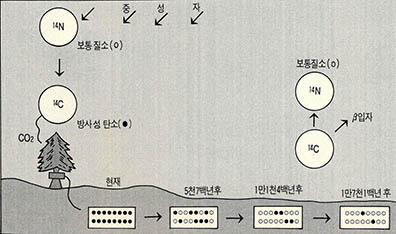
·방사성 탄소법 : 1946년 리비(Ribby)에 의해 개발된 방법이다. ${ }^{14}$N는 우주선중의 중성자에 의해 ${ }^{14}$C로 변하는 데 ${ }^{14}$C는 불안정해 전자를 방출하고 다시 ${ }^{14}$N가 된다(그림 5).

그런데 살아 있는 식물체는 공기증의 ${CO}_{2}$를 흡수해 탄소동화작용을 한다. 그러므로 식물체를 이루는 탄소화합물 중의 방사성 탄소와 일반 탄소의 비가 공기중에 포함된 두 원소의 비와 같으나 생물체가 죽으면 시간이 지남에 따라 방사성 탄소의 양은 감소되므로 죽은 식물체 안의 ${ }^{14}$C의 양을 측정해 연대를 측정할 수 있다. 측정 가능한 연수는 4만년 정도다.

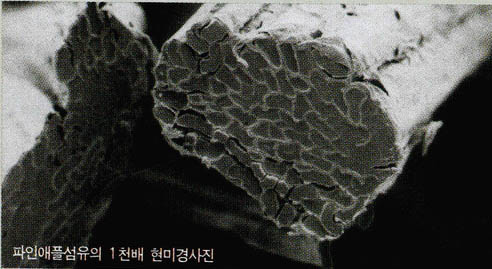
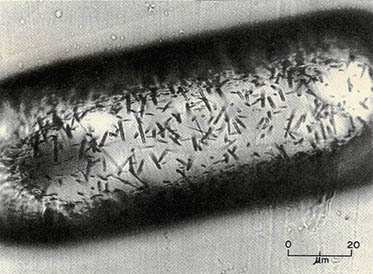
·분열 비적법 : 지르콘과 같은 광물 속에 들어있는 우라늄이 붕괴하면 α입자를 방출한다. 방출된 α입자는 광물 속을 지나면서 통과한 자리에 (사진)과 같은 비적(飛跡)을 남긴다.

이 비적은 너무나 가늘기 때문에 산이나 알칼리용액으로 처리해 비적을 넓혀 단위면적당의 수를 센다. 한편 이 표품(標品)에 들어 있는 우라늄의 양을 알기 위해 반응로에 넣어 중성자로 때려서 광물 속의 우라늄을 전부 분열하게 하고 이때 방출된 α입자에 의해 형성된 비적을 센다. 이를 비교하면 지금까지 붕괴한 우라늄과 광물 속에 포함된 우라늄 총량의 비를 알 수 있으므로 수백년의 연령에서 수십억년까지의 연령측정이 가능하다. 이 분열비적법은 또한 화산재가 굳어진 응회암의 연령 측정도 가능하다. 최근 아프리카에서 응회암층에 남겨진 인류의 발자국 화석도 이 방법으로 연대를 측정해 3백만년 전의 것임을 밝힐 수 있었다.