축구공은 5각형과 6각형 무늬로 구성돼 있는데 일일이 세보지 않고도 총 무늬수를 알 수 있다.
풀어보고
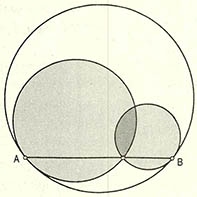
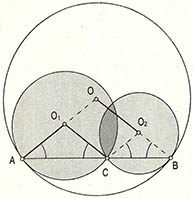
(1) 한 원 안에서 두개의 원이 서로 만나고 있다. 그 하나는 큰 원과 A에서, 다른 하나는 B에서 접하고 있다. 만약 (그림)과 같이 선분 AB가 이 두 작은 원과 한 공통점에서 만난다면, 큰 원의 반지름 R과 작은 원의 반지름 ${r}_{1}$, ${r}_{2}$의 관계는 무엇일까? 여러가지 방법으로 시도해 볼 수 있지만 가장 쉽게 관계를 밝혀낼 수 있는 보조그림을 찾는 것도 중요하다.
① R=${r}_{1}$+${r}_{2}$ ② R=2(${r}_{1}$+${r}_{2}$) ③ R>${r}_{1}$+${r}_{2}$ ④ R>2(${r}_{1}$+${r}_{2}$)
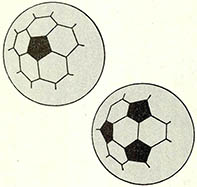
(2) 시중에 나와 있는 축구공을 잘 보면, 한 가지의 무늬로 돼 있는 것이 아니라 (그림)처럼 5각형과 6각형의 무늬로 구성돼 있다. 5각형의 입장에서 보면 주위에 5개의 6각형이 에워싸고 있고, 6각형의 주위로는 3개의 5각형과 6개의 6각형이 번갈아 에워싸고 있다. 5각형의 개수가 세어보니 12개다. 6각형의 개수를 구하라.
① 10 ② 12 ③ 18 ④ 20
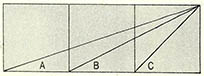
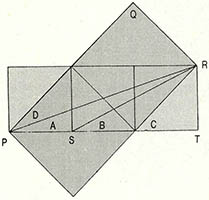
(3) (그림)과 같이 정사각형 세개가 연결돼 있다. 이때 각 C와 각 A, B의 관계는 어떨까? 여러분이 싫어하는(?) 삼각함수를 도입하지 말고 보조그림을 잘 그려서 쉽게 유도해 보라.
① C=A+B ② C=2A+B ③ C=A+2B ④ C=2A+2B
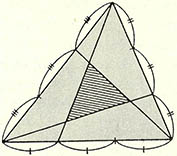
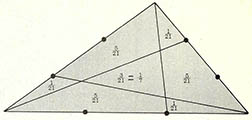
(4) 임의의 삼각형에서, 세 꼭지점에서 맞변의 3등분되는 점으로 직선을 그어 (그림)과 같이 또 하나의 작은 삼각형을 만든다. 이 빗금친 내부의 삼각형 면적은 원래 삼각형 면적의 몇분의 1인가?
① 1/2 ② 1/3 ③ 1/5 ④ 1/7
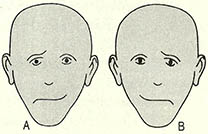
(5) 다음 문제는 수학이라기보다는 심리학 문제로 취급할 수 있다. 그러나 대칭 비대칭성을 이야기할 때 빈번히 등장하는 테스트이기도 하다. 다음 (그림)에서 어느 쪽 얼굴이 더 행복하게 보이는가?
① A>B ② B>A ③ A=B ④ 무관하다
맞춰보고
(1) ① 큰 원과 두 작은 원의 중심과 반지름을 각각 0, ${0}_{1}$, ${0}_{2}$, R, ${r}_{1}$, ${r}_{2}$라 하자. 선분 AB가 두 작은 원과 C에서 만난다고 하면 삼각형 OAB와 ${0}_{1}$AC, ${0}_{2}$CB는 각각 이등변삼각형이고 각 ${0}_{1}$AC와 각 ${0}_{2}$BC가 같으므로 셋이 서로 닮은꼴이다. 따라서 0${0}_{1}$C${0}_{2}$는 평행사변형이 되어 0${0}_{2}$=${0}_{1}$C=${0}_{1}$A가 되고, R=OB=O${0}_{2}$+${0}_{2}$B=${0}_{1}$C+${0}_{2}$B=${r}_{1}$+${r}_{2}$가 돼, 큰 원의 반지름은 작은 원의 반지름의 합이다.
(2) ④ 5각형 주위에는 5개의 6각형이 에워싸고 있으므로, 각각의 5각형에 대해 6각형을 세어봤다면 5각형이 12개이므로 6각형은 60번 헤아려지게 된다. 그런데 이 숫자는 6각형이 중복돼서 헤아려진 결과가 된다. 다시 말해 5각형 주위의 6각형에 셀 때마다 표시를 하면 6각형에는 표시가 중복될 것이다. 몇 번 중복됐을까?
6각형에는 3개의 5각형, 3개의 6각형이 에워싸고 있으므로, 결국 6각형은 3개의 5각형으로부터 각각 세어지게 돼, 위 숫자(60)는 3번 중복된 숫자가 된다. 시판되고 있는 축구공의 무늬를 세어보면 20개의 6각형을 확인할 수 있을 것이다. 이것은 레크리에이션수학이 야구 등의 통계 뿐만 아니라 스포츠와 많은 관련이 있음을 보여주는 예다.
(3) ① 이 문제에 대한 증명으로는 그동안 많은 해답이 나와 있다. 1971년에는 54개의 다른 방법이 발표됐고, 종이 자르기로 증명한 방법도 있을 뿐만 아니라 3개 이상인 n개의 정사각형이 연속돼 있을 때의 증명도 나와 있다. 삼각함수를 안 쓰고 보조 그림을 통해 쉽게 알 수 있는 증명으로 다음 (그림)을 보자.
보조그림으로 정사각형의 대각선을 연장, 두 개의 다른 정사각형을 연결했다. 이때 각 B와 각 D는 같다. 왜냐하면 두 각이 다 길이가 2:1인 직각삼각형 PQR, RST의 각이기 때문이다. (그림)에서 각 C=각 A+각 D=각 A+각 B임을 쉽게 알아 볼 수 있다.
(4) ④ 이렇게 각 꼭지점에서 맞변의 임의의 점에 내린 선분을 17세기 이탈리아의 수학자 지오바니 세바(Giovanni Ceva)의 이름을 따 세비안(Cevian)이라고 부른다. 문제에서와 같이 3등분하는 점에 선을 그어 작도하면 (그림1)과 같이 1/21, 3/21, 5/21의 크기를 갖는 7개의 부분으로 나눠진다. 즉 내부의 삼각형 크기는 3/21=1/7이 된다.
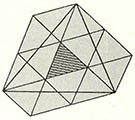
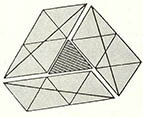
이 문제는 역사가 길어서 재치있는 증명들이 많이 있지만, 다음 그림에서 보면 쉽게 알 수 있다. 내부의 삼각형과 평행한 선들을 그어 (그림2)처럼 육각형을 만든다. 이 육각형 속에는 작은 삼각형이 13개 있게 된다. 원래의 삼각형을 잘 보면 (그림3)에서 보듯이 4개짜리 평행사변형의 반에 해당되는 부분이 3개 있어 이들의 합 6개와 내부의 작은 삼각형을 합해 모두 7개의 작은 삼각형이 있는 셈이다. 즉 빗금친 내부의 작은 삼각형은 원래 삼각형의 1/7이다.
(5) ② (오른손잡이의 관점에서). 이 세상이 대칭인가 아닌가 하는 문제는 당장 우리의 얼굴이 대칭인가 하는 것으로부터 시작해서, 공학적으로 대칭이면 문제풀기가 훨씬 쉬워진다는 것 뿐만 아니라, 우주의 비밀을 알아내는데 매우 중요한 의미를 갖고 있다. 유명한 가드너(M. Gardner)는 1990년에 펴낸 책(The New Ambidextrous Universe)에서 이 문제에 대해 폭넓게 잘 정리해 놓고 있다.
좀 더 편한 마음으로 대할 수 있는 이 문제를 보자. 독자들은 어떻게 느꼈을까? 이 문제의 얼굴들은 좌우대칭이지만 일반적으로 오른손잡이에게는 B가 더 행복한 얼굴이라고 느껴지고 왼손잡이에게는 그 반대라는 것이다. 왜 그럴까? 정확한 답은 1977년에 출간된, 이 문제의 출처인 줄리안 제인스(Julian Jaynes)의 책(The Origin of Consciousness in the Breakdown of the Bicameral Mind)에 넘기고, 이런 문제들로부터 인간과 우주의 비밀에 대한 도전이 시작된다는 것만을 전하고 싶을 뿐이다.