d라이브러리

좌우대칭을 이루면 보기에도 아름답다. 우리 주변에는 절묘한 대칭성을 나타내는 숫자들이 많이 있다.

풀어보고

(1) 1 ,2, 3, 4, 5, 6, 7, 8, 9를 작은 순서대로 늘어놓고 4칙부호(＋, －, ×, ÷)를 넣어서 100을 만들고 싶다. 다음 중 틀린 것은?

① 1＋2＋3＋4＋5＋6＋7＋(8×9)＝100
② 123－4－5－6－7－8－9＝100
③ 123＋45－67＋8－9＝100
④ 123－45－67＋89＝100

(2) 1에서 9까지의 숫자중 8이 빠진 12345679는 특별한 숫자이다. 12345679×51의 값은?

① 419419419 ② 516516516 ③ 629629629 ④ 815815815

(3) 수는 대칭성 등을 통하여 아름다움을 발견할 수 있다. 다음의 수식모음중 틀린것은?

①     1 x 95 = 19 x 5
      1 x 995 = 199 x 5
    1 x 9995 = 1999 x 5
  1 x 99995 = 19999 x 5
1 x 999995 = 199999 x 5

②     4 x 98 = 49 x 8
      4 x 998 = 499 x 8
    4 x 9998 = 4999 x 8
  4 x 99998 = 49999 x 8
4 x 9999998 = 499999 x 8

③    6 x 545 = 654 x 5
     6 x 54545 = 65454 x 5            
   6 x 5454545 = 6545454 x 5        
 6 x 545454545 = 654545454 x 5    
6 x 54545454545 = 65454545454 x 5

④    323 = 17 x19
     33233 = 177 x 199
   3332333 = 1777 x 1999
  333323333 = 17777 x 19999
33333233333 = 177777 x 199999

(4) 가, 나, 다, 라 네사람의 체중을 두 사람씩 한조로 측정하였더니 다음과 같은 결과를 얻었다. 108, 115, 119, 121, 125, 132(단위 ㎏). 이 네사람의 체중은 각각 얼마일까?

① 36, 41, 52, 60 ② 40, 49, 51, 59 ③ 51, 57, 64, 68 ④ 53, 59, 63, 71

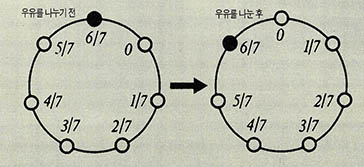
(5) 일곱난쟁이가 백설공주를 기다리며 테이블 주위에 둥그렇게 앉았다. 이 일곱난쟁이들은 모두 우유를 담은 커다란 컵을 들고 있었다. 첫번째 난쟁이가 자기 컵 속에 든 우유를 6등분하여 다른 난쟁이들의 컵 속에 부어넣었다. 그 다음 난쟁이도 똑 같이 하고, 그 다음도, 그 다음도 모두 따라서 했다. 일곱번째 난쟁이가 다 따르고 나니 각 난쟁이가 갖고 있는 컵 속에 남은 우유가 시작할 때와 똑같았다. 전체의 우유량이 3ℓ라면, 각 난쟁이의 컵에는 원래 얼마만큼씩의 우유가 있었을까? 제일 많은 컵에 얼마의 우유가 있었는가로 답해 보시오.

① $\frac{2}{3}$ ② $\frac{6}{7}$ ③ 1$\frac{1}{2}$ ④ 1$\frac{3}{4}$
 

맞춰보고

(1) ②두번째 식을 맞는 식으로 고치면 다음과 같다.
123－4－5－6－7＋8－9＝100
이 외에도 다음과 같은 식들이 가능하다.
1＋2＋34－5＋67－8＋9＝100
12＋34－5＋67＋8＋9＝100
123＋4－5＋67－89＝100
이 숫자를 반대로 배치하면 다음과 같은 식을 얻을 수 있다.
98－76＋54＋3＋21＝100

(2) ③12315679 × 51 ＝ 629629629이다. 올해로 국민의 승리인 6.29선언의 5주년이 되었다. 이 날짜를 숫자를 써서 기념해 볼 수 있다는 것이 묘미가 있다. 1부터 9에서 8이 빠진 12345679는 재미있는 성질이 있어 여러 숫자놀이에 응용되고 있다.
(i) 12345679 × 9 ＝ 111111111
12345679 × 18 ＝ 222222222
12345679 × 27＝ 333333333
12345679 × 36 ＝ 444444444
12345679 × 45 ＝ 555555555
(ii) 12345679 × 24 ＝ 296296296
12345679 × 51＝ 629629629
12345679 × 78 ＝ 962962962 등이다.
또 12345679 × 51－12345679 × 24 ＝ 629629629－296296296 ＝ 33333333
12345679 × 78－12345679 × 51 ＝ 962962962－629629629 ＝ 333333333 등과 같은 연관식들이 나타난다.

(3) ④ 4번째식은 다음과 같이 되어야 한다.
       323 = 17 x 19
    33233 = 167 x 199
  3332333 = 1667 x 1999
 333323333 = 16667 x 19999
33333233333 = 166667 x 199999

이와같은 숫자의 아름다운 대칭미를 나타내주는 것은 매우 많지만 문제의 예들과 같은 맥락에 있는 것들만 살펴보면 다음과 같다.

      1 x 64 = 16 x 4        
    1 x 664 = 166 x 4      
  1 x 6664 = 1666 x 4    
 1 x 66664 = 16666 x 4  
1 x 666664 = 166666 x 4

    2 x65 = 26 x 5        
   2 x 665 = 266 x 5     
  2 x 6665 = 2666 x 5   
 2 x 66665 = 26666 x 5 
2 x 666665 = 266666 x 5

        7 x 424 = 742 x 4
      7 x 42424 = 74242 x 4
    7 x 4242424 = 7424242 x 4
  7 x 424242424 = 742424242 x 4
7 x 424242424242 = 74242424242 x 4

          4 x 847 = 484 x 7                  
         4 x 84847 = 48484 x 7              
    4x 8484847 = 484848484 x 7         
 4 x 84848484847 = 48484848484 x 7  
4 x 8484848484847 = 48484848484 x 7

           343 = 7x 49
        33433 = 67 x 499
     3334333 = 667 x 4999
   333343333 = 6667 x 49999
333334333333 = 66667 x 499999

(4) ③네사람의 체중을 두사람씩 한조로 하여 측정한 결과가 6개다. 모두 12명의 체중을 쟀고, 결과가 다 다르니 모두 똑같이 참여한 결과다. 따라서 6개 결과의 합은 네사람 체중의 세배가 된다. 즉 (가＋나＋다＋라)＝(108＋115＋119＋121＋125＋132)÷3＝240 또 가나다라 순으로 체중이 커진다고 하자. 그러면 작은 두 체중의 합으로부터

가＋나＝108…①
가＋다＝115…②의 두 식이 명백하다.
또 무거운 두 체중의 합으로부터
다＋라＝132…③
나＋라＝125…④의 두 식이 명백하다.
또 가+다=115…②
 - 가+나=108…①
   다-나=7

즉 다=나+7

따라서 나＋다＝나＋(나＋7)＝2×나＋7.
만일 나＋다＝119라면 나＝56, 다＝63이고, ①에서 가는 44 ②에서 52가 되어 답이 모순된다. 따라서 나＋다＝121이고 나＝57, 다＝64, 가＝51, 라＝68이다.

(5) ②유추법(때려 맞추고 답이 맞나를 확인하는 법)에 의하면 각 난쟁이의 컵에는 0, $\frac{1}{7}$, $\frac{2}{7}$, $\frac{3}{7}$, $\frac{4}{7}$, $\frac{5}{7}$, $\frac{6}{7}$ℓ씩 들어 있었다. 문제 5번의 그림처럼 $\frac{6}{7}$컵을 든 난쟁이가 나누어 붓는 경우를 보면, 그 결과는 똑같은 상태가 한 난쟁이만큼 돌아가 있는 것을 알 수 있을 것이다. 결국 이것을 일곱 번 반복하면 원래 그대로 돌아오게 된다. 이런 유추법에서는 이 해답이 유일한(unique) 해답이라는 사실을 밝히는 것이 다음의 필요한 단계다. 약간의 수학을 사용하면 유일한 답임을 증명할 수 있다.