d라이브러리

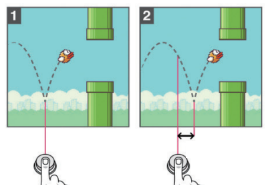
함수로 신경망 따라하기

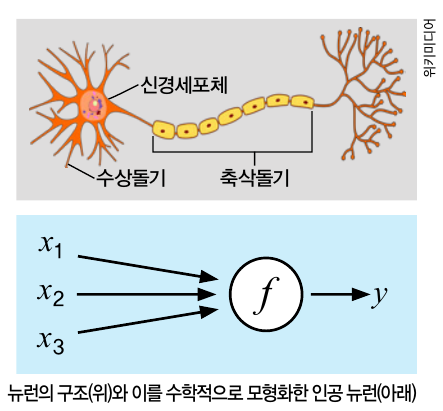
딥러닝에 사용하는 인공신경망은 신경계의 기본 단위인 ‘뉴런’의 작동 원리를 이용해 만들었습니다.  

뉴런의 수상돌기가 화학 신호를 받으면 축삭돌기로 전기 신호가 전달됩니다. 이것이 다시 화학 신호 형태로 축삭돌기 말단에서 다른 뉴런으로 전달되면서 몸에 반응이 일어납니다. 인공 뉴런도 여러 개의 입력 신호 xi를 받아 하나의 신호 y를 출력합니다. 

또 뉴런은 일정 크기 이상의 자극이 주어져야 반응하는데, 이 자극의 크기를 임계값이라고 합니다. 인공 뉴런에서는 각 입력 신호에 고유한 가중치가 부여되는데, 가중치가 클수록 해당 신호가 중요하다는 뜻입니다. 입력 신호(x_i)를 미리 부여한 가중치(w_i)에 따라 계산한 후, 그 총합이 정해놓은 임계값을 넘으면 1을, 넘지 못하면 0을 출력합니다. 이런 함수를 계단함수라고 하고, 다음과 같이 나타냅니다.

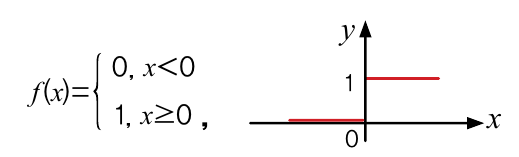
계단 함수처럼 인공 뉴런의 출력을 결정하는 함수를 ‘활성화 함수’라고 합니다. 인공신경망은 활성화 함수를 포함한 여러 개의 인공 뉴런 층으로 구성돼 있습니다.  

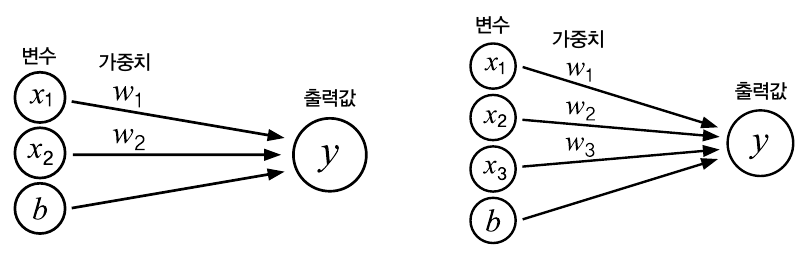
인공신경망의 층을 구성하는 인공 뉴런을 ‘노드’라고 부르는데, 하나의 노드는 입력 신호를 받아 다른 층으로 결과를 전달하는 하나의 함수로 볼 수 있습니다. 입력 신호 x를 받아 y를 출력하는 경우는 y=wx+b로 나타낼 수 있죠. 여기서 w는 가중치, b는 함수가 더 정확한 결과를 내도록 돕는 편향입니다. 입력 신호가 두 개면 y=w₁x₁+w₂x₂+b, 세 개면 y=w₁x₁+w₂x₂+w₃x₃+b와 같이 나타냅니다. 다수의 입력 신호 x₁, x₂,…, x_i가 있는 경우에도 같은 방식으로 표현합니다.

출력값이 두 개인 경우는 행렬의 곱을 이용해 나타냅니다. 이때 wij는 i번째 노드에서 j번째 노드로 연결된 가중치를 의미합니다. 편의상 편향을 0으로 가정하면 다음과 같은 행렬과 그림으로 나타낼 수 있습니다. 

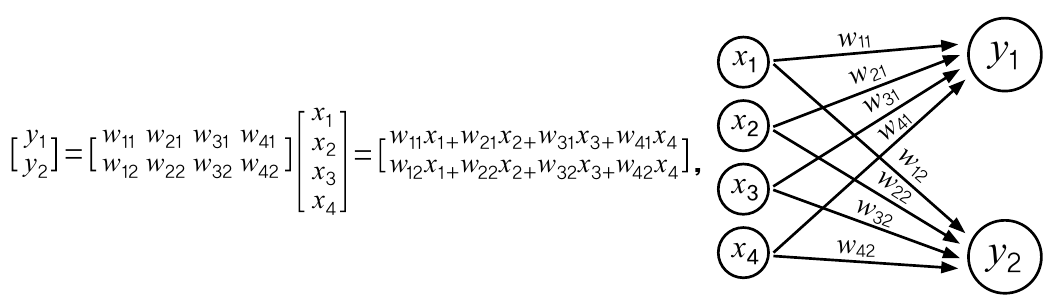
 문제  입력 신호 x에 대한 함수 y=wx+b에서 가중치가 0.5, 편향이 -2일 때의 그래프를 그리고, 여기서 출력된 신호를 앞서 배운 계단함수에 다시 입력했을 때의 결과를 구해보자. 

★  폴리매스 홈페이지→[주니어 폴리매스]→[인공지능, 수학으로 타파]에서 자세한 내용을 확인하세요.