d라이브러리

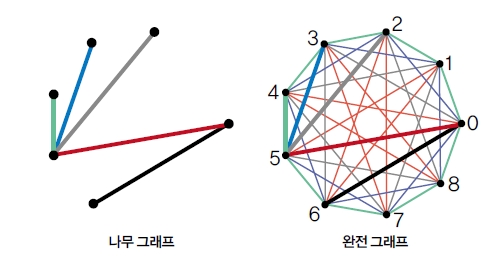
1963년 독일 수학자 게르하르트 링겔은 n+1개의 점을 가진 나무 그래프로 2n+1의 점을 가진 완전 그래프를 완전히 덮을 수 있다는 ‘링겔 추측’을 발표했습니다. 나무 그래프는 점과 점을 연결하는 선으로 이뤄진 순환하지 않는 연결 그래프이고, 완전 그래프는 서로 다른 두 개의 점이 반드시 하나의 선으로 연결된 순환하는 그래프입니다. 

2020년 1월 8일, 3명의 수학자 리처드 몽고메리, 알렉세이 포크로브스키, 베니 수다코프는 링겔 추측의 증명을 온라인 논문 게재 사이트 ‘아카이브’에 발표했습니다. 

완전 그래프에서 한 단위 떨어진 점을 연결하는 모든 선은 같은 색으로, 두 단위 떨어져 있는 점을 연결하는 선은 또 다른 색으로 통일해 색칠해나가면 2n+1개의 점이 있는 완전 그래프의 선을 칠하는 데 필요한 색깔은 항상 n개고, n+1개 꼭짓점을 가진 나무 그래프는 n개의 선을 가지므로 링겔 추측이 성립하는 겁니다. 연구팀은 이를 증명하기 위해 ‘무지개 복사’라는 방법을 이용했습니다. 완전 그래프에서 조건에 맞게 선을 색칠하고 각각의 서로 다른 색을 모두 가진 하나의 나무 그래프를 복사해 전체 그래프를 채우는 방법입니다. 아직 공식적으로 증명이 확인된 상태는 아닙니다. 하지만 논문을 검토한 수학자들은 새로운 발견이라며 흥분하고 있습니다. 질 칼리이 이스라엘 히브리대학교 수학과 교수는 “다른 어떤 방법으로도 풀지 못했던 오랜 추측이 풀려서 기쁘다”고 말했습니다.