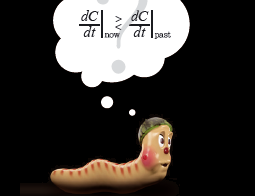d라이브러리

삼각수, 오각수, 육각수라고? 이번에는 숫자와 도형에 대한 질문이로군. 이런 문제는 내가 전문가라고 할 수 있지. ‘오각수 정리’까지 만든 몸이시거든~. 어디 한번 머리 좀 풀어볼까?
 

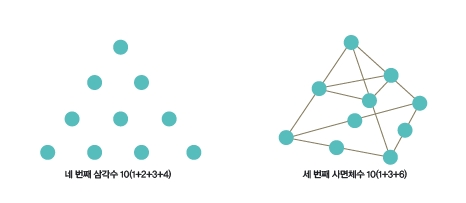
삼각수는 점을 배열해 삼각형을 만들 때 배열된 점의 개수를 말한다. 1을 시작으로 3, 6, 10 등으로 이어지는 수열 형태다. 고대 그리스의 수학자 피타고라스가 만든 단체인 피타고라스학파의 학자들이 삼각수를 연구한 기록을 남겼을 정도로 오래 전부터 수학자들의 관심을 받았다. 특히 피타고라스학파는 네 번째 삼각수인 10을 나타내는 삼각형 무늬를 ‘테트락티스’라 이름붙이고 매우 특별한 상징으로 여겼다.

수학자들은 삼각수 외에도 점을 도형의 형태로 배열해 사각수와 오각수, 육각수 등을 만들고 그 점의 개수의 특징을 연구했다. 이처럼 특정한 도형을 가리키는 수들을 ‘도형수’라고 부른다.
학자들은 도형수를 만드는 규칙에 대해 연구해 마치 수열의 일반항처럼 각 도형수를 만드는 공식도 만들었다. 그 중에서 삼각수와 오각수, 육각수를 만드는 공식은 아래와 같다. 

완전수와 사면체수 품은 삼각수

도형수 중에서 삼각수는 가장 기본이 되는 수면서 동시에 ‘완전수’나 ‘사면체수’를 포함하는 다채로운 특징을 가지고 있다. 완전수는 자신을 제외한 약수의 합으로 표현되는 수를 말한다. 예를 들어 6은 약수인 1과 2, 3의 합과 같아 완전수다. 학자들이 연구한 결과 완전수 중에서 짝수인 경우는 모두 삼각수가 된다.
사면체수는 사면체를 이루는 점의 개수를 나타내는 수다. 삼각수가 평면도형의 수라면, 사면체수는 입체도형을 나타내는 수다. 그런데 피라미드 모양의 사면체는 삼각형을 쌓아서 만들 수 있기 때문에 삼각수로도 나타낼 수 있다. 따라서 사면체수를 구하는 공식도 삼각수의 배수 형태로 표현된다.

오일러의 오각수 정리와 페르마의 다각수 정리

스위스 출신 18세기 수학자 레온하르트 오일러는 ‘무한 곱셈 형태’의 수식을 ‘무한 합 형태’에 대한 항등식으로 나타낸 ‘오일러의 오각수 정리’를 다음과 같이 만들었다. 

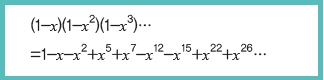
도형수와는 전혀 상관이 없어 보이는데 왜 오각수 정리라는 이름이 붙은 걸까? 오각수의 수열과 오일러의 수식을 잘 비교해 보면 이유를 찾을 수 있다. 등식의 오른쪽인 무한 합으로 표현된 수식에서 미지수 x의 지수에 오각수 수열이  나타나기 때문에 오각수의 정리라는 이름이 붙은 것이다.
한편 페르마의 마지막 정리로 널리 알려진 17세기 프랑스 수학자 피에르 드 페르마는 ‘모든 자연수는 최대 n개의 n각수의 합으로 나타낼 수 있다’는 다각수 정리를 남겼다. 다각수는 2차원 평면 형태의 도형수를 뜻한다.
다각수 정리를 쉽게 설명하면 임의의 자연수는 3개 이내의 삼각수 혹은 5개 이내의 오각수의 합으로 표현할 수 있다는 것이다. 예를 들어 73은 삼각수 36을 두 번 더하고 삼각수 1을 더해 만들 수 있다. 또 오각수 1을 세 번 더한 뒤 오각수 70을 더해 완성할 수도 있다.
페르마는 마지막 정리를 남겼을 때처럼 이 정리를 증명 없이 남기면서 다음에 증명을 하겠다고 했다. 하지만 결국 증명은 남기지 않았다. 이후 프랑스 수학자 조제프 루이 라그랑주와 독일 수학자 카를 프리드리히 가우스가 부분적으로 증명했고, 프랑스 수학자 오귀스탱 루이 코시가 1813년에 증명을 완성했다. 자, 이제 삼각수와 오각수, 육각수를 동시에 만족하는 수를 찾는 문제에 도전해 보자! 

도움 사이냅소프트