d라이브러리

방송을 시작하기 전에 슬픈 소식을 전합니다. 오늘이 수학동아 TV의 마지막 방송입니다. 길면 길고 짧다면 짧은 기간 동안 시청해주신 여러분께 감사 인사를 전하며 오늘 이 한 몸 불태우겠습니다. 마지막 수학 개념은 ‘도형의 닮음’입니다! 

인터넷에 검색해보니 ‘수포자 만드는 수학 개념’ 목록에 ‘도형의 닮음’이 있더군요. 아마 개념은 어렵지 않은데 복잡해 보여서 그런 것 같아요. 수학동아 TV마저 복잡하게 설명하면 시청자들이 전부 달아날 테니 ‘인싸’들의 필수템인 SNS 이야기로 방송을 시작해볼게요.

SNS에 사진을 올릴 때 가장 먼저 무엇을 해야 할까요? 보정도 중요하지만, 우선 크기를 조절해야 합니다. 사진에서 보여주고 싶은 부분이 작으면 크게 확대하고, 사진의 크기가 커서 일부가 잘리면 작게 줄여야 하니까요. 여기에 닮음이 어디 있냐고요? 

여러분이 사진을 확대하거나 축소하면 원래 사진 모양인 사각형과 ‘닮음’인 도형을 계속 만들고 있는 겁니다. 만약 가로세로 중 한 방향으로만 늘이거나 줄였다면 닮음이 아닙니다. 가로세로 비율이 달라져 사진도 이상하게 바뀔 겁니다. 물론 다리가 길어 보이려고 다리 부분만 세로로 길게 늘이기도 하지만요!

사진을 가로세로, 즉 한쪽에 치우치지 않고 크기를 조절해야 원래 모양과 닮음인 사진을 만들 수 있다고 했죠? 그런데 가로세로를 동시에 늘이거나 줄인다고 전부 닮은 건 아닙니다. 정확하게 말하면 가로세로를 같은 비율만큼 늘이거나 줄여야 닮음이지요.

‘비율’이라고 썼다고 어렵게 생각할 필요 없습니다. 쉽게 말해 가로의 길이가 2배 커지면 세로의 길이도 딱 2배 커져야 하고, 3배 커지면 똑같이 3배 커져야 한다는 뜻이니까요. 예를 들어 가로세로의 길이가 각각 2와 3인 사각형과 닮은 사각형을 만들고 싶으면 각각에 같은 수를 곱하면 되는 거예요.

어떤 두 도형이 닮음인지 판단하는 기준이 서로 대응하는 변의 비이기 때문에 닮음과 비는 떼려야 뗄 수 없는 관계입니다. 그래서 두 도형이 닮음이라고 말하려면 대응하는 변의 길이의 비가 무엇인지도 말해줘야 하지요. 

반대로 닮음인 두 도형의 비를 알고 싶으면 서로 대응하는 변 1쌍을 골라 길이를 비로 나타내면 됩니다. 두 도형이 닮음이면 한 도형의 각 변에 똑같은 수를 곱해서 다른 도형이 되므로 아무 변이나 골라도 비가 같거든요. 서로 닮은 두 직사각형의 가로의 길이가 각각 2와 4면 길이의 비는 1:2고, 3과 4면 3:4입니다. 

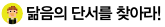
두 도형이 닮음인지 아닌지 판단하려면 우선 모양이 같아야 합니다. 정삼각형은 정삼각형끼리 정사각형은 정사각형끼리만 닮음일 수 있지요. 모양이 같으면 평면도형뿐 아니라 정육면체나 원뿔, 구 같은 입체도형도 닮음일 수 있지요.

어떤 도형들이 서로 닮음인지 판정하는 방법은 대개 비슷하므로 가장 간단한 평면도형인 삼각형을 대상으로 닮음을 판정하는 방법을 살펴보도록 하죠. 삼각형이 가진 성질 때문에 대응하는 세 변의 길이를 일일이 비교하지 않아도 닮았는지 안 닮았는지 알 수 있습니다.

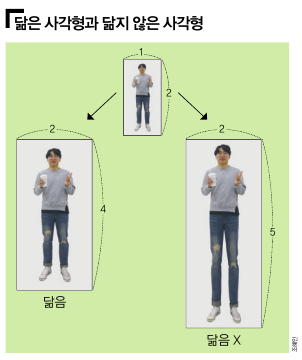
자, 이제 여러분의 날카로운 눈썰미를 발휘할 시간입니다. 눈앞에 보이는 몇 가지 단서를 찾아서 두 삼각형이 닮음임을 알아내야 하니까요. 

첫 번째는 처음 말한 것처럼 삼각형의 세 변의 길이의 비가 서로 같으면 두 삼각형은 닮음입니다. 두 번째는 두 각만 같으면 닮음이라는 겁니다. 여기서 한 가지 추리를 해보죠. 모든 삼각형의 내각의 합은 항상 180°입니다. 두 각의 크기만 같으면 나머지 한 각은 (180-두 각의 합)°이므로 두 각만 같아도 자연스럽게 세 각이 모두 같지요. 

마지막으로 각이 하나만 같고 그 각에 붙어있는 두 변의 길이의 비가 같으면 두 삼각형은 닮음이에요. 한 각을 고정하고 그 각에 붙어있는 두 변의 길이가 똑같은 비율로 늘어나면 나머지 두 각의 크기가 변하지 않기 때문이지요.

이제 우리는 두 삼각형이 닮음인지 알 수 있는 세 가지 방법을 아는 겁니다. 하나는 대응하는 세 변의 길이의 비가 같은지 살펴보는 것(SSS 닮음), 다른 하나는 두 내각의 크기가 같은지 살펴보는 것(AA 닮음), 마지막은 한 각과 그 각에 붙은 변의 길이의 비(SAS 닮음)를 살펴보는 겁
니다.

두 삼각형이 어떤 단서를 줄지는 아무도 모릅니다. 그러니 이 세 가지 방법을 잘 기억해뒀다가 상황에 맞는 방법을 써서 닮음인지 알아봐야 합니다!

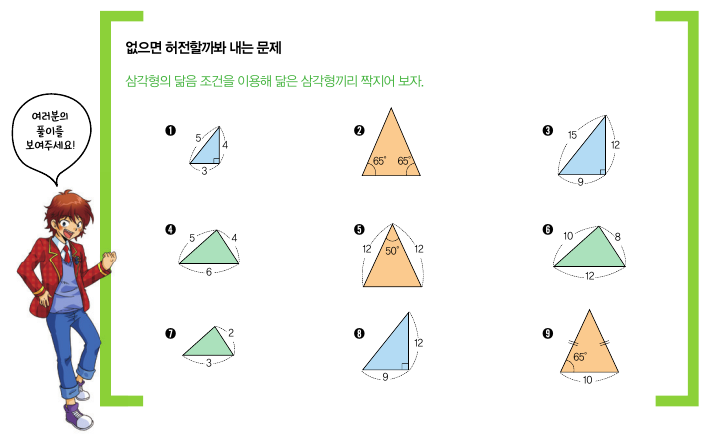
삼각형의 닮음 조건을 이용하면 몇 가지 흥미로운 사실을 찾을 수 있어요. 첫 번째는 모든 정삼각형은 서로 닮음이라는 거예요. 정삼각형의 세 각은 항상 60°니까 세 각이 모두 같아 모든 정삼각형은 닮음이지요. 직각삼각형은 한 각이 항상 90°니까 나머지 두 각 중 한 각만 같아도 서로 닮음입니다. 이등변삼각형은 두 변의 길이가 항상 같으므로 두 이등변삼각형이 닮았는지 알아내려면 길이가 같은 두 변이 만드는 각이 같은지만 살펴보면 됩니다.

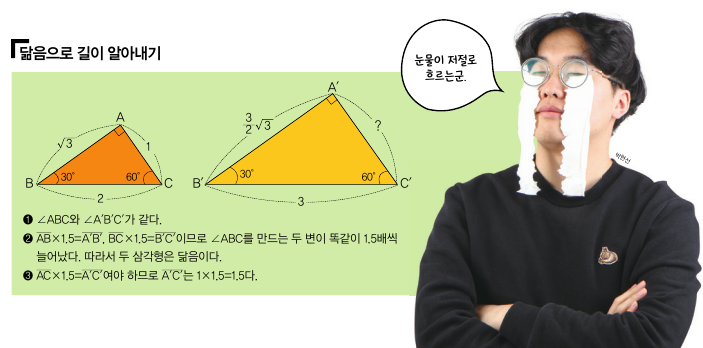
그런데 왜 이렇게 닮음에 집착할까요? 닮음이면 각 변의 길이의 비가 같다는 걸 이용해 길이를 모르는 변의 길이를 대강 추측할 수 있기 때문이에요. 만약 한 삼각형의 세 변의 길이를 알고 다른 삼각형은 한 변의 길이만 안다고 생각해보세요. 자로 직접 재지 않는 이상 죽었다 깨어나도 변의 길이를 알 수 없지만, 두 삼각형이 닮았다면 길이의 비를 알아내서 나머지 두 변도 알아낼 수 있습니다. 도형 문제를 풀 때 무척 유리하겠죠?    

평면도형의 넓이는 보통 도형의 변의 길이를 이용해 구할 수 있어요. 두 도형이 닮으면 변의 길이가 서로 관련 있고 변의 길이는 넓이와 관련 있으니까, 닮은 도형의 길이의 비와 넓이도 관련 있지요. 한 도형의 각 변을 n배 했으면 넓이는 n2배가 됩니다. 그래서 길이가 2배씩 늘어난 도형의 넓이는 무려 22=4배가 되지요.  

아앗…! 어느새 마지막 수학동아 TV 방송이 끝났습니다. 1년 동안 사랑해 준 여러분께 다시 한번 감사 인사드립니다. 비록 BJ맹추는 떠나가지만 아무쪼록 수학 개념을 재밌게 배우길 바라면서 저는 진짜로 떠납니다. 뿅!