d라이브러리

세계대전 당시 유대인은 강제 수용소에서 일하거나 죽음을 맞이하는 일이 잦았습니다. 헝가리 수학자 투란 팔 역시 벽돌공장에서 강제노동했는데요, 그 순간에도 수학 문제를 제기해 지금까지 연구되고 있습니다. 

헝가리의 유명한 수학자 투란 팔은 에르되시 팔과 함께 46년 이상 공동 연구했습니다. 첫 수학 논문 역시 1933년에 에르되시와 함께 쓴 겁니다. 이후로도 좋은 연구를 한 덕분에 1934년 박사학위를 받기 전까지 저명한 수학 학술지에 논문을 여러 편 실었고, 세계적으로 이름을 알렸습니다.

하지만 유대인인 투란은 심한 차별을 받았습니다. 대학에서 연구할 수 있는 자리나 강사 자리는 고사하고 중고등학교 선생님 자리도 구할 수 없었습니다. 돈을 벌기 위해 개인 교습을 하며 수학 연구를 계속 할 수 밖에 없었습니다. 첫 논문을 출판한 지 5년이 지난 1938년 말에야 부다페스트에 있는 어느 학교 수학 선생님 자리를 구합니다. 하지만 이렇게 얻은 직장도 제2차 세계대전이 발발하면서 오래 다니지 못합니다. 1940년 9월, 투란은 유대인이라는 이유로 강제 수용소에 끌려갔거든요.

이곳에서 있었던 일은 1977년 창간한 ‘그래프 이론 학술지(Journal of Graph Theory)’ 첫 호 인사말에 자세히 나와 있습니다. 투란이 직접 본인의 경험담을 적었거든요. 

강제노동 중에도 수학 생각 

강제 수용소에서 일하는 것을 감시하던 장교가 투란의 이름을 우연히 듣고, 수학자냐고 물어봤다고 합니다. 그 장교는 여기에 오기 전 인쇄소에서 교정 보는 일을 했는데, 그때 투란의 논문을 본 것이죠. 그 장교는 본인이 해줄 수 있는 최대한의 배려라면서 목재를 옮기고 있던 투란에게 목재 보관소 관리를 맡깁니다. 

그 후에도 투란은 여러 곳에서 강제노동을 했습니다. 1944년 7월부터는 벽돌공장에서 일했죠. 그 공장에는 벽돌을 굽는 가마와 벽돌 보관장소가 여러 곳에 있었고, 각각 가마에서 보관장소까지는 선로로 연결돼 있었습니다. 투란은 가마에서 벽돌을 꺼내 수레에 담고, 선로를 이용해 수레를 이동시켜 보관장소까지 벽돌을 나르는 일을 했습니다. 일 자체는 그리 어렵지 않았지만, 선로 2개가 교차하는 지점의 수레 운전이 어려웠습니다. 방심하면 벽돌을 떨어뜨리기 일쑤라 투란은 막연하게 교차점의 수가 줄어든다면 편할 것이라고 생각했습니다. 그리고 다음과 같은 문제를 떠올렸습니다.

투란은 며칠간 이 문제를 생각했지만, 어려워서 정확한 답을 구하지 못했습니다. 그런데 투란이 강제노동하지 않았다면, 그의 수학은 영영 못 봤을 수도 있습니다. 헝가리에 있던 유대인이 강제노동 자리를 못 받은 경우 대부분 독일의 아우슈비츠 강제 수용소 같은 곳에 보내져 죽었기 때문입니다. 헝가리에 있던 유대인 75만 명 중 55만 명이 학살당했다고 합니다. 

전쟁이 끝난 뒤 1949년 투란은 헝가리 외트뵈시 로란드대학교에서 1976년 생을 마감할 때까지 교수로 지냈습니다. 1952년에 결혼한 부인 역시 조합론을 전공한 수학자 베러 쇼시입니다. 쇼시는 2002년 포스텍에서 열린 한국, 헝가리 조합론 공동 워크숍에 참석하기도 했습니다.

한편 1952년 투란은 폴란드를 처음 방문했고, 그때 벽돌공장 문제를 강연에서 발표했습니다. 거기서 문제를 들은 폴란드 수학자 카지미에시 자란키에비치는 곧 이 문제를 해결했다고 생각했습니다. 

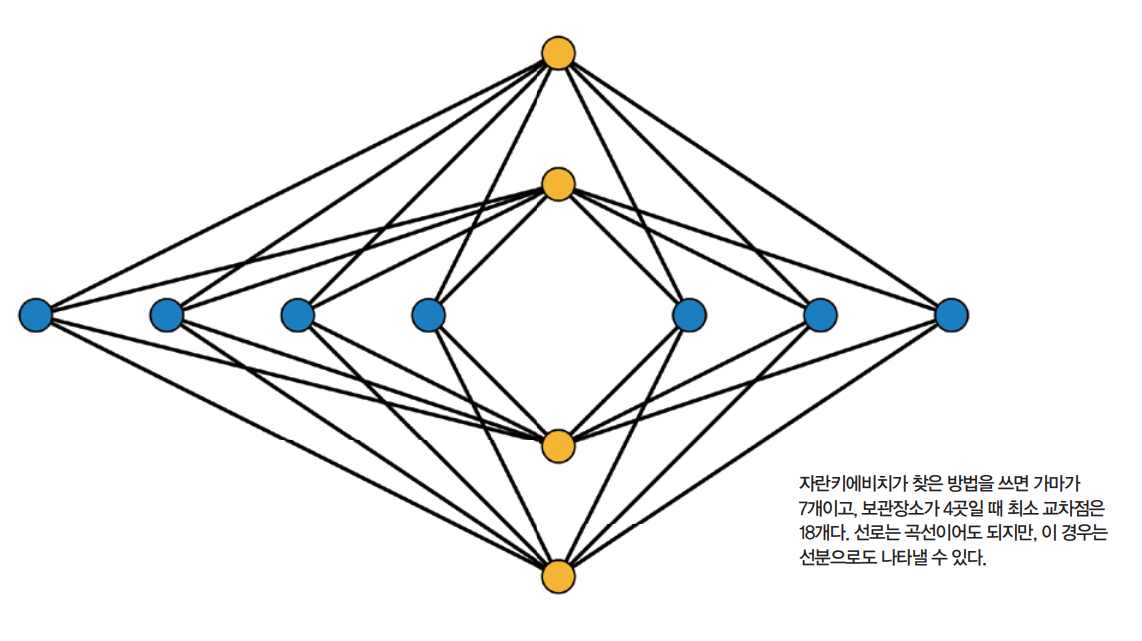
자란키에비치는 가마가 m개, 보관장소가 n곳일 때 가마를 가로로 일렬 배치하고, 가운데 가마에서 조금 떨어진 곳에 수직으로 보관장소를 배치하면 이때 교차점의 수인 x가 최소라고 발표했습니다. 

하지만 11년 뒤 그 증명에 오류가 있다는 것이 발견됩니다. 그때는 이미 자란키에비치가 세상을 떠난 뒤였지요. 

현재까지 n≤6일 때, n≤8이면서 m≤10일 때 옳다는 게 알려져 있습니다. n=7일 때는 최솟값이 저 값의 0.979배 이상이라는 것만 밝혀져 있습니다. 아직 0.979를 1로 만들지는 못한 셈이죠.

벽돌공장 문제 일반화는 NP-난해 

이제 이 문제를 일반화해 봅시다. 총 n개의 장소가 있고, 어느 두 장소를 선로로 이을지 말지를 미리 결정해 놨습니다. 이때 필요한 교차점 수의 최솟값은 얼마일까요? 

수학에서 말하는 ‘그래프’라는 것이 바로 이렇게 n개의 점과 각 두 점 사이에 관계를 선으로 나타낸 겁니다. 벽돌공장 문제는 m+n개의 점에서 특정 형태로 선이 연결돼 있을 때 최소 교차점 수가 얼마인지 묻는 것이지요.

벽돌공장 문제도 아직 미해결이니, 일반화 문제도 대단히 어렵겠죠? 1982년 미국 컴퓨터 과학자 마이클 가리와 데이비드 존슨이 이 문제가 ‘NP-난해’라는 것을 증명했습니다. 즉 P≠NP라는 추측이 참이라면 이 문제를 효율적으로 다항 시간 안에 구하는 것은 어려울 것이라는 거지요. 

심지어는 선 하나만 지워도 교차점이 없게 그릴 수 있는 그래프에서조차 최소 교차점 수를 구하는 것이 NP-난해라는 것이 밝혀져 있습니다. 

2013년 슬로베니아 수학자 보얀 모하르와 세르기오 차벨로는 P=NP가 아닌 이상, 임의의 상수 c에 대해 최소 교차점 수의 c배 이하인 값을 다항식 시간 내에 찾는 것조차 불가능하다는 것을 증
명했습니다. 

최근 최소 교차점 수를 구하는 게 어렵다는 결과가 하나 더 나왔습니다. 2018년 퍼털 흐린언 체코 마사리코바대학교 교수와 카르스텐 토마센 덴마크공과대학교 교수는 최소 교차점 수가 홀수인지 짝수인지 결정하는 것조차 NP-난해라는 것을 밝혔습니다. 즉 최소 교차점 수가 홀수인지 다항식 시간에 알 수 있다면 P=NP가 돼, 다른 어려운 모든 NP-난해 문제도 모두 다항식 시간에 해결할 수 있게 되는 것이죠. 심지어 임의의 소수 에 대해 최소 교차점 수가 p의 배수인지 결정하는 문제 또한 NP-난해라고 합니다. 

이처럼 어려운 상황에도 수학에 대한 열정을 잃지 않은 투란 덕분에 재미있는 연구 세상이 펼쳐졌습니다. 독자분들도 수학에 대한 열정을 계속 유지하길 바랍니다.