d라이브러리

두리안
두리안(Durian)은 ‘뾰족한 가시’를 뜻하는 말레이어 ‘두리(Duri)’에서 나온 이름이다. ‘두리오’라는 나무에서 자라는 열매를 말하며 그 종류가 무려 30여 가지에 달한다. 그중 약 9가지 종의 열매만 먹을 수 있다고 하는데, 1년에 한 번만 수확할 수 있기 때문에 동남아시아에서도 한두 계절에만 먹을 수 있는 귀한 과일이다.

*문태선 선생님은 베트남 호치민 시의 한국국제학교 수학교사로, 틈날 때마다 주변 나라로 여행을 떠나 매스투어를 즐기고 있다.

‘과일의 여왕’이라 불리는 두리안을 아시나요? 바나나, 망고, 파인애플, 키위, 오렌지, 체리 같은 수입과일이 흔해진 요즘에도 두리안은 여전히 비행기를 타고 동남아로 날아가야만 맛볼 수 있는 낯설고 귀한 과일입니다. 지옥의 냄새와 천상의 맛을 자랑한다는 두리안, 그리고 그에 못지않은 지독한 냄새로 묘한 궁금증을 자아내는 잭푸르트에 숨겨진 수학을 소개합니다.

생김새만 보면 두리안은 먹음직스러운 과일과는 거리가 멀어요. 두리뭉실한 몸통에 뾰족한 가시가 온통 솟아있어 만지는 것부터가 쉽지 않습니다. 더군다나 냄새는 어찌나 지독한지 먹고 싶은 마음이 들기는커녕 가까이 가고 싶지도 않게 만드는 녀석이랍니다. ‘지옥의 냄새’라고도 불릴 만큼 고약한 두리안의 냄새를 동물의 배설물이나 썩은 양파 냄새와 비교하기도 해요. 조금 과장하자면 과일계의 스컹크라 불러도 될 것 같습니다.

그런데 가시로 덮인 두툼한 껍질을 칼로 쪼개고 나면 노랗고 부드러운 속살이 드러납니다. 코를 막고 조금만 용기를 내 그 노랗고 끈적이는 물질을 입에 넣어보면 슈크림보다 더 달달하고 부드러운 맛과 향이 사르르 입안에 퍼진답니다. 영국의 소설가 앤서니 버지스는 “변소에서 바닐라 커스터드를 먹는 것과 같다”고 했는데 정말 기막힌 표현이 아닐 수 없습니다.

두리안과 똑 닮은 과일이 하나 더 있습니다. 바로 잭푸르트입니다. 생김새는 대충 주물러놓은 메주 같고, 크기는 어마어마해서 아주 둔하고 우스꽝스럽답니다. 무게는 보통 10~30kg이고, 큰 것은 40kg까지 나간다고 합니다. 게다가 두리안과 비슷한 냄새가 스멀스멀~ 나는데, 다행히 이 녀석의 냄새는 사과와 파인애플, 망고를 섞어 놓은 듯한 달달함이 느껴져 두리안보다는 덜 역하답니다.

그럼에도 이걸 먹어야 하나 말아야 하나 고민에 빠지게 되는데, 코를 막고 노란 속살을 씹어보면 감 같기도 하고 바나나 같기도 한 달큰함이 쫄깃한 식감과 함께 목으로 넘어갑니다. 한번 맛보면 멈출 수 없는 맛이랄까요? ‘용기 있는 자! 맛있는 것을 먹으리라!’

영화처럼 반전을 경험하게 하는 두리안과 잭푸르트. 이쯤 되면 두리안과 잭푸르트는 과일계의 사촌이라고도 할 수 있겠죠? 그런데 극적인 반전은 여기서 끝이 아닙니다. 방금 속살을 먹기 위해 던져두었던 두리안과 잭푸르트의 껍질. 그 냄새나는 껍질을 다시 가져와 자세히 들여다보세요. 그러면 그 껍질 속에서 맛의 반전을 뛰어넘는 수학적 반전을 발견할 수 있답니다.

잭푸르트

잭푸르트(Jackfruit)는 동남아시아, 아프리카, 브라질 등에서 자라는 열대과일이다. 방글라데시의 국가 과일이기도 하다. 이름은 포르투갈어인 ‘자카(Jaca)’에서 유래했다. 완전히 자란 잭푸르트 나무는 열매를 맺기 위해 수백에서 수천 송이의 꽃을 피우고, 1년에 100~200개의 열매를 맺는다.

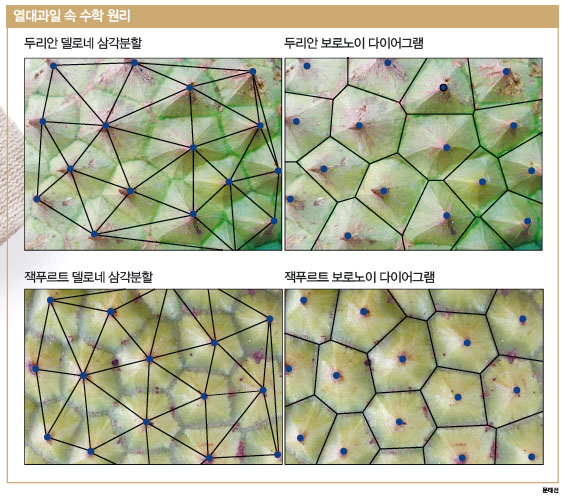
껍질 속 보로노이 다이어그램
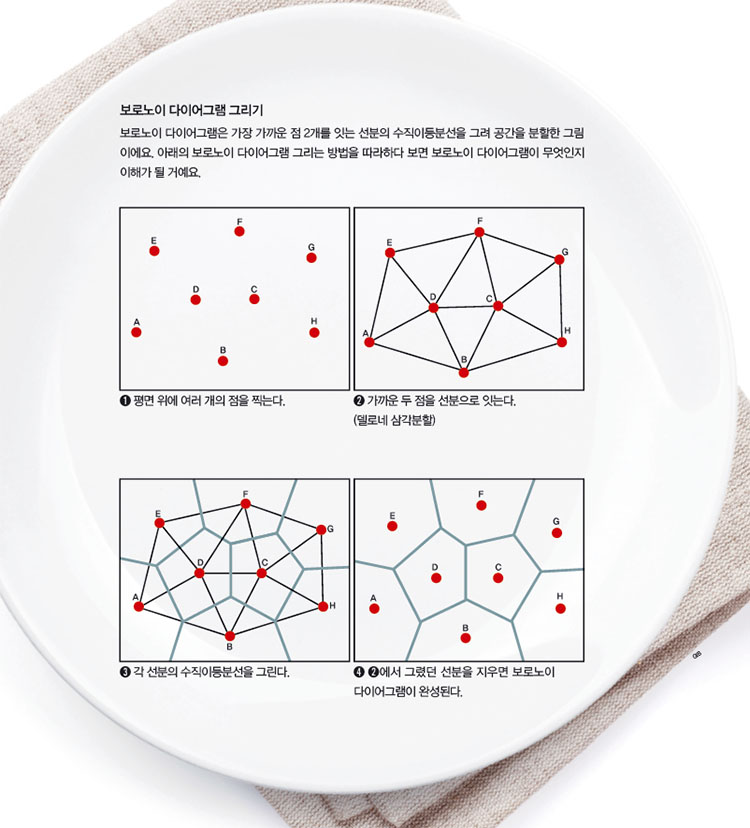
두리안과 잭푸르트의 껍질에서는 보로노이 다이어그램을 찾을 수 있어요. 둥글게 굽은 면 중에서 평평하고 나름 규칙적으로 보이는 면을 찾아 사진을 찍어봅시다. 그리고 앞서 설명한 방법대로 선분과 수직이등분선을 그리면, 정말 놀라운 결과를 눈으로 확인할 수 있습니다.

신기하게도 두 껍질에는 이미 진한 갈색으로 점이 찍혀 있습니다. 그리고 진한 녹색 선이 껍질을 나누고 있지요. 그 선이 보로노이 다이어그램과 일치하는 것을 발견했을 때는 정말 경이로웠습니다.

가만 생각해보니 참 재미있어요. 구린 냄새와 못난 모습으로 사람들이 피했던 과일이 가장 잘 보이는 곳에 수학의 원리를 한껏 뽐내고 있다는 사실 말이에요. 어쩌면 이 두 과일은 세상 모든 것에 수학이 있다는 사실을 말해주고 싶었는지도 모릅니다. 여러분도 한번 찾아보세요. 피타고라스가 말했듯이 모든 것은 수학이니까요.