
‘또봇’, ‘헬로 카봇’, ‘다이노포스’, 그리고 ‘터닝메카드’의 공통점은? 모두 변신하는 로봇이다. 그런데 변신하는 로봇만 있는 게 아니라 변신하는 입체도형도 있다는 제보가 들어왔다! 언뜻 보았을 때는 정십이면체인데 몇 번 만지면 순식간에 정육면체로 바뀐다. 도형이 어떻게 변신하는지 알아보자.
순환하며 변신하는 정다면체
모든 면이 합동인 정다각형으로만 이뤄진 정다면체는 오직 다섯 가지 뿐이다. 정다각형 하나로만 이뤄져야 하며, 다각형 면들이 한 꼭짓점에 모일 때 각도의 합이 360˚보다 작아야 하는 까다로운 조건 때문이다. 정다면체는 비록 다섯 개뿐이어도 정다면체를 적당히 변형하면 또 다른 도형을 만들 어 내거나, 재밌는 특징을 찾아낼 수 있다.
정다면체의 각 면에 대각선을 그어 연결하거나, 모서리의 중심에 점을 찍어 잇거나, 각 꼭짓점을 연결하면 다른 정다면체를 만들 수 있다.
우선 정십이면체를 다른 도형으로 바꿔보자. 정십이면체의 각 면에 <;그림1>;처럼 대각선을 그으면, 모서리가 12개인 정육면체로 변신한다. 비슷한 방법으로 정육면체를 이루는 여섯 개의 정사각형에 <;그림2>;와 같은 방법으로 대각선을 그어 정사면체를 만들 수 있다. 정육면체는 면이 여섯 개이므로, 모서리가 여섯 개인 정사면체를 만들 수 있다.
정사면체는 조금 다른 방법으로 변신한다. <;그림3>;처럼 정사면체의 여섯 개의 모서리 중점에 각각 점을 찍어 선분으로 이어, 꼭짓점이 여섯 개인 정팔면체를 만들어 낸다. 정팔면체는 각 모서리를 1:1.618로 내분하는 점을 이어 정이십면체로 바꿀 수 있다.
정이십면체는 각 면의 중심에 점을 찍어, 이 점들을 꼭짓점으로 하는 정십이면체로 변신할 수 있다. 이렇게 다섯 개의 정다면체가 차례로 변신하며 다시 원래의 도형으로 돌아오는 것을 ‘정다면체의 순환’이라고 한다.
다음 장에서 정육면체에서 정십이면체로 순환 하며 변신하는 정십이육면체를 만들어보자.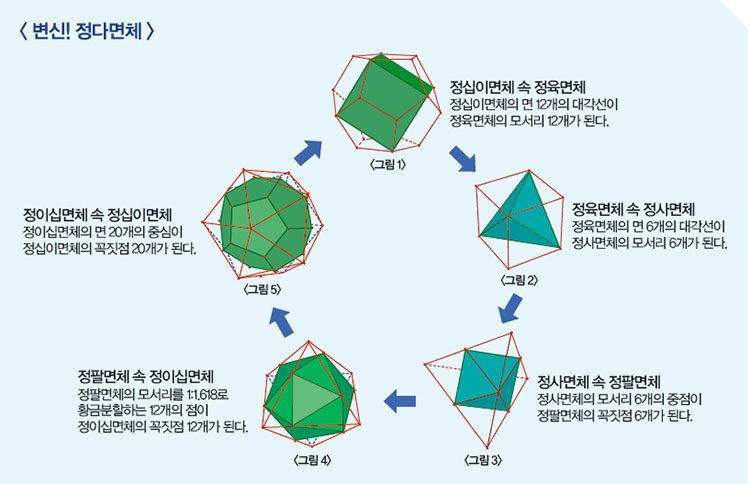



이 기사의 내용이 궁금하신가요?
기사 전문을 보시려면500(500원)이 필요합니다.
2016년 09월 수학동아 정보
글
김영화 부산 온천중 수석교사진행
조혜인 기자
🎓️ 진로 추천
- 수학
- 물리학
- 컴퓨터공학











