d라이브러리

요즘 유행하는 네일아트에 수학을 담아서 설명하면 학생들이 수학을 친숙하게 느낄 수 있을 것이라 생각한다. 테셀레이션에 대한 내용을 학습한 뒤, 친구에게 수학 네일아트를 해 주면서 아름다운 추억을 남겨보자.


우리나라 교육과정에서는 테셀레이션을 다루고 있지 않지만, 미국의 MIC교과서나 핀란드의 교육과정에는 다각형의 성질을 활용한 테셀레이션이 포함돼 있다. 여기서는 테셀레이션을 담은 수학네일아트를 소개하고자 한다.


알람브라 궁전의 패턴 벽화처럼, 동일한 패턴을 반복해 빈틈이나 겹치는 부분 없이 평면을 완전히 채우는 것을 테셀레이션이라고 한다. 화장실의 벽이나 바닥의 타일 배열도 우리 주변에서 쉽게 찾아볼 수 있는 간단한 테셀레이션이다. 우선 테셀레이션의 원리부터 살펴보자.

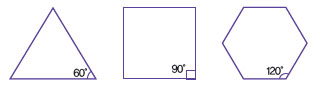
테셀레이션이 만들어지기 위해서는 한 점에 모인 도형의 내각의 합이 360°여야 한다. 단독으로 테셀레이션을 만들 수 있는 정다각형은 정삼각형, 정사각형, 정육각형 세 가지가 있다. 그 이유는 같은 정다각형 여러 개를 한 점에 모았을 때 내각의 합이 360°가 되려면 한 내각의 크기가 360의 약수가 돼야 하는데, 정삼각형(60°), 정사각형(90°), 정육각형(120°)만이 이를 만족하기 때문이다.

그러면 정다각형을 이용해 직접 테셀레이션을 만들어보자. 색종이로 정육각형을 오려 테셀레이션을 만들면 한 점에 모이는 정육각형은 몇 개일까? 3개다. 정육각형이 3개가 모여야 360°가 되기 때문이다. 마찬가지로 삼각형은 6개, 사각형은 4개가 한 점에 모인다.






3. 활동 1 : 다각형에는 어떤 성질이 있는가?

각 모둠에 개인별 활동지를 나눠 주고 다각형의 성질을 찾아보도록 한다.
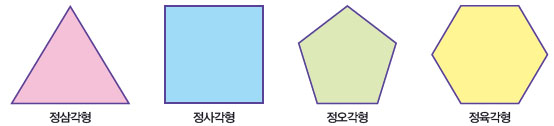
모든 변의 길이가 같고 모든 내각의 크기가 같은 다각형을 정다각형이라 하고, 변의 개수에 따라 정삼각형, 정사각형, 정오각형, …, 정n각형이라고 한다.



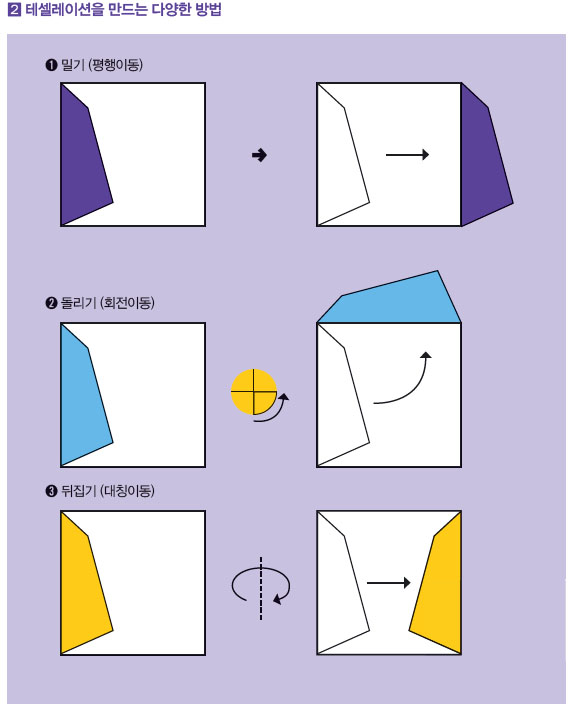
4. 활동 2 : 테셀레이션은 어떻게 만드는가?

활동지로 배부한 정사각형 도안지 위에 학생들이 직접 테셀레이션을 그리면서 평면이동(평행이동-밀기, 회전이동-돌리기, 대칭이동-뒤집기)을 이해하도록 자세히 안내한다. 4인이 한 모둠이므로 테셀레이션 도안을 8절지 위에 완성해 제출할 수 있도록 한다.



다각형의 성질을 배운 뒤 테셀레이션을 담은 수학네일아트 활동을 하면, 학생들은 서로 친구들의 네일아트를 보며 즐거워한다. 지도 교사는 평소 사이가 소홀했던 친구들끼리 자리를 배치해 어색했던 사이가 완화될 수 있도록 분위기를 조성해보는 것도 좋다. 이것은 아이들의 사회성을 기르는 데도 큰 도움이 될 수 있다.