소수의 나눗셈을 자연수의 나눗셈처럼 하기 위해서는 소수점의 위치를 옮겨야 합니다. 이 방법을 왜 쓰는지 알아봅시다. 그리고 새로운 나눗셈 방법도 살펴보겠습니다.

소수는 자연수와 같은 규칙을 따르기 때문에 분수보다 나눗셈 연산을 쉽게 할 수 있습니다. 마치 자연수처럼 나눗셈 연산을 할 수 있기 때문이지요.
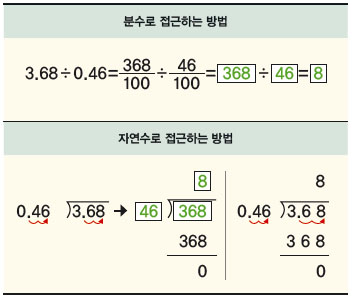
소수는 분수를 위치적 기수법으로 표기한 것입니다. 위치적 기수법이란 숫자가 놓인 위치에 따라 자릿값을 바로 알 수 있는 기수법을 말합니다. 예를 들어, 123에서 1은 백의 자리, 2는 십의 자리, 3은 일의 자리라는 것을 바로 알 수 있죠. 소수의 나눗셈은 위치적 기수법의 장점을 활용해 자연수로 접근해서 해결합니다.
그런데 소수의 나눗셈에서 몫과 나머지를 구할 때는 특별히 주의가 필요합니다. 몫이 자연수로 나타나지 않으면 몫과 나머지가 유일하지 않기 때문입니다. 예를 들어 7.51을 2.8로 나눌 때 몫이 2이고 나머지가 1.91인 경우, 몫이 2.6이고 나머지가 0.23인 경우 등 다양한 몫과 나머지가 나올 수 있습니다.
소수의 나눗셈에서 몫이 자연수로 나누어떨어지지 않을 때는 몫을 분수로 나타내거나 적당한 위치에서
반올림해 근삿값을 구합니다.

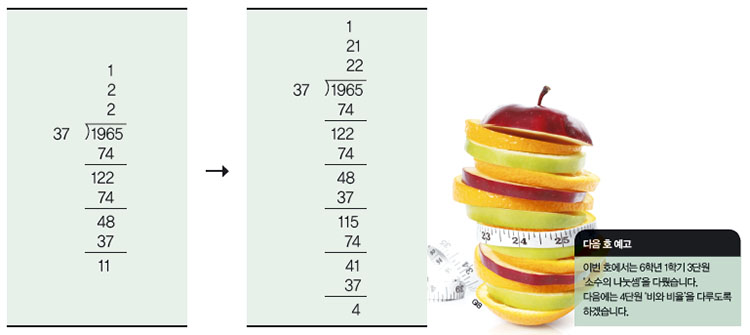
교과서에는 세로로 하는 긴 나눗셈인 장제법만 소개돼 있습니다. 그 외에도 같은 수를 여러 번 빼서 계산하는 누감 알고리즘을 이용해 나눗셈을 할 수 있습니다. 누감 알고리즘은 곱셈이나 나눗셈에 익숙하지 않은 학생들이 나눗셈에 쉽게 접근할 수 있도록 해줍니다. 계산 과정이 눈에 보이기 때문에 계산 오류를 줄일 수 있습니다.
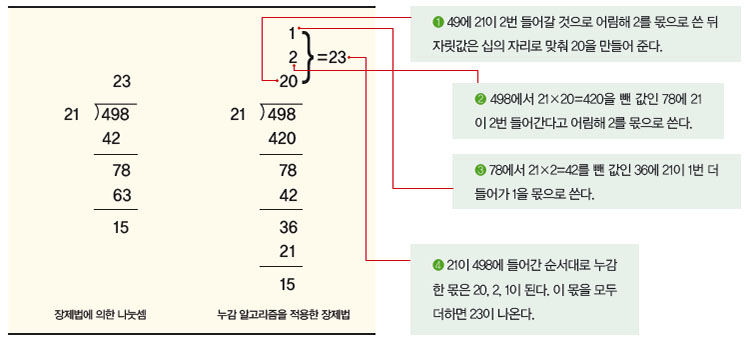
누감 알고리즘을 이용한 나눗셈에서 구구단의 2단이나 3단처럼 계산하기 쉬운 곱셈을 활용하면 나눗셈을 더 쉽게 해결할 수 있습니다. 아래의 예시는 2단을 활용한 나눗셈입니다.