경기 횟수도 많고 이동 거리도 먼 미국 프로야구 메이저리그의 경기 일정은 수학자가 짜는 것으로 유명합니다. 완벽한 일정을 짤 때 ‘조합적 디자인’이라는 수학 분야를 활용하거든요. 그런데 이 분야의 발전은 1850년 영국의 수학 잡지에 실린 퍼즐에서 시작됐습니다.
여학생 15명이 다니는 어느 기숙학교에서는 매일 아침마다 한 줄에 3명씩 5줄로 세워 기숙사에서 교실로 행진한다. 일주일 동안 어느 두 학생도 같은 줄에 2번 이상 서지 않도록 일정을 짜는 게 가능한가?
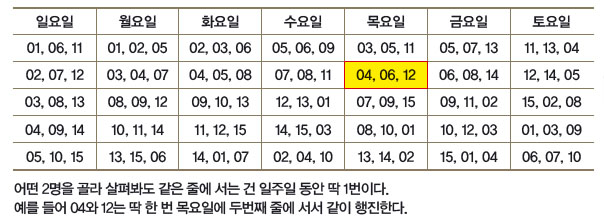
영국 수학자 토마스 커크먼은 1850년 영국의 수학 잡지 ‘신사 숙녀의 일기’에 위와 같은 퍼즐을 소개했습니다. 퍼즐치고는 꽤나 어려운 문제여서 답을 찾기가 쉽지 않습니다. 결국 일반인 독자는 답을 찾지 못했고, 영국 수학자 아서 케일리가 답을 구했습니다. 케일리가 쓴 3쪽짜리 논문은 지금도 인터넷에서 확인할 수 있지요. 이 문제의 정답은 총 7가지인데, 그 중 하나는 다음 표와 같습니다. 여학생 15명을 각각 01부터 15로 나타낸 겁니다.
여학생 15명이 다니는 어느 기숙학교에서는 매일 아침마다 한 줄에 3명씩 5줄로 세워 기숙사에서 교실로 행진한다. 일주일 동안 어느 두 학생도 같은 줄에 2번 이상 서지 않도록 일정을 짜는 게 가능한가?
영국 수학자 토마스 커크먼은 1850년 영국의 수학 잡지 ‘신사 숙녀의 일기’에 위와 같은 퍼즐을 소개했습니다. 퍼즐치고는 꽤나 어려운 문제여서 답을 찾기가 쉽지 않습니다. 결국 일반인 독자는 답을 찾지 못했고, 영국 수학자 아서 케일리가 답을 구했습니다. 케일리가 쓴 3쪽짜리 논문은 지금도 인터넷에서 확인할 수 있지요. 이 문제의 정답은 총 7가지인데, 그 중 하나는 다음 표와 같습니다. 여학생 15명을 각각 01부터 15로 나타낸 겁니다.
(n, q, r) 디자인이 되려면?
날짜를 무시하면 커크먼이 소개한 여학생 문제를 다음과 같이 바꿀 수 있습니다. ‘15명이 각각 3명씩 짝지어 조를 만든다고 할 때 임의의 두 사람이 정확히 한 조에만 속하도록 조를 짤 수 있는가? 이때 한 사람은 여러 조에 속할 수 있다.’ 이를 더 일반화해서 15명이 아니라 n명, 한 조의 구성원을 3명이 아니라 q명, 임의의 두 사람을 r명으로 바꾸면 비로소 ‘(n, q, r) 디자인’이라고 부르는 수학 문제가 됩니다.
(n, q, r) 디자인
n명이 각각 q명으로 구성된 조를 만들 때 임의의 r명이 정확히 한 조에만 속하도록
조를 짤 수 있는 가? 이때 한 사람은 여러 조에 속할 수 있다.
n명이 각각 q명으로 구성된 조를 만들 때 임의의 r명이 정확히 한 조에만 속하도록
조를 짤 수 있는 가? 이때 한 사람은 여러 조에 속할 수 있다.

이 같은 문제를 연구하는 ‘조합적 디자인’은 그 활용도가 높습니다. 스포츠 경기 일정을 효율적으로 짜거나 통신할 때 생기는 오류를 정정하는 부호 체계를 개발하는 데 쓸 수 있거든요.
하지만 최근까지도 어떤 n, q, r값에 대해 그런 디자인이 있는지 정확하게 분류하지 못했습니다. 다만 그런 디자인이 있다면 전체 경우의 수를 따져볼 때 다음과 같은 조건을 당연히 만족해야 한다는 것만 알려져 있었지요.
(n, q, r) 디자인이 있다면 만족하는 조건
➊ n명에서 r명을 뽑는 가짓수는 q명에서 r명을 뽑는 가짓수의 배수다.
➋ 어떤 1명을 뽑아서 그 사람이 속한 조를 따져보면 n-1에서 r-1명을 뽑는 가짓수가 q-1명에서 r-1명을 뽑는 가짓수의 배수다.
➌ 같은 방식으로 0≤i≤r인 모든 정수 i에 대해 n-i명에서 r-i명을 뽑는 가짓수는 q-i명에서 r-i명을 뽑는 가짓수의 배수다.
1970년대 리처드 윌슨 미국 카네기멜론대학교 교수는 n이 충분히 크다면, 이 조건만 만족해도 (n, q, 2) 디자인이 있다는 것을 보였습니다. r>2일 때는 그 후로 30년이 훌쩍 지난 2014년 피터 키바쉬 영국 옥스퍼드대학교 교수가 해결했습니다.
하지만 최근까지도 어떤 n, q, r값에 대해 그런 디자인이 있는지 정확하게 분류하지 못했습니다. 다만 그런 디자인이 있다면 전체 경우의 수를 따져볼 때 다음과 같은 조건을 당연히 만족해야 한다는 것만 알려져 있었지요.
(n, q, r) 디자인이 있다면 만족하는 조건
➊ n명에서 r명을 뽑는 가짓수는 q명에서 r명을 뽑는 가짓수의 배수다.
➋ 어떤 1명을 뽑아서 그 사람이 속한 조를 따져보면 n-1에서 r-1명을 뽑는 가짓수가 q-1명에서 r-1명을 뽑는 가짓수의 배수다.
➌ 같은 방식으로 0≤i≤r인 모든 정수 i에 대해 n-i명에서 r-i명을 뽑는 가짓수는 q-i명에서 r-i명을 뽑는 가짓수의 배수다.
1970년대 리처드 윌슨 미국 카네기멜론대학교 교수는 n이 충분히 크다면, 이 조건만 만족해도 (n, q, 2) 디자인이 있다는 것을 보였습니다. r>2일 때는 그 후로 30년이 훌쩍 지난 2014년 피터 키바쉬 영국 옥스퍼드대학교 교수가 해결했습니다.

그런데 2017년 6월 6일 키바쉬 교수의 결과를 포함한 더 일반적인 연구 결과가 등장했습니다. 영국 버밍엄대학교의 박사 과정생인 스테판 글록과 박사 후 연구원인 앨런 로 박사, 부부인 다니엘라 퀸 교수와 데뤼크 오스투스 교수가 임의의 r명이 어떻게 배치돼 있는지 그 모양까지 고려해 문제를 푼 겁니다. 학술지에 소개된 것은 아니라서 아직 검증이 되지 않았습니다. 만약 오류가 없다면 매우 좋은 연구 결과입니다.
 연구팀 주무기는 ‘확률’
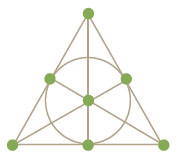
연구팀 주무기는 ‘확률’연구팀은 q명으로 이뤄진 각 조 안에 r명으로 이뤄진 소모임이 있을 때, 전체에서 어떻게 r명을 뽑더라도 그 r명을 소모임으로하는 조가 정확히 하나 있도록 전체를 똑같은 모양의 조로 나눌 수 있는지 연구했습니다. 이를 설명하는 건 매우 어려우니 특수한 경우를 살펴보겠습니다.
q=7, r=3이고, 각 조가 위쪽 그림처럼 7개의 소모임으로 구성돼 있습니다. 각 조의 개개인을 그림의 점에 배치해 같은 선분이나 원 위에 있는 세 사람을 같은 소모임이라고 가정한 겁니다. 연구팀은 전체 n명 중 어떤 3명을 보더라도 정확히 한 조에 그 3명이 소모임을 이루고 있도록 조와 소모임을 짤 수 있는지 알아봤습니다.