
1m의 10억 분의 1, 나노미터. 감히 상상조차 되지 않는 나노미터 세상에 바이러스가 있다. 인류는 아주 오래전부터 바이러스의 영향을 받아왔지만, 그 실체를 눈으로 보게 된 것은 불과 100년도 되지 않았다. 그런데 바이러스의 모양을 관찰해 보니 놀랍게도 기하학적인 구조를 하고 있었다. 인간의 삶을 위협하는 바이러스지만 아름답다는 생각마저 든다. 바이러스는 어떤 기하학 구조를 갖고 있을까?


바이러스는 아주 작고 구조가 단순하다. 얼마나 작은지 보통 현미경으로는 관찰할 수조차 없다. 바이러스의 크기는 1m를 10억 분의 1로 나눈 단위인 ‘나노미터(nm)’로 나타낸다. 종류에 따라 수십에서 수백 나노미터까지 다양하다. 그러나 최근 들어 발견된 판도라 바이러스(1000nm)나 피소 바이러스(1500nm)처럼 큰 바이러스도 있다.
보통 바이러스를 세균과 헛갈리기 쉬운데 세균과는 본질적으로 다르다. 먼저 바이러스는 세균보다 훨씬 작다. 바이러스는 평균적으로 세균의 약 50분의 1정도밖에 되지 않는다. 부피는 길이의 세제곱에 비례하므로 세균 한 마리에 바이러스가 약 12만 5000마리(50×50×50) 들어간다.
간단한 비유를 들면 바이러스가 얼마나 작은지 더 실감할 수 있다. 만약 100나노미터 크기의 인플루엔자 바이러스가 180cm의 성인 남자 키만큼 커진다면, 0.1cm인 개미는 얼마나 커질까? 비례식을 계산하면 개미는 무려 세계에서 가장 높은 산인 에베레스트의 높이(약 8900m)의 두 배 정도가 된다.
구조에서도 바이러스는 세균과 뚜렷하게 다르다. 세균은 살아가는 데 필요한 요소를 모두 갖추고 있지만, 바이러스는 유전정보를 담고 있는 유전체와 유전체를 보호하는 단백질 껍질로 이뤄져있는 비세포성 생물이다. 이 단백질 껍질을 ‘캡시드’라 부른다. 캡시드는 ‘상자(Capsa)’를 뜻하는 라틴어에서 유래한 말이다.
그러나 무엇보다도 바이러스가 세균과 다른 점은 바이러스는 스스로 증식하지 못한다는 점이다. 반드시 다른 동물이나 식물, 세균을 통해서만 증식할 수 있다. 다른 생물에 의존해야만 증식할 수 있다는 뜻이다.



프린시스 크릭과 제임스 왓슨은 구에 가까운 일부 바이러스가 정다면체 중에서도 ‘정이십면체’라고 추측했는데, 여기에는 여러 가지 수학적인 근거가 있다. 먼저 단백질이 서로 결합해 면을 만들려면 사각형이나 오각형보다는 삼각형이 더 견고하다. 삼각형은 세 변의 길이만 정해지면 비틀어지지 않기 때문이다. 또 면과 면이 이루는 각이 클수록 입체가 단단해지므로 정사면체나 정팔면체보다는 정이십면체가 좋다.
크릭은 단백질 3개로 이뤄진 삼각형이 모여 만든 정이십면체 구조 바이러스를 상상했다. 그러면 바이러스에는 많아야 60개의 단백질이 있어야 하는데, 실제로 바이러스는 단백질이 60개보다 많은 경우가 훨씬 많았다. 바이러스의 구조를 정이십면체로 설명하는 데 난관에 봉착한 것이다.
그런데 이 난관은 바이러스와 전혀 상관없는 건축가의 작품으로부터 영감을 받아 풀렸다. 지오데식 돔을 만든 벅민스터 풀러의 제자 로버트 막스는 소아마비 바이러스를 연구하고 있었는데, 삼각형으로 이뤄진 거대한 돔을 보고 단백질이 60개 이상인 바이러스가 지오데식 돔과 같은 형태가 될 수도 있겠다는 생각을 한 것이다.
이후 아론 클루그와 도널드 캐스퍼는 지오데식 돔에서 영감을 받아 연구에 박차를 가한 끝에 1962년 바이러스 캡시드에서 발견한 몇 가지 놀라운 규칙을 세상에 소개했다. 클루그와 캐스퍼 이론의 핵심은 ‘바이러스 단백질 구조를 단일 모양(삼각형)으로 이뤄진 정이십면체 구조로 설명한다는 것’이다. 이때 단백질의 수가 많아져도 꼭짓점이 12개이고 면이 20개인 정이십면체 구조에는 변함이 없다.
예를 들어 순무황색모자이크 바이러스는 아래 그림과 같이 단백질 180개로 이뤄져 있다. 사다리꼴 모양이 단백질 하나에 해당한다. 언뜻 보면 삼각형 면이 20개보다 훨씬 많은데 어떻게 정이십면체인가 의구심이 든다. 그런데 구조를 살펴보면 정이십면체가 보인다. 순무황색모자이크 바이러스의 구조를 가만히 살펴보면 단백질 5개가 모여 오각뿔 모양을 이루는 곳이 있다. 이것을 ‘펜타머’라고 한다. 또 단백질 6개가 모여 이룬 육각뿔은 ‘헥사머’라고 한다. 이때 각 펜타머의 가운데를 꼭짓점이라 생각하고 각각을 연결해 보자. 20개의 삼각형 면으로 이뤄진 정이십면체 구조(빨간선)가 드러난다.
그런데 오각뿔과 육각뿔이 어우러진 다면체라고 하니 생각나는 것이 있다. 바로 ‘축구공’이다. 축구공 무늬는 정이십면체의 꼭짓점을 자른 깎은 정이십면체다. 펜타머를 오각형으로, 핵사머를 육각형으로 보면 순무황색모자이크 바이러스에서 축구공 무늬가 드러난다.


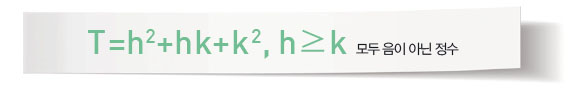
캐스퍼와 클루그가 정이십면체 구조를 제안할 수 있었던 데는 ‘삼각분할’이라는 아이디어가 큰 역할을 했다. 이때 정이십면체의 삼각형은 아래와 같은 식을 따르는데, 이 식에서 T를 ‘삼각분할수’라고 한다.
T 값을 알기 위해 정삼각형 격자가 그려진 평면 위에 정이십면체 전개도를 그려 보자. 아래 그림과 같이 격자의 한 축은 h, 이 축에서 시계반대방향으로 60° 회전한 축은 k이다. 가장 작은 정이십면체의 한 모서리의 길이는 1이므로 h=0, k=1(또는 h=1, k=0)이다. 이때 T=1이다.
그 다음으로 큰 정이십면체는 h=1, k=1이다. 이때 T=3이다. 그런데 T=3일 때의 삼각형의 면적은 T=1일 때의 한 면에 해당하는 삼각형의 정확히 3배다. T 값은 정이십면체의 삼각형 면적과 단위 삼각형과의 관계를 보여준다. T 값은 h와 k의 값에 따라 1, 3, 4, 7, 9,…와 같은 값을 갖는다.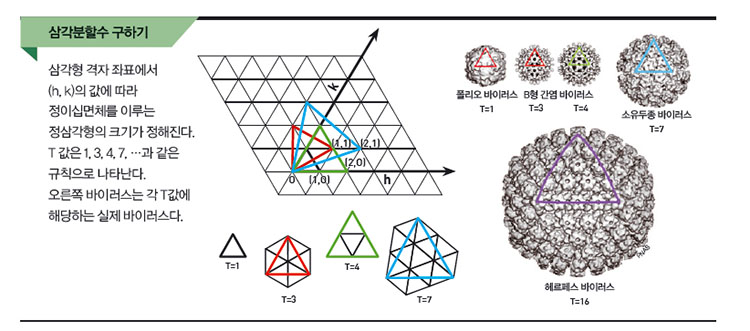
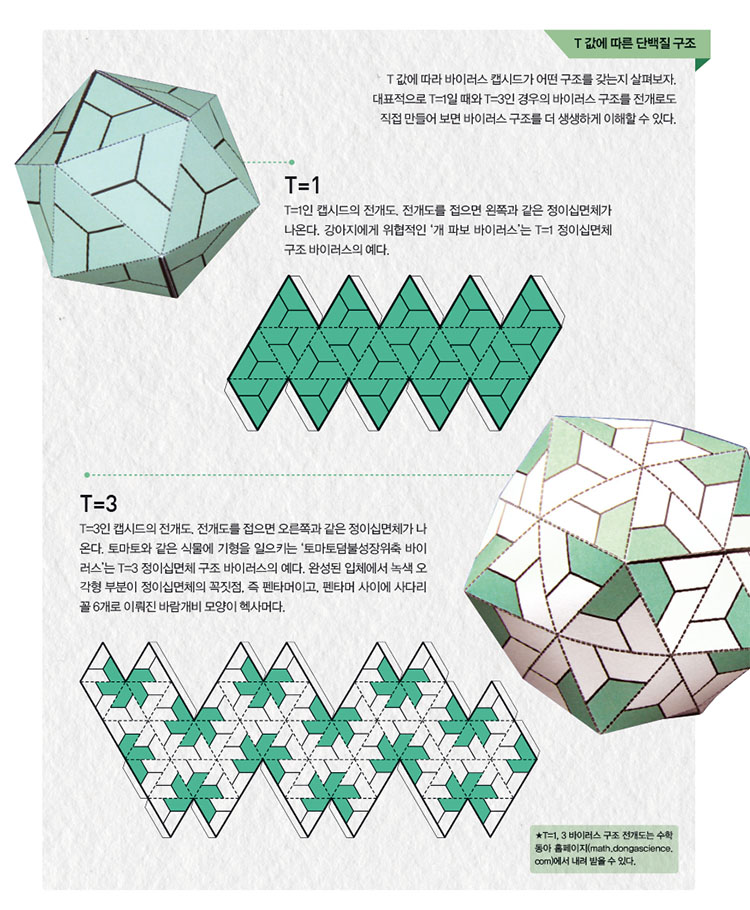


캐스퍼와 클루그 덕분에 일부 바이러스는 정이십면체 구조로 설명할 수있었지만, 여전히 더 많은 바이러스가 남아 있었다. 좀 더 많은 바이러스를 설명할 수 있는 새로운 접근이 필요했다. 21세기에 접어들면서 바이러스 구조에 관한 새로운 이론이 등장했다. 독일의 수리생물학자인 라이둔 트바로크는 2004년 바이러스 기하학에 대한 좀 더 일반적인 이론을 발표했다.
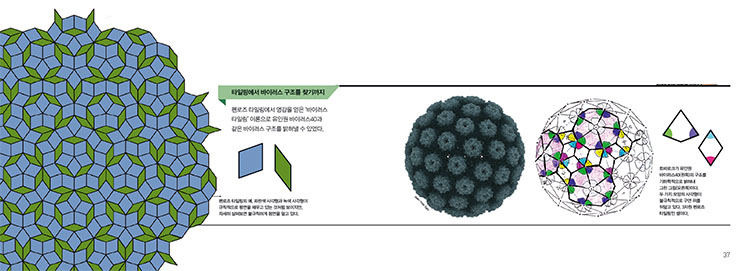
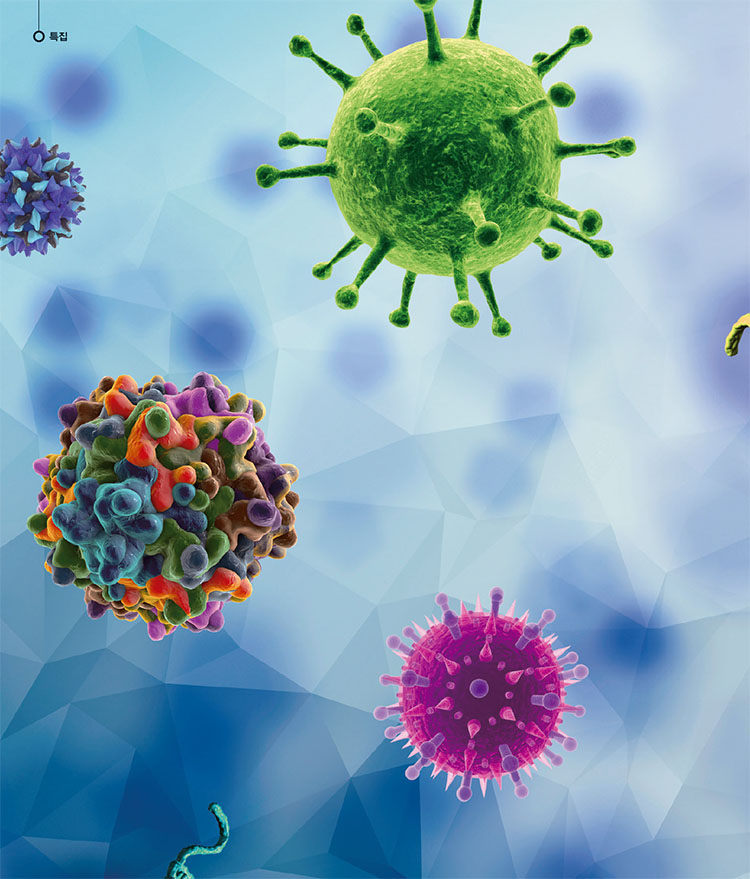
트바로크는 두 가지 이상의 모양으로 이뤄진 바이러스 구조를 제안했다. 마치 구면으로 된 바이러스 캡시드를 단백질 타일로 맞추는 것과 같다고 해서 ‘바이러스 타일링’이라고 부른다. 이 이론은 ‘펜로즈 타일링’에서 통찰을 얻을 수 있다. 펜로즈 타일링은 1974년 영국의 수학자 로저 펜로즈가 발견한 것으로, 언뜻 보면 두 가지 모양의 타일이 규칙적으로 평면을 덮고 있는 것처럼 보인다. 그러나 자세히 보면 불규칙적인 패턴으로 평면을 덮고 있다.
트바로크는 바이러스 타일링 이론으로 ‘유인원 바이러스40’의 구조를 밝혀냈다. 펜로즈 타일링처럼 두 종류의 사각형이 구면으로 된 캡시드를 불규칙적으로 채우고 있다. 트바로크의 바이러스 타일링 이론의 밑바탕에는 대수학의 ‘정이십면체 군’ 이론이라는 고도의 수학 이론이 깔려있다.
‘군(Group)’이란 대수학에서 쓰이는 중요한 수학 개념으로 쉽게 말해 정이십면체 군은 정이십면체가 가지고 있는 대칭의 모임을 수학적으로 나타낸 것이다. 수학의 여러분야 중에서도 순수 수학에 속하는 대수학이 바이러스의 구조를 표현하는 데 핵심적인 역할을 한 것이다.
지금도 많은 과학자들은 바이러스 타일링 이론과 더불어 바이러스의 구조를 알기 위한 연구를 지속해오고 있다. 생물학자들만의 영역이라고 생각하기 쉽지만, 물리학자는 물론 생물학과 거리가 멀어 보이는 수학자도 함께 말이다. 비록 지금까지 밝혀진 바이러스 구조는 거대한 바이러스 빙산의 아주 일부분이지만, 앞으로 더 많은 바이러스 구조가 밝혀질 것이다. 그때 수학은 가장 간결하고 명쾌한 방법으로 자연의 신비를 드러내지 않을까.