d라이브러리

그런데 최근 들어 부쩍 나에게 관심을 가진 사람들이 있어. 바로 수학자들이지. 수학자들은 왜 나한테 관심을 갖는 걸까?


몸집이 커진 뱀의 기하학, 허물

뱀은 혐오동물 중 하나지만, 지혜를 가진 신령스러운 동물로 손꼽힌다. 옛 우리 선조들은 몸뚱이 전체가 한 번에 허물을 벗는 모습을 보고 뱀이 초능력을 발휘한 것으로 믿었다. 이런 뱀의 능력을 신통하게 여겨 재물을 관리하는 신으로 모시기도 했다. 대개 집집마다 뒷마당 장독대에 숨어사는 구렁이를 키웠는데, 이를 ‘업’이라는 신으로 섬겼다. 구렁이가 집 밖으로 나가면 집이 망한다고 걱정할 정도였다.

뱀이 허물을 벗는 모습을 보고 관심을 가진 또 다른 사람은 수학자들이다. 몸을 둘러싸고 있는 비늘을 어떻게 한꺼번에 벗어낼 수 있는지 궁금했기 때문이다. 사실 뱀의 비늘은 전체적으로 한 장으로 돼 있다. 따라서 정상적으로 탈피하면 허물은 조각난 부분이 없이 한 장으로 이루어진다.

이것이 가능한 이유는 수학적으로 설명이 가능하다. 뱀은 비늘이 얇은 쪽부터 몸집이 커진다. 뱀의 비늘은 2겹으로 이루어져 있는데, 몸이 자라면서 둘 중 안쪽 비늘이 함께 성장해 기존에 있던 비늘을 밀어내며 허물을 벗는다. 그런데 뱀은 몸이 먼저 자라고 이후에 비늘이 자란다. 즉, 외부를 둘러싸고 있는 비늘보다 안에 있는 몸통이 먼저 커지는 것이다. 그 결과 비늘은 자연스럽게 한쪽 방향으로 구부러지면서 나선형으로 자라게 된다. 만약 비늘이 일자로 곧게 생기면 뱀이 비늘을 빠져나오기 힘들어 군데군데 구멍을 내야 한다. 하지만 나선형인 덕분에 한꺼번에 몸을 바깥으로 빼낼 수 있다.

그런데 더 놀라운 사실은 뱀의 비늘에서 볼 수 있는 나선이 그 유명한 아르키메데스 나선이라는 점이다. 고대 그리스의 수학자 아르키메데스는 당시 그리스의 3대 난제였던 ‘원과 넓이가 같은 정사각형의 작도’와 ‘임의의 각을 삼등분 하는 작도’ 문제를 해결하기 위해 나선을 연구했다. 그 결과 평면에서 같은 시간 동안 일정한 속도로 회전했을 때 그려지는 곡선을 발견했다. 이것을 아르키메데스의 나선이라고 한다.

뱀의 걸음걸이는 사인곡선!

뱀은 긴 몸을 꿈틀거리며 옆으로 미끄러지듯이 움직인다. 이런 특이한 뱀의 걸음걸이는 일찍이 과학자들의 시선을 사로잡았다.

미국 조지아공대 데이비드 후 교수팀은 비교적 작고 온순한 뱀인 퍼블란밀크 스네이크를 마취시킨 뒤, 뱀의 몸통을 앞, 뒤, 옆으로 기울여 각 방향의 마찰력을 측정했다. 그 결과 앞 방향의 마찰력이 가장 작았고, 옆 방향이 가장 컸다.

뱀은 이동을 하기 위해서 근육을 수축하고 이완하기를 반복하는데, 이때 마찰력이 큰 몸통의 옆쪽이 제동장치의 역할을 해서 머리와 꼬리가 먼저 움직이고 나중에 몸통이 움직이게 된다. 그 결과 S자 모양의 사인곡선 형태로 이동한다.

실제로 대부분의 뱀이 지나간 자리를 보면 사인곡선이 그려져 있는 것을 확인할 수 있다. 뱀의 이런 이동방식은 수영을 하는 데도 도움을 준다. 파도를 따라 사인곡선으로 이동하면, 이동하는 데 쓰는 에너지를 아낄 수 있다.

그런데 특정 지역에 사는 뱀은 사인곡선이 아니라 다른 형태로 이동하기도 한다. 주로 모래땅에서 사는 뱀은 일반적인 뱀과 반대로 이동한다. 먼저 머리와 꼬리를 지지대로 쓰면서 몸통을 옆으로 미끄러뜨린다. 다음에 머리와 꼬리를 몸통 쪽으로 당겨 이동한다. 이 때문에 쉽게 모래를 판다. 한편 사막에 사는 한 방울뱀은 나선형으로 이동한다. 뜨거운 모래와 닿는 걸 가능한 줄이기 위해서 용수철처럼 몸을 감은 뒤 이동하는 것이다.

이처럼 과학자들이 뱀의 이동에 관심을 갖는 이유는 뱀의 이동 원리를 이용해 로봇을 만들기 위해서다. 실제로 뱀의 긴 몸과 사인곡선으로 이동하는 것을 이용해, 나무나 기둥을 기어오르는 로봇이 이미 개발되었다. 이 로봇은 바퀴로봇이 갈 수 없는 좁은 공간이나 기둥 위를 올라갈 수 있어 수색이나 구조작전, 폭발물 탐지 등에 쓰인다.
 
뱀과 함께 즐기는 수학 퍼즐

수학 퍼즐 중에는 유난히 뱀과 관련된 퍼즐이 많다. 뱀의 긴 몸을 이용하면 다양한 도형을 만들 수도 있기 때문이다. 뱀과 관련된 수학 퍼즐을 풀면서 수학적 사고력도 키우고, 무섭고 혐오스러웠던 뱀과도 친해져 보자~!

다각형 안에 뱀을 그리는 뱀 퍼즐

정사각형, 정오각형 등 정다각형 안에 지그재그로 연결된 선을 긋는 뱀 퍼즐은 2003년 미국 스테트슨대 수학과 교수 에릭 프리드만이 고안한 것이다. 새로운 형태의 뱀 퍼즐을 만들어 홈페이지(mathpuzzle.com)에 등록하면, 그 퍼즐은 자신의 이름으로 불리는 영광을 누릴 수 있어 인기가 높다.

뱀 퍼즐은 주어진 도형 안에 일정한 길이와 각도를 가진 선분으로만 이루어진 경로를 만드는 것이다. 예를 들어, 한 변의 길이가 4cm인 정사각형 안에 선분의 길이가 2cm인 선분을 이어 뱀 퍼즐을 만든다고 가정하자. 그러면 문제를 푸는 사람은 스스로 두 선분이 이루는 각도를 하나로 정한다. 만약 45°라고 정했다면, 두 선분이 이루는 각도가 45°의 배수가 되도록 선분을 이어나가면 된다.
 
보드게임으로 즐긴다! ‘뱀과 사다리’

‘뱀과 사다리’는 2명 이상이 하는 보드게임으로, 일반적으로 1부터 100까지 써진 숫자판에 주사위 하나를 굴려 그 수만큼 해당하는 칸을 이동하는 규칙을 따른다. 이때 뱀을 만나면 뱀을 따라 쭉 내려가고, 사다리를 만나면 사다리를 타고 올라간다. 보통 사다리에는 친구를 도와 주는 선행이 그려져 있는데, 그 행동을 해야 다음 단계로 넘어간다. 뱀에는 친구를 괴롭히는 악행이 그려져 있으며, 해당하는 벌칙을 받아야 다음 단계로 넘어간다. 이렇게 뱀과 사다리를 이동하며 칸을 돌다가 100에 먼저 도달하는 사람이 이긴다.

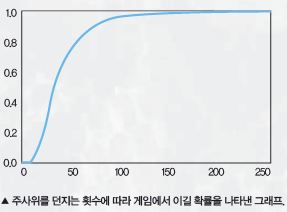
그런데 뱀과 사다리에서 누가 이길지 수학적으로 예측하는 방법은 없을까? 뱀과 사다리는 주사위를 던져 칸을 이동한다. 주사위 던지기는 처음 주사위를 던졌을 때 눈금이 나올 확률과 두 번째로 던져서 나오는 눈금의 확률이 서로 영향을 주지 않기 때문에 마르코프연쇄로 미래를 예측할 수 있다. 마르코프연쇄는 과거와 미래가 서로 영향을 주지 않을 때 미래를 예측하는 방법이다.

뱀과 사다리에선 크게 세 가지를 고려해야 한다. 주사위를 던지는 횟수와 주사위를 던졌을 때 특정 눈금이 나올 확률, 뱀이 있는 칸에 걸릴 확률이다. 뱀이 있는 칸에 걸리면 왔던 길을 되돌아가기 때문에 이를 조건에 반영해야 한다.

실제로 이 조건을 고려해 계산하면 주사위를 던지는 횟수에 따라 게임에서 이길 확률을 구할 수 있다. 그 결과 50회는 넘게 주사위를 굴려야 게임에서 이길 확률이 50%를 넘는다.
 
뱀 이름을 딴 수학이론

놀랍게도 수학이론 중에는 뱀이라는 말이 들어간 정리가 여러 개 있다. 대표적인 예로 대수학의 한 분야인 호몰로지 대수에서 중요한 역할을 하는 ‘뱀 보조정리’를 들 수 있다.

호몰로지 대수는 서로 다른 함수에서 비슷한 역할을 하는 원소들 사이에 이루어지는 대응관계를 연구하는 학문이다. 여기에는 수열의 관계를 함수로 표현하는 ‘완전열’이라는 개념이 있다. 완전열을 만들기 위해서는 함수들의 관계를 그림으로 나타내는데, 이때 그림의 생김새가 뱀을 닮았다고 해서 수학자들이 뱀 보조정리라고 이름 붙였다.

한편 확률론 이론에는 ‘뱀의 눈’이라는 용어가 있다. 이름만 들으면 날카로운 뱀의 눈이 떠올라 왠지 어려운 내용일 것이라는 생각이 든다. 하지만 생각보다 쉽다. 바로 주사위 2개를 던졌을 때 둘 다 1의 눈이 나오는 경우를 뱀의 눈이라고 부르는 것이다.

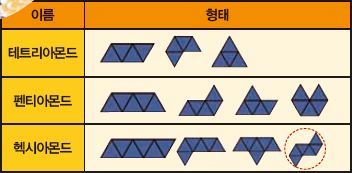
사실 뱀의 눈은 주사위를 던져서 하는 도박에서 유래됐다. 보통 게임에서는 주사위를 던졌을 때 큰 수가 나와야 이길 가능성이 높다. 그런데 주사위에서 가장 작은 수인 1이 두번 나오면 그 사람의 처지가 깊은 산속에서 뱀의 눈과 마주친 것과 같이 암담하다고 해서 ‘뱀의 눈’이라고 부르게 된 것이다. 뱀이 들어간 용어는 기하학 분야에도 있다. 합동인 정삼각형 여러 개를 변끼리 연결하면 새로운 도형이 만들어지는데, 정삼각형이 1개면 모니아몬드, 2개면 다이아몬드, 3개면 트리아몬드, 4개면 테트리아몬드, 5개면 펜티아몬드, 6개면 헥시아몬드라고 부른다. 그런데 헥시아몬드 중에는 마치 뱀이 몸을 구부리고 있는 것처럼 보이는 특정한 모양이 있다. 이걸 뱀과 닮았다는 뜻에서 ‘뱀 폴리아몬드’라고 부른다.
 
뱀으로 무한과 차원, 우주를 표현하다

뱀으로 무한한 우주를 표현할 수도 있을까? 유명한 네덜란드의 화가 마우리츠 코르넬리스 에셔는 뱀으로 다양한 수학을 표현했다.

먼저 에셔의 생애 마지막 작품인 <;뱀>;부터 살펴보자. 세 마리의 뱀이 여러 개의 원 고리 사이에 엉켜 있어, 마치 하나의 매듭을 짓고 있는 것처럼 보인다. 이 작품은 놀랍게도 무한을 주제로 한 것이다. 자세히 보면 그림의 중심으로부터 아주 작은 고리가 점점 커졌다가, 그림의 가장자리에 가면 다시 작아지는 것을 볼 수 있다. 이것은 어떤 도형이 무한히 작아지는 것을 표현한 것이다. 여기서 뱀은 이런 무한 도형을 둘러싸고 있는 우주다. 즉, 에셔는 뱀을 이용해 평면에 무한한 우주를 담으려고 한 것이다.

에셔는 자신의 작품에서 도마뱀을 자주 사용했는데, 그 이유는 평면을 빈틈없이 메우는 테셀레이션을 하기에 적합하기 때문이다. 테셀레이션이 가능한 정다각형은 정삼각형, 정사각형, 정육각형뿐이다. 그는 정육각형 구조의 도마뱀을 그린 뒤 평행과 회전, 대칭이동을 이용해 테셀레이션했다. 그 중에서도 <;도마뱀>;은 차원을 주제로 한 작품이다.

“가상과 현실의 세계를 넘나드는 것을 표현하기 위해서 2차원에 있던 도마뱀이 스케치북을 뚫고 나와 3차원의 실제 도마뱀이 되는 모습을 그렸습니다. 이 도마뱀은 책과 삼각자를 지나 12면체에 도달하는데, 여기서 현실 세계에 도착했다는 성취감을 느낍니다. 스케치북에 그려진 도마뱀에서 대칭도 찾아볼 수 있습니다. 수학에서 대칭은 평행이동이나 회전이동, 대칭이동을 했을 때 원래 모양으로 되돌아오는 것을 말합니다.”