d라이브러리

“새해 첫 날, 이렇게 가족 모두가 모이니까 참 좋구나. 하하! 1월엔 하나 생일이 있지? 10일이 생일이니까 올해는 화요일이구나.”
“맞아요! 생일 선물 꼭 사 주셔야 돼요!”
“물론이지. 그나저나 오늘은 새해 첫 날이니까, 우리 가족만의 특별한 달력을 만들어 보자꾸나. 아빠가 미리 준비해 놨단다!”


면이 12개인 입체도형 모여라~!

2012년 새해가 왔다. 가족과 함께 새 달력을 꺼내 서로의 생일을 찾아보고, 올해 설날과 추석이 언제인지도 찾아보자. 이렇게 유용한 달력을 더 특별하게 만들 수는 없을까?

1년은 12달이므로, 면이 12개인 입체도형을 이용하면 특별한 달력을 만들 수 있다. 면이 12개인 입체도형에는 어떤 것이 있을까?
 
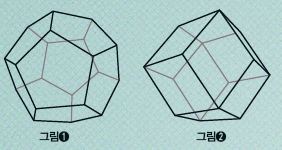
가장 대표적인 십이면체로는 그림❶과 같은 정십이면체가 있다. 정십이면체는 정오각형 12개로 이뤄진 입체도형으로, 정다면체 중 하나다. 정다면체는 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체로 모두 5가지가 있다.

또 다른 십이면체로는 그림❷와 같은 마름모십이면체가 있다. 마름모십이면체 역시 정십이면체처럼 모든 면이 합동이다. 그러나 마름모십이면체는 정다면체라고 부르지 않는다. 그 이유는 꼭짓점에서 만나는 면의 개수가 모두 같지 않기 때문이다. 정오각형으로 이뤄진 정십이면체는 꼭짓점에서 만나는 면의 개수가 3개로 모두 같지만, 마름모십이면체는 꼭짓점에서 3개 또는 4개의 면이 만나 그 개수가 모두 같지 않다.

마름모십이면체는 ‘카탈란다면체’라 부르는 입체도형 중 하나다. 카탈란다면체란, 아르키메데스가 정리한 13가지 준정다면체의 쌍대다면체다. 여기서 준정다면체는 정다면체의 꼭짓점 부분을 깎아내거나 정다면체의 면 사이를 정삼각형으로 채워 만든 다면체를 말한다. 이 준정다면체 각 면의 중심을 꼭짓점으로 이어 만든 다면체가 바로 쌍대다면체다.

따라서 준정다면체의 쌍대다면체인 카탈란다면체 역시 13가지다. 마름모십이면체는 준정다면체 중 깍은 정팔면체의 쌍대다면체다.


마름모십이면체를 닮은 석류 씨앗

“미녀는 석류를 좋아해~♬”
한때 유행했던 음료 광고 노래다. 빨간 석류 씨앗을 입 안에 넣으면, 톡 하고 터져 새콤한 향이 입안을 가득 채운다. 그런데 석류를 먹을 때, 속이 꽉 찬 석류 씨앗을 자세히 본 적이 있을까? 석류 씨앗을 자세히 관찰해 보면 그 모양이 독특하다는 걸 알 수 있다.

빈틈없이 속이 꽉 찬 석류 씨앗은 달력을 만든 마름모십이면체와 그 모양이 비슷하다. 그렇다면 석류 씨앗은 왜 마름모십이면체를 닮은 걸까? 그 이유는 마름모십이면체가 공간을 빈틈없이 채울 수 있는 입체도형이기 때문이다.

입체도형으로 공간을 빈틈없이 채우려고 할 때, 정육면체나 직육면체와 같이 직각인 입체도형이라면 쉽게 틈이 생기지 않게 공간을 채울 수 있다. 그러나 구처럼 둥근 입체도형이나 각이 직각이 아닌 입체도형이라면? 빈틈이 생기지 않게 공간을 메우는 것이 좀처럼 쉽지 않다.
 
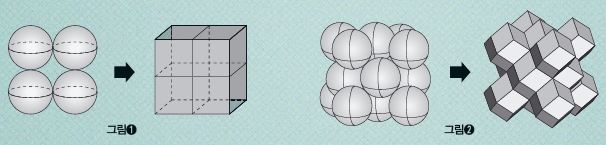
독일의 천문학자 케플러는 다면체 연구에도 많은 공을 세웠다. 어느 날 그는 구 모양의 입체도 형이 공간을 빈틈없이 채우려면 어떤 모양이어야 할지 생각했다.

먼저 그림❶과 같이 구 위에 또 다른 구를 수직으로 쌓은 상태에서 구가 팽창하면, 구는 정육면체가 된다. 또 육각형 모양으로 쌓은 상태에서 구가 팽창하면, 구는 육각기둥이 된다.

한편 석류 씨앗은 처음에 그림❷와 같이 배열돼 있다가, 씨앗이 점점 자라나 팽창하면서 씨앗이 열매 속을 빈틈없이 채운다. 케플러는 이 때 생기는 입체도형이 마름모십이면체와 닮았다는 걸 알아냈다.

이제 석류를 먹을 때, 씨앗을 유심히 관찰해 보자. 속이 꽉 찬 열매를 맺으려고 애쓴 석류의 마음이 느껴질 것이다.