d라이브러리

삼각형에는 여러 가지 중심이 있다. 삼각형의 성질에 따라 서로 다른 성격의 중심을 찾을 수 있기 때문이다. 이번 호에서는 삼각형의 중심으로 가장 잘 알려진 무게중심과 내심, 외심을 집중적으로 알아보자. 물론 색종이를 이용한 활동이다!


직각삼각형의 중심
 

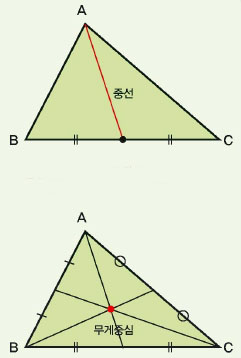
‘삼각형의 중심’을 대표하는 무게중심은 삼각형의 세 *중선이 만나는 점을 말한다. 무게중심부터 살펴보자.

색종이는 정사각형이므로, 한쪽 대각선을 중심으로 반을 접으면 직각이등변삼각형이 된다.그렇다면 직각삼각형의 무게중심은 어떻게 찾을 수 있을까?
 

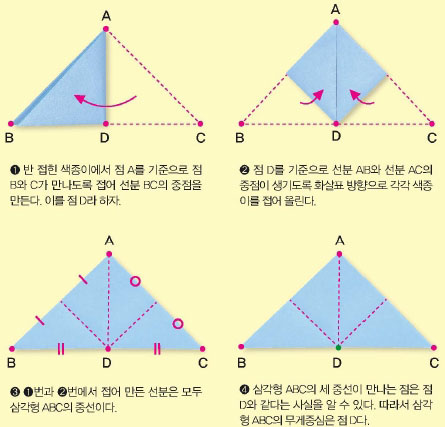
색종이 접기 활동을 할 때, 자주 활용하던 접기 방법에 삼각형의 무게중심이 숨어 있다는 사실이 놀랍지 않은가? 여기서 끝이 아니다. 

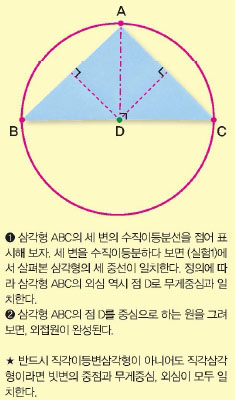
외심이란 삼각형 세 변의 수직이등분선이 만나는 점을 말한다. 삼각형의 세 꼭짓점과 접하는 원을 외접원이라고 하고, 그 원의 중심을 외심이라고 한다. 이 정의를 따라 색종이를 접으면 특별히 직각삼각형은 무게중심과 외심이 같다는 걸 확인할 수 있다.

내심은 삼각형 세 내각의 이등분선이 만나는 점을 말한다. 삼각형 안쪽에 접하는 원을 내접원이라고 하고, 그 원의 중심을 내심이라고 한다.
 

이등변삼각형의 중심

직각삼각형은 한 내각의 크기가 90°인 특수한 경우다. 그렇다면 다른 삼각형의 중심은 어떻게 찾을 수 있을까? 색종이를 오리지 않고 만들 수 있는 이등변삼각형을 접어서 삼각형의 종류에 따라 중심이 어떻게 달라지는지 살펴보자.
 

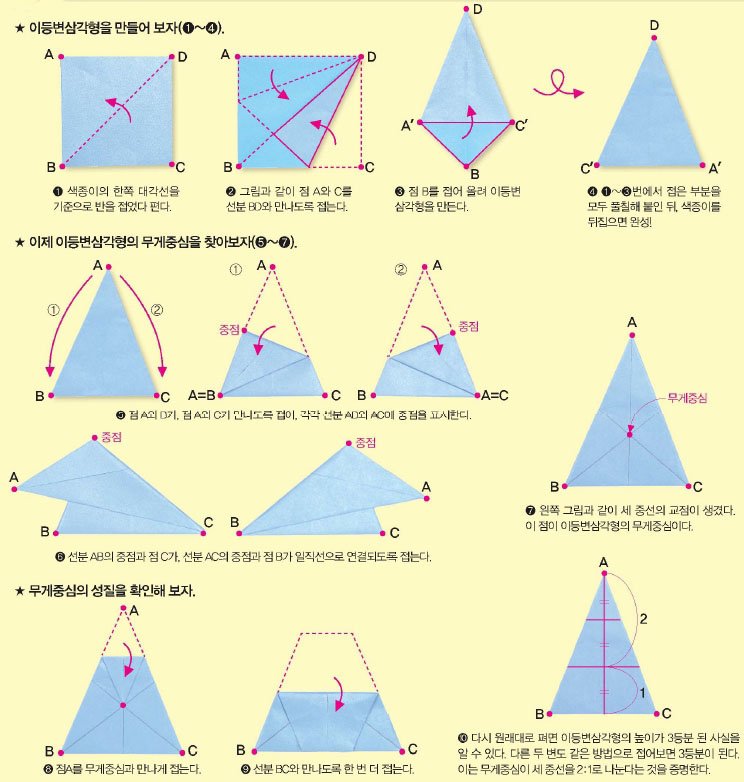
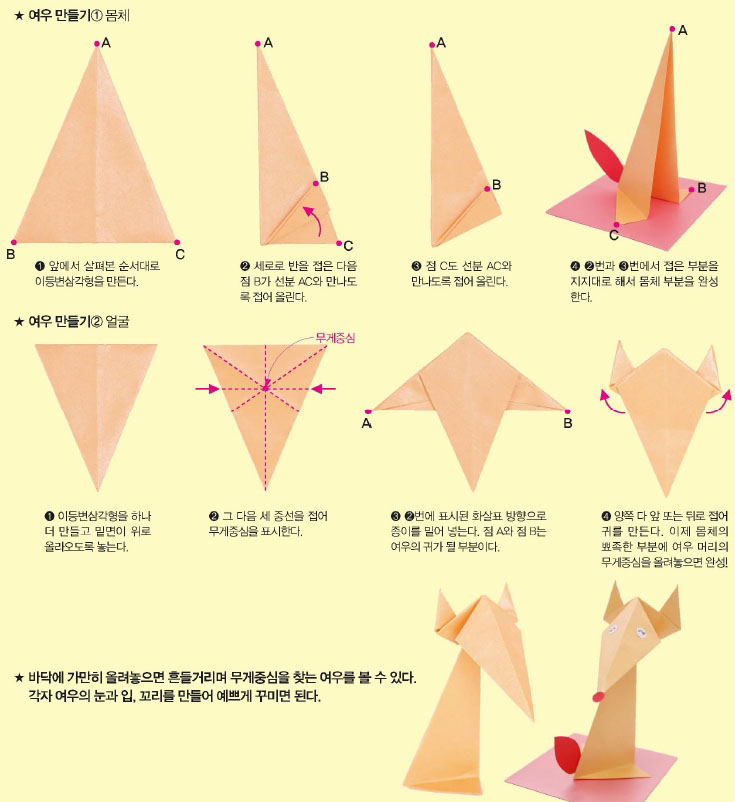
무게중심은 물체의 무게를 지탱하는 중심으로 연필, 같은 뾰족한 도구를 이용해 중심을 잡아도 균형을 잃지 않는다. 이 성질을 이용해 무게중심을 찾아 흔들리는 종이 인형을 만들어 보자.
 

*중선이란 삼각형의 각 꼭짓점과 마주보는 대변의 중심을 잇는 선분을 말한다.