d라이브러리

우리나라는 현재 올림피아드 관련 지식의 학습이 대부분 사교육에 맡겨진 상황이라서 지역에 따른 교육 기회의 차이가 심각합니다. 수학올림피아드 입상자의 9할이 수도권 학생들이고, 그중에서도 특히 강남구의 해당 지역 인구에 비례한 입상률은 전국 평균의 9배 정도입니다. 정부든 올림피아드 관련기관이든 누군가는 수학올림피아드 교과과정을 제공할 책임감을 보여야 하지 않을까 합니다. 한국에서 교육방송으로 올림피아드 공부를 할 수 있는 날이 언젠가는 오겠지요? 이번에 준비한 문제는 비교적 간단하면서도, 반짝반짝한 아이디어가 필요한 작도 문제입니다.

도시대항 국제수학토너먼트(TOT) 1987년 가을 중등부 4번

원호 AC와 꺾은선 ABC로 둘러싸인 볼록한 영역이 있다. 원호와 꺾은선은 AC에 대해 서로 반대쪽에 있다.
원호 AC의 중점을 지나 이 영역의 넓이를 이등분하는 직선을 작도하여라.

곧은 직선들로 이루어진 다각형도 아니고 곡선이 일부 포함된 도형인데 넓이를 이등분하라고 하는군요.

첫눈에는 조금 너무한다 싶은 느낌이 듭니다. 그러나, 조금만 더 생각해보면 상황이 그렇게 괴로운 것은 아님을 발견하게 될 겁니다.

원호 AC의 중점을 D라 할 때, DA, DC로 잘린 두 활꼴은 서로 합동입니다. 따라서, 이등분될 두 영역에서 이 두 활꼴을 상쇄시켜 제거하고 나면, 이 문제는 더 이상 곡선을 포함하는 문제가 아닙니다. AD = DC인볼록사각형 ABCD에서 D를 지나 이 사각형의 넓이를 이등분하는 직선을 작도하는 문제가 되지요.
 

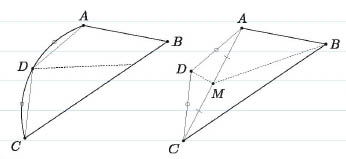
그래도 아직 쉬운 문제가 아닙니다. 이 문제는 어떻게 풀어야 할까 고민을 해봅시다.

직선 대신에 혹시 이 사각형의 넓이를 이등분하는 간단한 꺾은선을 구하라고 했다면 쉬웠을 텐데 하는 생각이 들지는 않았나요? 선분 AC의 중점을 M이라 할 때, 꺾은선 DMB가 이 사각형의 넓이를 이등분한다는 것은 쉽게 관찰이 되니까요(△ADM≡△CDM, |△ABM|=|△CBM|). 쓸모없는 생각은 그만두고 어떻게 하면 이 문제를 풀 수 있을지 생각해보자고 해야 보통이겠지만, 어떤 학생은 이게 쓸모없는 생각이 아니었다는 것을 발견할 수 있을 겁니다. 다음의 풀이를 보도록 할까요?
 

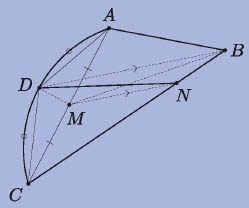
고봉균 선생님의 풀이

원호 AC의 중점을 D라 하자. 같은 넓이의 활꼴 AD와 활꼴 CD를 잘라내고 나면 □ADCB의 넓이를 이등분하는 문제가 된다. 선분 AC의 중점을 M이라 하자. 그리고, M을 지나 DB에 평행인 직선이 꺾은선 ABC와 만나는 점을 N이라 하자. N이 선분 BC 위에 있다고 해도 일반성을 잃지 않는다. 그럼 |△DMB|=|△DNB|이므로|ADNB|=|ADMB|=1/2|ABCD|이고, DN이 원하는 직선이다.

넓이를 이등분하는 꺾은선을, 등적 변형을 이용해서, 직선으로 깔끔하게 바꾸어줄 수 있었습니다. 가끔 우리 주변에서 아주 쉽게 챙길 수 있는 것들을 자르고 붙여서 다른 쓸모를 위한 물건으로 만들 수가 있는 것처럼, 가끔은 이렇게 좀 더 느슨한 조건에서의 쉬운 예를 잘 변형해서 더 까다로운 조건에서의 예로 만들 수 있을 때가 있다는 것을 기억해둡시다.