d라이브러리

우리는 인터넷을 할 때 간편한 마우스 클릭만으로 다른 웹페이지로 이동할 수 있다. 겉으로는 보이지 않지만 아마 이 연결고리를 그림으로 그리면 웹 페이지가 복잡한 그물망처럼 서로 연결되어 있을 것이다. 이런 구조를 한눈에 알아볼 수 있는 방법이 있을까? 그 방법이 바로 그래프다. 웹 페이지는 점으로, 링크되어 있는 페이지는 선으로 이으면 복잡한 구조를 보기 쉬운 그래프로 나타낼 수 있다. 이제 약 300년 전 오일러의 발상에 의해 시작된 그래프의 세계로 떠나 보자.


항공노선은 얼마나 많이 있나

우리나라는 삼면이 바다로 둘러싸여 있어 다른 나라로 갈 때 주로 비행기를 이용한다. 그런데 가려고 하는 곳마다 비행기가 모두 있을까? 항공노선은 버스노선과 달리 작은 도시까지 노선이 직접 연결되어 있지 않다. 세계에 항공노선은 얼마나 많이 있을까? 이것을 알기 위해 비행기 노선표를 보는 것은 별로 도움이 되지 않는다. 이럴 때 생각의 전환이 필요하다.

오른쪽 그림은 전 세계의 항공노선을 나타낸 것이다. 세계 각 도시에 있는 공항은 점으로, 노선은 선으로 나타냈다. 그림을 통해 선들이 밀집된 미국, 유럽, 아시아 지역은 항공노선이 많이 개설되어 있음을 알 수 있다. 그리고 대부분 작은 공항은 몇 개 주요 대도시에 연결되어 있어서 선의 개수가 적은 반면, 대도시는 수많은 항공편이 있기 때문에 선이 많아 마치 색칠된 것처럼 보인다.

이처럼 공항을 점으로 보고, 연결되는 항공노선을 선으로 보는 생각은 매우 획기적이다. 이렇게 바꿈으로써 전 세계에 얼마나 많은 노선이 개설돼 있는지, 어느 지역에 항공노선이 많은지 등을 한눈에 알 수 있다.


오일러가 뒤집은 땅과 다리

이런 생각을 처음으로 한 사람은 오일러다. 오일러가 러시아에 있을 때의 일이다. 당시 쾨니히스베르크라는 지역에는 프레겔 강이 흐르고 있었고, 이 강에는 두 개의 큰 섬이 있었다.

그리고 다리가 7개 있었는데 사람들은 7개의 다리를 한 번씩만 건너면서 처음 출발한 위치로 돌아올 수 있는지 궁금했다. 문제의 답을 찾기 위해 많은 사람들이 직접 다리를 건너며 실험했지만 길을 찾을 수 없었다. 그렇다고 그 길이 없다고 말할 근거도 찾지 못했다.

오일러는 이 문제를 어떻게 풀지 곰곰이 생각하다가 땅은 점으로, 다리는 선으로 바꿔 표현해 보았다. 이 문제를 풀기 위해 중요한 것은 다리 길이나 땅의 넓이가 아니라 다리와 땅의 연결 상태라는 걸 깨달았던 것이다. 결국 쾨니히스베르크 다리 문제는 점 4개와 선 7개가 있는 한붓그리기 문제가 되었다.
 

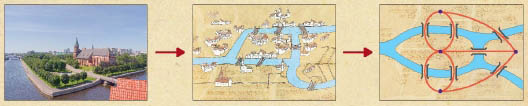
이와 같이 점과 선이 있는 그림을 그래프라고 한다. 오일러는 그래프이론이라는 수학의 새 분야의 선구자가 되었다.

이후 영국의 수학자 해밀턴은 정십이면체의 각 꼭짓점을 도시로 각 모서리를 오가는 길로 생각한 뒤, 길을 따라 도시를 단 한 번만 지나는 여행 코스가 있는지 알아 내는 문제를 냈다. 이 문제는 변을 한 번만 지나는 한붓그리기와 달리 점을 한 번씩 지나는 문제다. 해밀턴의 문제 역시 정십이면체의 20개의 꼭짓점과 30개의 모서리를 점과 선으로 바꿔 그래프로 그린 뒤 해결할 수 있다. 이처럼 점을 한 번만 지나는 문제는 여행 일정과 여비를 고려하는 여행자와 여행사가 자주 겪는다.
 

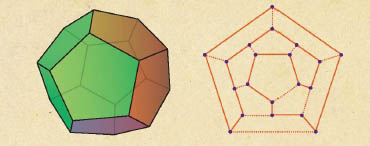
수학의 새로운 분야로 우뚝 선 그래프

이후 그래프이론은 키르히호프에 의해 전기회로를 분석할 때 쓰였다. 그리고 최초로 컴퓨터를 이용해서 증명한 사색문제는 그래프이론에 대한 관심을 불러일으켰다.

그래프이론에서 가장 중요한 것은 점과 선의, 즉 연결 상태다. 쾨니히스베르크의 지형을 그래프로 나타낼 때 직선, 곡선, 길고 짧음 등을 고려하면 여러 가지 모양으로 그릴 수 있지만, 모양과 상관 없이 모두 연결 상태가 같은 그래프가 된다.
 

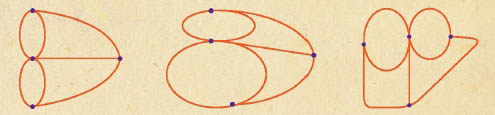
한편 오일러는 한붓그리기가 가능할 조건을 밝히고 증명했다. 어떤 점에 연결된 선의 수가 홀수일 때 그 점을 홀수점이라고 하는데, 홀수점이 없거나 2개인 그래프만 한붓그리기를 할 수 있다. 따라서 4개의 점이 모두 홀수점인 쾨니히스베르크 다리 그래프는 한붓그리기를 할 수 없다. 즉 쾨니히스베르크에서 7개의 다리를 한 번씩만 건너고 제자리로 돌아오는 것은 불가능하다.


무궁무진한 그래프의 활용

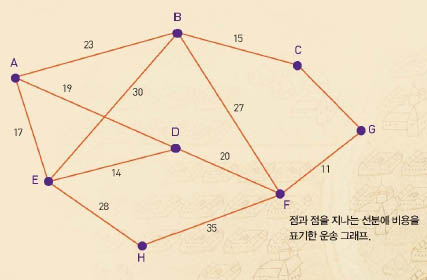
폭설이 내렸을 때 제설차는 길을 무작정 돌아다니며 눈을 치우기보다 미리 동네 길을 그래프로 나타낸 뒤, 한붓그리기를 이용해서 경로를 찾는 것이 바람직하다. 비슷한 예로 택배회사에서는 물류창고에서 택배회사 지점으로 물품을 배달할 때, 각 지점과 물류창고를 점으로, 연결도로를 선으로 나타낸 그래프를 그린다. 그 다음 가장 효율적인 경로를 찾아 물품을 분배하면 비용을 줄일 수 있다. 그래프를 그릴 때는 현실적인 방위나 거리 등은 무시하고 연결 상태만을 유지해서 그린다. 그러나 물류창고의 경우에는 제설차와 달리 각 도로의 운행거리나 통행료 등에 따라 운반비용이 달라질 수 있어 이런 정보를 그래프에 넣기도 한다.

최근 그래프이론을 응용하는 분야는 점점 더 넓어지고 있다. 택배회사는 운반비용이 적게 드는 경로를 선택할 때 그래프를 그려 생각한다. 또 의학에서도 뇌 기능을 이해하기 위해 신경세포 사이의 연결을 그래프이론으로 분석한다.신경세포의 연결 상태를 그래프이론으로 표현하면 신경망에 이상이 생겼을 때 어떤 신경세포가 망가져서 어떤 영향을 주는지 알 수 있다.

그래프이론은 다리를 건너는 문제에서 시작해 현대에는 전산망, 도로망, 인간관계, 사회조직, 생물유전자 관계 등 다양한 분야에 걸쳐 쓰이고 있다. 이처럼 수학은 복잡한 현상에서 중요한 것을 뽑아 단순화해 놀라운 결과를 이끌어 낸다. 점과 선으로 이뤄진 그래프의 눈부신 활약을 기대해 본다.
 

*사색문제 : 어떤 지도라도 4가지 색으로 이웃한 두 나라를 구분할 수 있다는 문제다.