d라이브러리

처음엔 살갑게, 배신엔 응징을, 소문은 빠르게

송준섭 기자(이하 송) : 방송 초반에는 참가자들이 서로 선택한 메뉴에 관한 정보를 교환하는 데 초점을 맞췄는데, 돌연 한 플레이어가 모두 같은 메뉴를 고르고 11을 예측하자고 제안했다. 최대한 승점을 많이 벌어서 상금을 많이 획득하자는 전략이었다. 누군가의 배신으로 결국엔 실패로 끝나긴 했지만 아이디어가 흥미로웠다.

김영진 석박사 통합과정(이하 김) : 제안대로 모두가 짜장면을 선택할 때 출연자 전체의 효용이 가장 크다. 마치 죄수의 딜레마에 빠진 죄수들이 서로를 믿고 배신하지 않을 때처럼 말이다. 하지만 한명이라도 배신을 하고 다른 메뉴를 선택하면, 짬뽕을 선택한 개인의 효용은 협동했을 때보다 커진다. 비록 전체의 이익은 떨어지지만 말이다.

정선영 석사 과정(이하 선) : 전체를 위해서는 협동하는 게 좋지만 나를 위해서는 무조건 배신하는 게 좋다는 말로 들린다. 그렇다면 죄수의 딜레마에 빠진 11인의 협동은 정녕 불가능한가.

손승우 교수(이하 손) : 꼭 그렇지만은 않다. 미국 하버드대 마틴 노왁 교수가 2006년 ‘사이언스’에 죄수의 딜레마에 빠진 사람들이 협동하는 과정을 수학적으로 설명했다.

송 : 협동을 수학적으로 어떻게 정의할 수 있나.

정현우 석사 과정(이하 현) : 간단하다. 협동을 선택했을 때 얻는 이익을 b, 협동 시 포기하는 기회비용을c라고 해보자. 그렇다면 협동을 했을 때 내가 얻을 수 있는 순이익은 b-c다.

손 : 노왁은 이를 바탕으로 협동을 크게 몇 가지로 나눴는데, 그중 첫 번째는 친족 선택이다. 가족, 친지같은 가까운 사람의 유전적 연관도 r이 c/b보다 클 때 상대를 믿고 협동한다는 것이다. 두 번째 종류는 응징에 의한 협동이다. 죄수의 딜레마 게임을 반복하면 어떻게 될까. 처음에는 배신과 반복 사이에서 갈피를 잡지 못하던 참가자들이 시간이 지나면 상대를 믿고 협동한다. 이번 게임에 상대가 나를 배신하면 다음에는 배신으로 보복하면 된다는 것을 깨달은 것이다. 대신에 이럴 경우에는 반드시 다음에 똑같은 게임을 한다는 보장이 있어야 한다. 노왁의 표현을 빌리면, 다음 라운드가 열릴 확률을 w라고 하면 w가 c/b보다 커야 이런 종류의 협동이 생길 수 있다. 출연자들이 협동을 꾀한 뒤 배신을 철저히 응징했다면 11인이 협동할 수도 있었을 것이다.
 

김 : 이렇게 직접적으로 협동과 응징을 주고받는 것외에도 나의 평판을 끌어올리는 것으로 신뢰를 얻을수도 있다. 이것을 ‘간접적 호혜’라고 한다. 간접적 호혜는 ‘내가 누군가를 도와줬으니 언젠가 다른 사람이 나를 도와줄 것이다’라는 기대에서 출발한다. 이 사람은 믿을만하다는 평판이 있으면 그 사람에게 도움을 받은 적이 없다고 하더라도 협동할 수 있다. 상대가 평판을 들었을 확률을 q라고 하면 q가  c/b보다 클 때 간접적 호혜가 생긴다. 지니어스는 참가자가 10명 내외로 작기 때문에 q 값이 꽤 클 것이다. 간접적 호혜를 구축하는 게 그리 어렵지 않을 것이다.

송 : 이번 기사로 내 평판이 올라가서 다음 달에는 더 많은 과학자와 생존법을 이야기했으면 좋겠다. 어서 빨리 SNS에 오늘 일을 올려 다른 과학자들에게도 이 사실을 알려 달라.

]

생존법1. 분배의 문제, 준결승의 역설

송 : 자신이 이길 때는 작은 차이로 이기고, 질 때는 큰 차이로 지는 게 방송에서 나온 해법이다. 내가 이길 때는 흰색 1로 검은색 0을 이기고, 질 때는 상대의 8에 0으로 지는 게 유리하다는 것이다.

손 : 게임이론으로도 증명된 전략이다. 올해 초에 ‘피지컬 리뷰 E’에 내가 발표한 논문을 예로 들어보겠다. 월드컵 4강에 오른 팀의 감독이라고 가정하자. 준결승에 오를 정도면 상대도 거의 대등한 실력이고, 이미 이전 경기에서 비슷한 체력을 소모했다. 우승을 위해서는 앞으로 경기를 두 번 치러야 하는데, 4강에서 너무 힘을 쏟으면 되레 결승에서 맥없이 질 수도 있다. 이것을 준결승의 딜레마라고 부른다. 팀의 체력이 100이라면 어떻게 분배하는 게 좋을까.

송 : 당장 눈앞의 경기를 이기지 못하면 말짱 도루묵 아닌가. 나라면 준결승에 80, 결승에 20을 쓰겠다.

손 : 일리는 있지만 게임이론으로 만든 최적의 전략은 이렇다. 월드컵처럼 승자가 모든 영광을 차지하는 게임이라면 준결승에서 상대편이 경기 중에 사용하는 것보다 아주 조금 더 쓰면 된다. 상대가 40을 쓴다면 41을 쓰는 것이 우승할 확률이 가장 높았다. 흑과 백 게임과 비슷한 전략이다.

현 : 상대가 얼마만큼의 힘으로 경기에 임하는지를 파악하는 게 가장 중요하다. 그러면서 나는 상대에게 정보를 숨겨야 한다. 흑과 백 게임을 할 때 출연진이 서로 대화할 수 있게 허용해준 것을 보면 이런 정보싸움을 적극적으로 권장하는 것 같다.

김 : 그래서 선공으로 1라운드를 시작할 때는 검은색 패를 내는 게 낫다. 검은색 패는 다섯 개인 반면, 흰색은 네 개뿐이기 때문에 검은색을 내면 상대에게 조금이라도 정보를 적게 준다. 게임 초반에 작은 숫자를 내는 것도 좋은 방법이다. 게임을 시작할 때는 상대가 6,7,8 같은 높은 숫자를 가지고 있는 게 확실하다. 확실한 정보가 있을 때 작은 숫자를 내서 차이를 벌리는 게 좋다. 나라면 첫 라운드 때 검은색 0을 내겠다.

 생존법2. 당신 마음의 깊이
 
선 : 만약 상대도 똑같은 전략을 구사하면 어떻게 될까. 그렇다면 내가 0을 낸 것을 알고 1을 내지 않을까.

송 : 그러면 2를 내면 된다. 설마 이것까지 생각하고 3을 내지는 않겠지.

김 : 이렇게 A라는 전략을 B가 이기고, B를 C가 이기고, C가 다시 다른 전략에게 먹히는 상황에서는 새로운 전략이 필요하다. 

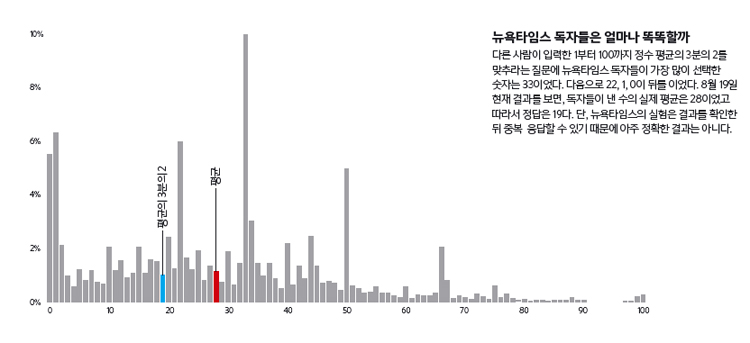
손 : 그래서 게임이론을 연구하는 사람들은 최근에는 ‘마음의 깊이’를 연구한다. 마음의 깊이란 사람들이 몇 번이나 상대의 수를 읽으려고 시도하는지를 나타내는 것이다. 예를 들어 1부터 100까지의 정수 중 하나를 고르는 게임이 있다. 그런데 조건이 하나 있다. 주최 측에서 사람들이 고른 숫자 평균의 3분의 2에 가장 근접한 값을 고른 사람에게 상금을 주기로 한것이다. 조건이 없이 충분한 수의 사람이 투표에 참여한다면 평균은 결국 50에 수렴할 것이다. 이것을 근거로 50의 3분의 2인 33을 선택해야 할까. 아니면 33까지는 다른 사람이 생각을 할 테니, 33의 3분의 2인 22를 선택하는 게 맞을까.

선 : 그런 식이면 결국엔 무한히 숫자가 작아져 0을 선택해야 될 것 같다.

손 : 모든 사람이 완벽히 합리적이라면 그렇지만 실제 결과는 조금 다르다(실험실 프로젝터를 부랴부랴 켠다). 뉴욕타임스가 지난 8월 13일 게시한 글이다. ‘당신은 뉴욕타임스의 다른 5만5064명의 독자보다 똑똑한가요?’라는 도발적인 제목이 붙었다. 위에서 설명한 것과 똑같은 실험을 온라인으로 했다. 실험결과 뉴욕타임스 독자들이 가장 많이 선택한 숫자는 10%가 선택한 33이었다. 그 다음으로 5~6%가량이 선택한 22, 0, 1이 뒤를 이었다. 이 실험에 따르면 사람의 마음 깊이는 대개 한 번 또는 두 번인 셈이다.

송 : 결론은 검은색 0을 낸 다음 한 번 또는 두 번 정도 상대의 수를 읽어서 2 또는 3을 내라는 건가.

손 : 꼭 그렇지만은 않다. 프로그램에 사용되는 게임 대부분이 이런 식으로 꼬리에 꼬리를 물며 상대의 수를 읽어야 하는 게임이다. 그렇기에 어떤 규칙을 단정 짓기보다는 상대방으로부터 끊임없이 정보를 수집해 선택을 하는 게 더 효과적이다.