공부의 주체는 학생이며 스스로 질문하고 답변할 때 진정한 공부가 이뤄진다고 믿는다.
학생들이 이런 능력을 갖출 때까지 끊임없이 자극하고 격려하는 사람이 되기 위해 노력하고 있다.
음악은 인류의 역사만큼이나 오래됐다. 고대 문명에서 음악은 집단적인 제사나 축제에서 공동체를 이어주고, 싸움에서 전사들에게 용기를 주는 중요한 역할을 했다. 거의 모든 인류 문명과 집단은 음악에 관심이 있었다. 그들은 소리를 만들기 위한 목적으로 여러 가지 ‘악기’를 발달시켰다. 악기가 만들어내는 소리는 같은 악보를 연주하더라도 악기의 종류에 따라 매우 다르다. 소리는 과학적 입장에서 보면 파동을 의미한다. 악기가 소리를 만들어내는 방법과 저마다 다른 소리가 나는 이유를 고교과정의 공통과학과 물리I의 ‘파동’을 바탕으로 설명해보자.
※다음 제시문을 읽고 물음에 답하라.
(가) 가야금이나 기타 같은 현악기는 일정한 길이의 줄이 떨릴 때 규칙적인 진동을 갖는 정상파를 만든다. 정상파는 진동수가 같고 진동 방향이 반대인 두 파동이 서로 반대방향으로 진행하며 중첩됐을 때 나타난다. 이때 줄이 만드는 파동은 진폭이 작아 소리가 작기 때문에 현악기는 울림통에서 같은 진동수를 갖는 파동을 겹쳐 진폭을 키워 소리를 크게 만든다.
대금이 소리를 내는 원리도 현악기와 같다. 대금은 내부를 이동하는 공기의 기둥인 ‘기주’가 진동하며 소리를 낸다. 일종의 ‘보이지 않는 줄’로 소리를 내는 셈이다. 대금에 바람을 불어 넣으면 내부 공기에 진동이 일어나 정상파를 만들고, 대금의 관 자체가 울림통 역할을 한다. 관에 생긴 정상파의 진동수가 기주의 고유진동수와 일치하면 공명이 일어나 소리가 커진다. 대금은 지공이 6개뿐이지만 가장 낮은 옥타브인 ‘저취’(약 230~430Hz), 중간 대역인 ‘평취’(약 470~860Hz), 가장 높은 ‘역취’(약 970~1520Hz)까지 3옥타브를 넘나들며 24개 이상의 음을 낸다. 음높이는 진동수에 따라 결정되는데 진동수가 높으면 높은음이 되고 진동수가 낮으면 낮은음이 된다. 대금에서 음을 높이는 방법은 두 가지다. 손가락으로 막았던 지공을 하나씩 떼거나 대금을 세게 부는 것이다.
지공을 여닫을 때 음높이가 변하는 이유는 뭘까. 물체 길이에 따라 고유진동수가 달라지기 때문이다. 고유진동수는 파장이 짧을수록 크다. 손가락으로 지공을 완전히 다 막으면 바람이 빠져나가지 못해 고유진동수가 작아진다. 지공을 열면 그만큼 악기 길이가 짧아지는 효과가 나타나 고유진동수는 커진다. 바람을 세게 불어넣을 때도 한 옥타브 높은 음을 낼 수 있다. 바람을 세게 불어 공기가 빠르게 움직이면 단위 시간당 진동수가 커진다. 테이프에 목소리를 녹음한 뒤 2배속으로 재생하면 진동수가 커져 목소리가 한 옥타브 높게 들리는 것과 같은 원리다.

- 과학동아 2008년 12월호 ‘천상의 소리 대금’
(나) 음정은 동시에 울리거나 연이어 울리는 두 음 높이의 간격이다. 일반적으로 ‘도’를 단위로 해서 음계에서 똑같은 단계에 있는 두 음의 음정을 1도, 한 단계 떨어져 있는 두 음의 음정을 2도라 한다. 간격이 한 단계씩 넓어짐에 따라 3도, 4도라 하고, 8도를 1옥타브라고 부른다. 피타고라스는 장력과 재질이 서로 같은 두 현을 퉁겼을 때 나오는 두 음이 길이 비가 2:1이면 8도, 3:2이면 5도, 4:3이면 4도 음정이 난다는 사실을 발견했다. 현의 길이가 간단한 정수 비로 표현될수록 어울리는 소리가 나고, 복잡할수록 어울리지 않는다는 사실도 발견했다. 실제로 1도, 4도, 5도, 8도 음정을 완전 어울림 음정이라고 한다. 피타고라스의 음정 이론은 서양 음악 이론의 출발점이 되면서 음악과 수학은 밀접한 관계를 맺었다.
- 과학동아 1999년 10월호 ‘피타고라스의 음정 이론’
(다) 기타와 같은 현악기의 현을 튀기면 진행파와 반사파가 서로 중첩되어 항상 진동하는 부분과 전혀 진동하지 않는 부분이 생긴다. 이렇게 만들어진 파동은 마치 어느 방향으로도 진행하지 않는 것처럼 보이는 정상파이다. 일반적인 파동은 매질의 모든 부분이 진동하지만 정상파는 매질이 많이 진동하는 곳, 조금 진동하는 곳, 전혀 진동하지 않는 곳이 있다.
정상파에서 진폭이 가장 큰 곳을 배라 하고 진동이 전혀 일어나지 않는 곳을 마디라고 한다. 줄의 양 끝을 고정시키고 중간점을 손가락으로 튀기면 줄 전체가 하나의 구간을 이루는 정상파가 생긴다. 이때의 진동은 파장이 가장 길고 진동수가 가장 작으므로 기본 진동이다. 기본 진동을 하는 줄 길이의 1/2, 1/3,… 되는 곳을 살짝 누르면 2개의 구간, 3개의 구간, …으로 나눠져 진동하는 정상파가 된다. 이러한 진동을 2배 진동, 3배 진동, …이라고 한다.
- 2008학년도 건국대 정시 제시문 발췌
(라) 모든 파동은 매질의 한 점이 한 번 진동하는 동안에 한 파장의 거리를 진행해 간다. 매질이 한 번 진동하는데 걸리는 시간이 주기이므로 파동이 1초 동안에 진행하는 거리 즉 파동의 속력은 이동거리인 파장을 걸린 시간인 주기로 나누면 구할 수 있다. 파동의 파장을 λ, 주기를 T, 진동수를 f로 나타내면 파동의 속력 v는 v=λ/T=fλ과 같이 나타낸다.
- 고등학교 물리I 교과서
1-1) 건반 악기에는 1옥타브를 반음씩 12등분한 평균율(equal temperament)이 일반적으로 쓰인다. 반음씩 등분한다는 것은 각 음에 대응하는 진동수 비를 일정하게 정한다는 뜻이다. 피아노는 현을 망치로 때려 소리를 내는 구조다. 제시문을 바탕으로 진동수 비를 구하라.
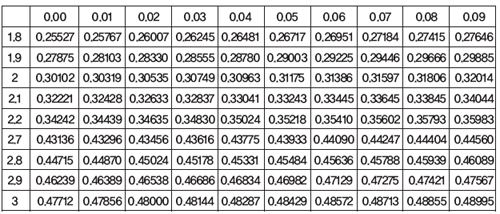
1-2) 앞의 논제를 바탕으로 처음 친 건반이 C음(264Hz)을 냈을 때 처음 친 건반보다 현의 길이가 2/3인 건반이 내는 음은 어떤 음일지 다음 로그표를 이용해 설명하라.
전문가 클리닉
현의 길이와 악기 소리의 진동수 간 관계를 이해하는 것이 문제 해결의 시작입니다. 문제에서 요구하는 값을 얻기 위해서는 고교과정의 수열에 대한 이해가 필요합니다. 이런 배경지식을 바탕으로 논제에서 주어진 ‘반음이 증가할 때마다 증가하는 진동수 비가 일정하다’는 말의 의미를 파악해 반음씩 증가하는 횟수와 진동수의 관계를 양적으로 표현할 수 있어야 합니다.
예시답안
1-1) 현이 만들어내는 소리의 진동수(f)는 v=λ /T =fλ, f=v/λ다. 이때 만들어지는 정상파의 파장은 현의 길이의 2배이므로 길이 l인 현이 만들어내는 소리의 진동수는 f=v/2l이다. 1옥타브란 기준이 되는 한 음과 8도 떨어져 있는 음 사이의 음정(음 사이의 거리)이고, 1옥타브 차이는 현의 길이 비가 2:1일 때 나타난다. 현이 만들어내는 소리의 진동수는 다음과 같다.
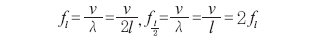
1옥타브를 12등분했을 때 각 진동수 비는 일정하므로
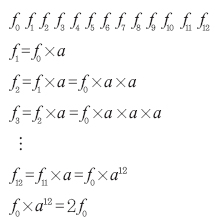
그러므로 반음이 높아질 때마다 진동수는 a=12√2=1.05946배가 된다.

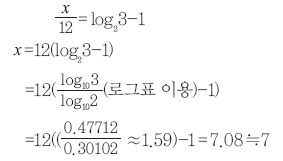
두 음은 반음의 7배 즉 3.5음 차이가 난다. 평균율을 바탕으로 만든 서양 음간의 음의 차이는 ‘C-한음차이-D-한음차이-E-반음 차이-F-한 음 차이-G-한 음 차이-A-한 음 차이-B-반음 차이-C’이다. 결국 C로부터 3.5음 차이나는 음은 G가 된다.
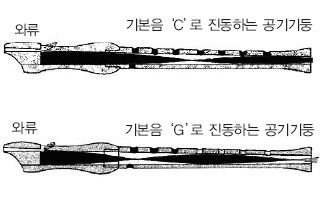
2. 제시문 (가)의 밑줄 친 내용을 바탕으로 개관악기인 리코더가 그림과 같이 두 가지 운지 상태일 때 내부 음파의 모습을 예상하라.

전문가 클리닉
정상파의 모양을 결정하는 요소는 배와 마디의 위치입니다. 현의 경우 현이 묶여 있는 양쪽 끝은 진동할 수 없기 때문에 결국 양쪽 끝이 마디가 돼 정상파를 형성합니다. 그에 반해 관의 경우는 관의 형태에 따라 모양이 다른 정상파가 생깁니다. 한 쪽이 막힌 폐관의 경우 막혀 있는 끝의 공기는 진동할 수 없으므로 마디가 되고 막혀 있지 않은 반대쪽은 배가 됩니다. 양쪽 모두 열려 있는 개관의 경우에는 관의 양쪽 끝이 배가 되고 내부에 마디가 생깁니다. 이처럼 제시문에 나온 정상파에 대한 이해를 바탕으로 현이 아닌 관속에서 발생하는 정상파의 모양을 예측할 수 있어야 합니다.
예시답안
관악기 역시 현악기와 동일하게 정현파를 형성해 소리를 만들어낸다. 관악기의 경우 관의 모양에 따라 정현파의 모양이 달라진다. 관의 한쪽 끝이 막혀 있는 경우를 폐관이라고 하고, 양쪽 모두 열려 있는 경우를 개관이라고 한다. 개관에서 형성되는 정상파의 모양은 다음 그림과 같다.
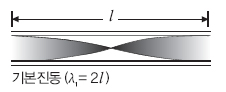
리코더는 개관이다. 구멍을 모두 막은 A의 경우 바람을 불어넣는 부분과 관의 끝 부분만 공기가 자유롭게 진동할 수 있으므로 양쪽 끝이 배가 돼 다음 그림과 같은 정상파를 형성한다.
구멍을 모두 막지 않은 B의 경우 열려있는 구멍을 통해 공기가 자유롭게 진동할 수 있으므로 구멍 부분이 배가 돼 그림과 같은 정상파를 형성한다.
학생들이 이런 능력을 갖출 때까지 끊임없이 자극하고 격려하는 사람이 되기 위해 노력하고 있다.
음악은 인류의 역사만큼이나 오래됐다. 고대 문명에서 음악은 집단적인 제사나 축제에서 공동체를 이어주고, 싸움에서 전사들에게 용기를 주는 중요한 역할을 했다. 거의 모든 인류 문명과 집단은 음악에 관심이 있었다. 그들은 소리를 만들기 위한 목적으로 여러 가지 ‘악기’를 발달시켰다. 악기가 만들어내는 소리는 같은 악보를 연주하더라도 악기의 종류에 따라 매우 다르다. 소리는 과학적 입장에서 보면 파동을 의미한다. 악기가 소리를 만들어내는 방법과 저마다 다른 소리가 나는 이유를 고교과정의 공통과학과 물리I의 ‘파동’을 바탕으로 설명해보자.
※다음 제시문을 읽고 물음에 답하라.
(가) 가야금이나 기타 같은 현악기는 일정한 길이의 줄이 떨릴 때 규칙적인 진동을 갖는 정상파를 만든다. 정상파는 진동수가 같고 진동 방향이 반대인 두 파동이 서로 반대방향으로 진행하며 중첩됐을 때 나타난다. 이때 줄이 만드는 파동은 진폭이 작아 소리가 작기 때문에 현악기는 울림통에서 같은 진동수를 갖는 파동을 겹쳐 진폭을 키워 소리를 크게 만든다.
대금이 소리를 내는 원리도 현악기와 같다. 대금은 내부를 이동하는 공기의 기둥인 ‘기주’가 진동하며 소리를 낸다. 일종의 ‘보이지 않는 줄’로 소리를 내는 셈이다. 대금에 바람을 불어 넣으면 내부 공기에 진동이 일어나 정상파를 만들고, 대금의 관 자체가 울림통 역할을 한다. 관에 생긴 정상파의 진동수가 기주의 고유진동수와 일치하면 공명이 일어나 소리가 커진다. 대금은 지공이 6개뿐이지만 가장 낮은 옥타브인 ‘저취’(약 230~430Hz), 중간 대역인 ‘평취’(약 470~860Hz), 가장 높은 ‘역취’(약 970~1520Hz)까지 3옥타브를 넘나들며 24개 이상의 음을 낸다. 음높이는 진동수에 따라 결정되는데 진동수가 높으면 높은음이 되고 진동수가 낮으면 낮은음이 된다. 대금에서 음을 높이는 방법은 두 가지다. 손가락으로 막았던 지공을 하나씩 떼거나 대금을 세게 부는 것이다.
지공을 여닫을 때 음높이가 변하는 이유는 뭘까. 물체 길이에 따라 고유진동수가 달라지기 때문이다. 고유진동수는 파장이 짧을수록 크다. 손가락으로 지공을 완전히 다 막으면 바람이 빠져나가지 못해 고유진동수가 작아진다. 지공을 열면 그만큼 악기 길이가 짧아지는 효과가 나타나 고유진동수는 커진다. 바람을 세게 불어넣을 때도 한 옥타브 높은 음을 낼 수 있다. 바람을 세게 불어 공기가 빠르게 움직이면 단위 시간당 진동수가 커진다. 테이프에 목소리를 녹음한 뒤 2배속으로 재생하면 진동수가 커져 목소리가 한 옥타브 높게 들리는 것과 같은 원리다.

- 과학동아 2008년 12월호 ‘천상의 소리 대금’
(나) 음정은 동시에 울리거나 연이어 울리는 두 음 높이의 간격이다. 일반적으로 ‘도’를 단위로 해서 음계에서 똑같은 단계에 있는 두 음의 음정을 1도, 한 단계 떨어져 있는 두 음의 음정을 2도라 한다. 간격이 한 단계씩 넓어짐에 따라 3도, 4도라 하고, 8도를 1옥타브라고 부른다. 피타고라스는 장력과 재질이 서로 같은 두 현을 퉁겼을 때 나오는 두 음이 길이 비가 2:1이면 8도, 3:2이면 5도, 4:3이면 4도 음정이 난다는 사실을 발견했다. 현의 길이가 간단한 정수 비로 표현될수록 어울리는 소리가 나고, 복잡할수록 어울리지 않는다는 사실도 발견했다. 실제로 1도, 4도, 5도, 8도 음정을 완전 어울림 음정이라고 한다. 피타고라스의 음정 이론은 서양 음악 이론의 출발점이 되면서 음악과 수학은 밀접한 관계를 맺었다.
- 과학동아 1999년 10월호 ‘피타고라스의 음정 이론’
(다) 기타와 같은 현악기의 현을 튀기면 진행파와 반사파가 서로 중첩되어 항상 진동하는 부분과 전혀 진동하지 않는 부분이 생긴다. 이렇게 만들어진 파동은 마치 어느 방향으로도 진행하지 않는 것처럼 보이는 정상파이다. 일반적인 파동은 매질의 모든 부분이 진동하지만 정상파는 매질이 많이 진동하는 곳, 조금 진동하는 곳, 전혀 진동하지 않는 곳이 있다.
정상파에서 진폭이 가장 큰 곳을 배라 하고 진동이 전혀 일어나지 않는 곳을 마디라고 한다. 줄의 양 끝을 고정시키고 중간점을 손가락으로 튀기면 줄 전체가 하나의 구간을 이루는 정상파가 생긴다. 이때의 진동은 파장이 가장 길고 진동수가 가장 작으므로 기본 진동이다. 기본 진동을 하는 줄 길이의 1/2, 1/3,… 되는 곳을 살짝 누르면 2개의 구간, 3개의 구간, …으로 나눠져 진동하는 정상파가 된다. 이러한 진동을 2배 진동, 3배 진동, …이라고 한다.
- 2008학년도 건국대 정시 제시문 발췌
(라) 모든 파동은 매질의 한 점이 한 번 진동하는 동안에 한 파장의 거리를 진행해 간다. 매질이 한 번 진동하는데 걸리는 시간이 주기이므로 파동이 1초 동안에 진행하는 거리 즉 파동의 속력은 이동거리인 파장을 걸린 시간인 주기로 나누면 구할 수 있다. 파동의 파장을 λ, 주기를 T, 진동수를 f로 나타내면 파동의 속력 v는 v=λ/T=fλ과 같이 나타낸다.
- 고등학교 물리I 교과서
1-1) 건반 악기에는 1옥타브를 반음씩 12등분한 평균율(equal temperament)이 일반적으로 쓰인다. 반음씩 등분한다는 것은 각 음에 대응하는 진동수 비를 일정하게 정한다는 뜻이다. 피아노는 현을 망치로 때려 소리를 내는 구조다. 제시문을 바탕으로 진동수 비를 구하라.
1-2) 앞의 논제를 바탕으로 처음 친 건반이 C음(264Hz)을 냈을 때 처음 친 건반보다 현의 길이가 2/3인 건반이 내는 음은 어떤 음일지 다음 로그표를 이용해 설명하라.

전문가 클리닉
현의 길이와 악기 소리의 진동수 간 관계를 이해하는 것이 문제 해결의 시작입니다. 문제에서 요구하는 값을 얻기 위해서는 고교과정의 수열에 대한 이해가 필요합니다. 이런 배경지식을 바탕으로 논제에서 주어진 ‘반음이 증가할 때마다 증가하는 진동수 비가 일정하다’는 말의 의미를 파악해 반음씩 증가하는 횟수와 진동수의 관계를 양적으로 표현할 수 있어야 합니다.
예시답안
1-1) 현이 만들어내는 소리의 진동수(f)는 v=λ /T =fλ, f=v/λ다. 이때 만들어지는 정상파의 파장은 현의 길이의 2배이므로 길이 l인 현이 만들어내는 소리의 진동수는 f=v/2l이다. 1옥타브란 기준이 되는 한 음과 8도 떨어져 있는 음 사이의 음정(음 사이의 거리)이고, 1옥타브 차이는 현의 길이 비가 2:1일 때 나타난다. 현이 만들어내는 소리의 진동수는 다음과 같다.
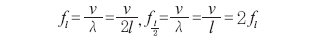
1옥타브를 12등분했을 때 각 진동수 비는 일정하므로
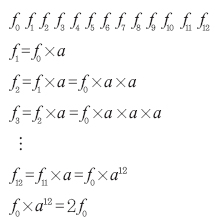
그러므로 반음이 높아질 때마다 진동수는 a=12√2=1.05946배가 된다.

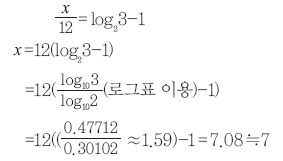
두 음은 반음의 7배 즉 3.5음 차이가 난다. 평균율을 바탕으로 만든 서양 음간의 음의 차이는 ‘C-한음차이-D-한음차이-E-반음 차이-F-한 음 차이-G-한 음 차이-A-한 음 차이-B-반음 차이-C’이다. 결국 C로부터 3.5음 차이나는 음은 G가 된다.
2. 제시문 (가)의 밑줄 친 내용을 바탕으로 개관악기인 리코더가 그림과 같이 두 가지 운지 상태일 때 내부 음파의 모습을 예상하라.

전문가 클리닉
정상파의 모양을 결정하는 요소는 배와 마디의 위치입니다. 현의 경우 현이 묶여 있는 양쪽 끝은 진동할 수 없기 때문에 결국 양쪽 끝이 마디가 돼 정상파를 형성합니다. 그에 반해 관의 경우는 관의 형태에 따라 모양이 다른 정상파가 생깁니다. 한 쪽이 막힌 폐관의 경우 막혀 있는 끝의 공기는 진동할 수 없으므로 마디가 되고 막혀 있지 않은 반대쪽은 배가 됩니다. 양쪽 모두 열려 있는 개관의 경우에는 관의 양쪽 끝이 배가 되고 내부에 마디가 생깁니다. 이처럼 제시문에 나온 정상파에 대한 이해를 바탕으로 현이 아닌 관속에서 발생하는 정상파의 모양을 예측할 수 있어야 합니다.
예시답안
관악기 역시 현악기와 동일하게 정현파를 형성해 소리를 만들어낸다. 관악기의 경우 관의 모양에 따라 정현파의 모양이 달라진다. 관의 한쪽 끝이 막혀 있는 경우를 폐관이라고 하고, 양쪽 모두 열려 있는 경우를 개관이라고 한다. 개관에서 형성되는 정상파의 모양은 다음 그림과 같다.

리코더는 개관이다. 구멍을 모두 막은 A의 경우 바람을 불어넣는 부분과 관의 끝 부분만 공기가 자유롭게 진동할 수 있으므로 양쪽 끝이 배가 돼 다음 그림과 같은 정상파를 형성한다.
구멍을 모두 막지 않은 B의 경우 열려있는 구멍을 통해 공기가 자유롭게 진동할 수 있으므로 구멍 부분이 배가 돼 그림과 같은 정상파를 형성한다.