'우주는 무한한가 유한한가' 이 명제는 우주가 영원히 팽창할 것인가, 아니면 어느 순간에 다시 수축해 무한 밀도의 한점이 될 것인가라는 문제와 관련돼 있다.
외부 은하들이 그 거리에 비례하는 속도로 멀어져 가고 있다는 에드윈 허블의 발견은 천체들의 분포에 관한 인간의 지식을 크게 넓히게 된 동기가 됐다. 우주가 팽창하고 있다는 이 발견의 의미는 과거로 갈수록 우주는 점점 작았으며 모든 물질과 빛은 결국 무한대의 밀도를 가진 점에서 출발했다는 것이다.
이것이 약 1백50억년 전에 있었다고 추정되는 빅뱅이다. 1965년 전파 천문학자인 펜지아스와 윌슨은 바로 이 빅뱅으로부터 남겨진 빛인 우주여광(우주배경복사)을 발견함으로써 이 이론을 입증했다. 정확히 빅뱅이 어떻게 시작했으며, 어떻게 그 이후 우주의 진화에 영향을 미쳤으며, 우주의 미래에 대해 어떤 운명을 가르쳐 주는가 하는 질문은 우주론을 연구하는 과학자들뿐만 아니라, 모든 현대인의 관심사일 것이다.
시공의 구조를 이해해야
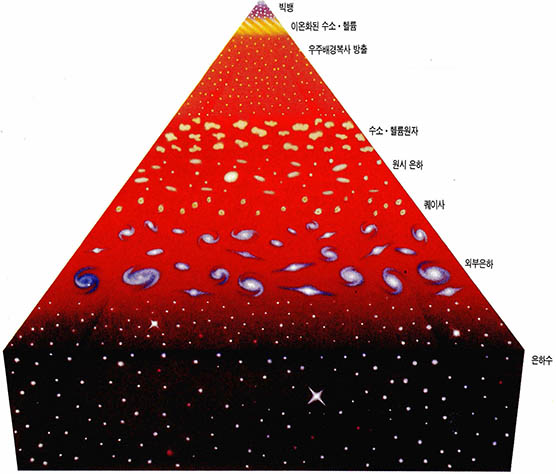
먼저 유의해야 할 점은 우주의 구조라는 명제가 그 공간적인 구조만을 의미하지 않는다는 것이다. 우주의 구조는 시공의 세계에서 이해되어야 한다. 그래서 천문학자들은 공간적으로 가능한 한 멀리까지 관측하려 한다. 이는 곧 우주의 과거에서의 상태를 보고자 하는 것과 같다. 밤하늘에 반짝이는 별빛과 은하들은 오랜 옛날에 출발한 빛이고, 지금 '이 순간의 우주'는 우리가 사는 평생동안 아주 조금 밖에 볼 수 없다(그림 2).
우주의 구조를 이해하기 위해 반드시 알아야 할 또 한가지 사실이 있다. 보통 공간이라고 하면, 우리는 아무것도 있는 팅빈 어떤 것을 연상하고 두점의 거리를 잴 때 그 사이에 있는 것이라고 말한다. 따라서 물질은 그런 공간에 담기는 것이고, 공간과 물질 사이에는 아무런 관계가 없다고 믿고 있다.
일반상대성이론에 따르면 이 두 개념 사이에는 밀접한 관계가 있다. 물질의 양과 분포가 곧 공간의 구조를 결정해 주고, 물질의 운동은 공간의 구조에 의해 영향을 받는다는 것이다. 그래서 우주의 구조라는 운명을 결정해주는 중요한 요소는 우주안에 얼마나 많은 물질이 있는가 하는 것이다.

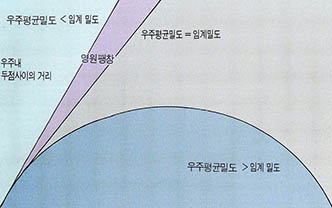
만약 우주안에 물질이 평균적으로 1㎥속에 수소원자 세개의 질량(이를 임계밀도라 한다)보다 많으면, 우주의 공간은 유한하다(닫힌 우주). 즉 우주의 부피를 이야기할 수 있다. 또 이 경우 미래의 우주는 현재의 팽창을 결국 이겨내고 다시 수축을 해 모두 무한대의 밀도인 뜨거운 한 점으로 떨어져 들어갈 것이다. 만약 우주의 평균밀도가 이 임계밀도보다 같거나 작으면 우주의 공간은 무한하다(열린 우주). 열린 우주는 끝이 있으며 무한대의 부피를 갖는다. 이런 경우 우주는 영원히 팽창해 밤하늘에 떠있는 거의 모든 외부은하들이 보이지 않게 될 것이다.
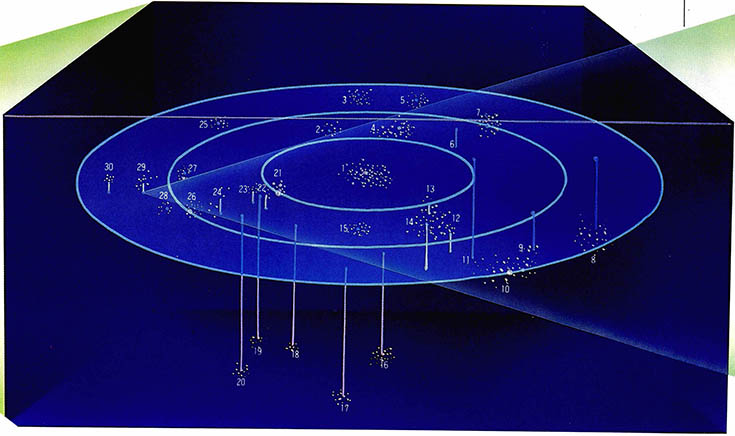
우주는 유한한가 무한한가. 위에서 설명한 바와 같이 이 질문의 해답은 우주의 평균 밀도를 재면 구할 수 있다. 불행히도 현재의 관측값은 임계 밀도의 10분의 1에서 임계 밀도의 두배 사이라는 구간에 있다. 따라서 우주는 닫혀있을 수도 열려 있을 수도 있다(그림5).
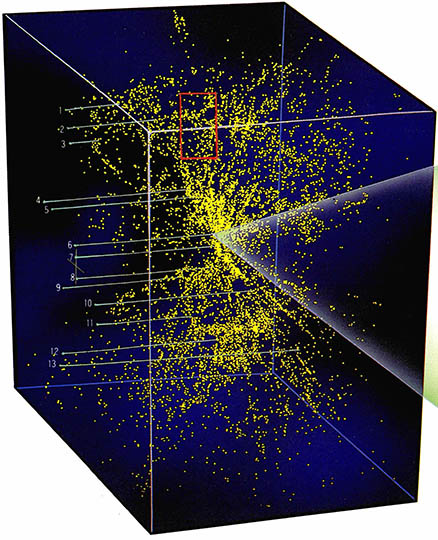
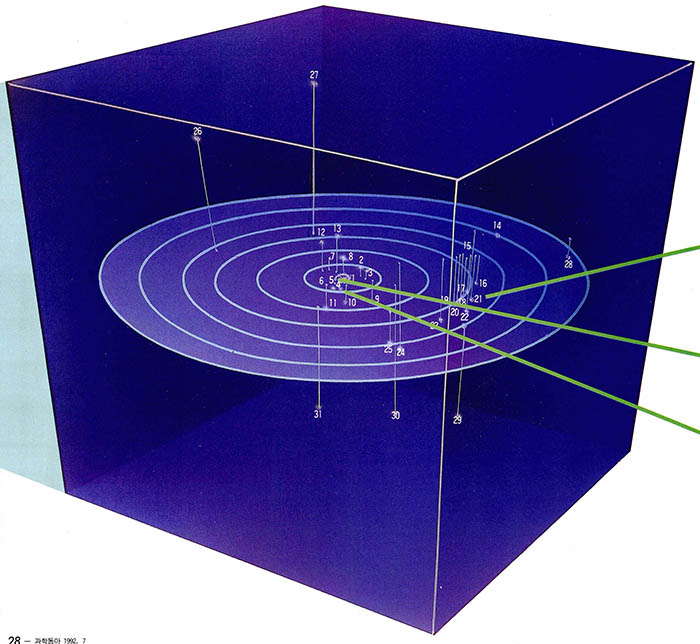
이제까지는 우주의 전체적인 구조(즉 유한과 무한의 문제)나 현재라는 시각에서 볼 수 있는 전 우주의 시공간의 단면(그림1)을 보았다. 이제 시야를 좀 좁혀 우리 지구 근처 수억광년 이내에 은하들의 분포를 알아보자. 어두운 밤하늘에는 대형 망원경으로 관측할 수 있는 외부 은하들이 1천억개 이상 흩어져 있다. 이 은하들은 약 1백50억년간의 긴 시간 동안 서로 중력에 의해 상호작용을 하면서 집단을 형성하고 있다.
이로 인해 천구상에서의 은하들의 분포는 아름다운 형상을 이루고 있는 것이다(그림6). 은하단·초은하단 등의 거대한 은하들의 집단이 여기저기 흩어져 장관을 이루고 있다. 이 각 은하들이 우리에게서 멀어져가는 속도를 측정하면 허블의 법칙에 따라 그들까지의 거리를 알 수 있다. 이 자료로부터 우리는 외부은하들의 3차원적 분포를 볼 수 있는 것이다(그림 1).
여기에서 우리가 알 수 있는 것은 수억광년에 이르는 은하들의 거대구조가 우주에 존재한다는 것이다. 어떻게, 누가 그 큰 구조물을 만들었을까? 이것 또한 현대 천문학자들에겐 커다란 미해결 문제로 남아 있다.