d라이브러리

필요는 발명의 어머니. 양자론의 탄생도 제철업의 요청에서 비롯했다. 그러나 새 이론을 만드는 데는 파격적인 가정과 실험이···

지난번 원자의 구조를 이야기 할때 본 것처럼 19세기는 산업혁명의 여파로 열기관에 관한 연구가 활발했다. 1858년 독일의 '막스 플랑크'역시 뮨헨대학에 진학하면서 열역학에 관심을 갖게 되었다. 당시의 뮨헨대학에는 자유에너지로 잘 알려진 석학 헬름홀쯔 교수가 있었으며 플랑크는 그 밑에서 박사학위를 얻게된다. 뒤에 은사인 헬름홀쯔에게 발탁되어 베를린대학의 교수가 되면서 플랑크는 흑체복사(黑体輻射)의 열역학적 연구에 몰두하게 된다.

플랑크, 흑체복사 연구에 돌입

흑체복사란 무엇인가? 많은 독자들에게는 생소할지 모르지만, 쉽게 말하면 가열된 물질에서 나오는 복사(전자파의 방출)을 말한다. 우리가 주위에서 보는 연탄불에서 나오는 복사, 백열전등에서 나오는 빛 등이 근사적으로는 흑체복사인 것이다. 더 엄밀하게 말하면 모든 빛이 흡수되는, 숯처럼 검은 고체를 가열하였을 때 나오는 복사(빛을 포함한)를 흑체복사라고 한다.

이러한 흑체복사 장치를 만들자면 작은 구멍이 뚫린 공동(空洞 : 속이 비어 있는 상자)을 생각하면 된다. 공동의 작은 구멍을 통해서 들어간 빛(혹은 복사)은 그속에서 반사를 거듭하지 구멍을 통해 다시 나올 가능성은 희박하다. 왜냐하면 공동의 표면적에 비해 구멍의 면적을 지극히 적게 하면 빛이 다시 나올 확률은 아주 작게 되고 이상적인 경우는 확률이 0으로 되기 때문이다. 이 때 빛이 완전히 흡수되었다고 한다. 마치 숯은 검은 색깔이어서 모든 색깔의 빛을 흡수하듯···.

공동과 비슷한 것으로 용광로가 있다.큰 용광로에 비하여 우리가 용광로 속을 들여다 볼 수 있는 구멍은 작으므로 용광로에서 나오는 빛을 흑체 복사라고 보면 크게 틀리지 않는다.

용광로의 온도를 정확히 재려면

기하학(幾何学)의 발달이 고대 이집트 시대의 토지측정에서 시작됐듯이 물리학의 새로운 이론인 양자론의 시초는 공업적인 필요성에서 비롯하였다.

독일은 보불전쟁(1870~71)의 결과 라인강 서안의 석탄 매장량이 풍부한 알사스·로렌 지역을 얻게 되어 이 석탄을 이용하여 제철업이 비약적인 발달을 하고 있었다.그런데 철의 강도와 품질은 용광로의 온도에 매우 민감하였고 따라서 용광로 속의 온도를 정확하게 안다는 것이 품질 개량에 가장 중요한 관건이었다.

지금 같으면 그 흔한 열전대(熱電対 : thermo-couple)로 온도를 측정할 수 있지만 그 당시에는 용광로 속을 들여다 보아 그 빛깔로서 온도를 판단하는 기술자의 예술적인 감각에 의존하고 있었다. 용광로 속이 붉은 색깔이면 약2천도이고 더 흰빛을 내면 몇 도 하는 식이었다. 따라서 이러한 감각에서 탈피하여 과학적인 수단을 발견하기 위하여 흑체복사의 법칙을 연구하게 된 것이다.

물리적인 입장에서는 모든 복사 즉 빛적외선 전파 자외선 X선 및 감마선이 모두가 전자파이고 다만 그 파장이 다를 뿐이다.

예를 들어서 빛(가시광선)의 파장은 0.1㎛(1㎛=1백만분의 1m)정도이고 방송국에서 나오는 FM전파의 파장은 몇십 ㎛이지만 다 같은 전자파이다.

색깔이란 가시광선의 어느 부분의 파장을 보는가에 의하여 결정된다. 만약에 누군가가 흑체복사의 온도와 복사파의 파장 관계를 정확히 계산하여 알 수 있다면 용광로에서 나오는 빛의 파장분포를 밖에서 분광기(分光器)로 측정하여 용광로 속의 온도를 정확히 알 수 있을 것이다. 그 당시에도 프리즘 등 분광(빛을 프리즘을 통하게 하면 무지개처럼 색깔이 분산하는 현상)에 필요한 기구는 있었으므로 흑체복사 스펙트럼을 얻을 수 있었다.

예를 들어 석탄은 평상시에는 검지만 1천℃정도로 가열하면 붉은색(타는 석탄의 색깔, 파장이 약0.7~0.6㎛이 되고 더타서 온도가 올라가면 푸른색으로 변한다.)

실험곡선이 이론에 앞선다
 

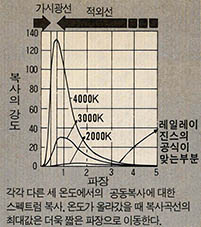
독일의 물리학자 '빈'(Wien)이 이러한 실험을 반복하여 측정한 결과를 그래프로 나타낸 것이 (그림1)이다.

(그림1)에서 보듯이 곡선은 산 모양을 하고 있고 온도가 낮을수록 산의 높이(즉 복사의 강도)가 낮다(이것은 스테판ㅡ볼츠만의 법칙으로 복사의 강도는 온도의 4제곱에 비례한다는 고등학교 교과서에 나와있는 법칙의 결과이다). 이러한 곡선 즉 복사에너지와 온도와의 관계를 처음 이론적으로 계산한 사람은 레일레이(Rayleigh : 1842~1919)와 진스(Jeans : 1877~1946)라는 영국의 두 물리학자였다. ＊『레일레이와 진스는 당시 열역학에서 알려진 법칙을 이용했다. 평형상태에 있는 체계에서는 $\frac{1}{2}$kT(여기서 T는 온도이고 k는 볼츠만 상수)라는 운동 에너지를 독립된 파장의 복사선이 갖는다고 알려져 있었다('독립'이란 2개의 독립된 편광을 말함). 레일레이와 진스는 단위체적당 공동(空洞)의 복사에너지는 진동수에 kT를 곱하여 얻어진다는 것을 알았고(진동수와 파장은 곱이 빛의 속도이며 역수관계에 있다) 다음과 같은 관계식을 제시했다.

E(v)=$\frac{8πν²}{C³}$kT······· (1)

(여기서 ν는 진동수, C는 빛의 속도, E(ν)는 ν라는 진동수에 해당하는 복사 에너지 밀도를 말한다)』

*이 단락은 이해가 되지 않으면 빼고 읽어도 된다.

레일레이와 진스의 공식으로 밝혀진 복사에너지의 법칙은 진동수가 작은 부분의 실험곡선과는 잘 맞았다(그림1 참조). 그러나 이 공식은 ν가 큰 부분에서는 잘 맞지 않고 있었다.

그러나 '빈'교수는 자기의 실험곡선을 두고 여러차례의 실패 끝에 ν가 큰 부분에서는

E(v)=$\frac{8πν²}{C³}$ $\frac{hν}{{e}^{\frac{hν}{kT}}}$········································ (2)

라는 공식이 잘 맞다는 것을 발견했다. 이러한 발전이 독일물리학회에서 발표되는 동안 플랑크교수의 연구실에서 우연한 발견이 이루어졌다.
 

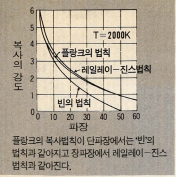
우연한 발견, 에너지는 불연속

플랑크교수의 조수가 우연히도 '빈'의 공식의 분모에서 1을 뺀

E(v)=$\frac{8πν²}{C³}$ $\frac{hν}{e\frac{hν}{kT}-1}$········································ (3)

이라는 공식은 ν와 관계없이 모든 실험값과 맞다는 것을 알았다. 즉 진동수가 크든 작든 혹은 중간이든 간에 플랑크의 공식으로 알려진 위의 식은 실험치와 너무나 잘맞고 있다는 것을 알아낸 것이다.
 

사실상 e$\frac{hν}{kT}$라는 함수는 hν가 kT보다 굉장히 작을 때는 (1+$\frac{hν}{kT}$)으로 되고 따라서 플랑크의 공식은

E(v)=$\frac{8πν²}{C³}$ $\frac{hν}{{e}^{\frac{hν}{kT}}-1}$ ≅ $\frac{8πν²}{C³}$ $\frac{hν}{(1+\frac{hν}{kT})-1}$ = $\frac{8πν²}{C³}$kT가 되어 레일레이ㅡ진스의 공식이 되는것을 알 수 있고 hν가 kT보다 훨씬 큰 진동수가 아주 크게 되면 ${e}^{\frac{hν}{kT}}$는 1보다 훨씬 큰 값이기 때문에 플랑크 공식의 분모에 있는 1은 무시 할 수 있고 따라서 플랑크 공식은 빈의 공식이 된다.

플랑크는 자기의 공식이 낮은 진동수에서는 레일레이ㅡ진스의 공식과 일치하고 높은 진동수에서는 빈의 공식과 일치하는 완전무결한 공식임을 알았다. 그러나 여기서 만족하고 그쳤으면 플랑크 교수는 유명해지지도 않았으려니와 오늘날의 양자론 또한 그 발전이 늦었을 것임에 틀림없다.
 

플랑크 교수는 자기의 공식이 갖는 의미에 대해서 몇년을 두고 곰곰히 생각했다. 파동의 강도는 그 진폭에 비례하고, 진폭은 얼마든지 조절이 가능하므로 파동이 갖는 에너지는 연속적이어야한다. 그런데 플랑크는 만약에, 정말로 만약에 이 에너지가 연속적이 아니고 진동수에 어떤 상수(지금은 플랑크의 상수로 알려져있지만)를 곱한 뛰엄뛰엄한 값만을 가질 수 있다면, 레일레이ㅡ진스처럼 각각의 진동에 해당 에너지를 곱해 모든 진동에 대해 합치는데, 연속적인 경우처럼 적분을 하는 것이 아니라 더해 나갈 때 (수학적인 기호로 ∫대신 ∑를 한다는 뜻) 비로소 플랑크의 공식을 얻을 수 있다는 생각에 도달했다. 다시 말해서 올바른 공식을 위해서는 에너지가 '불연속'이란 가정이 필요불가결하다는 사실을 발견했던 것이다.

이 결과를 독일물리학회에서 발표했을 때 많은 사람들의 반응은 냉담했다. 그러나 이 결과는 곧 아인슈타인, 보아 등 석학에 의하여 확고한 증거가 제시되고 양자론의 시대를 활짝 열게되었다. 그 뒷이야기는 다음호에 계속하겠다.