d라이브러리

맨홀의 비밀은 원의 성질에 숨어 있어요. 원은 오른쪽, 왼쪽, 위, 아래로 돌려도 그 너비(평면인 물체를 가로 지른 거리)가 같은 도형이거든요.

원은 평면 위에 찍은 한 점에서 일정한 거리만큼 떨어진 모든 점의 모임이에요. 원의 가운데에 있는 점O는 ‘원의 중심’이지요. 원의 중심에서부터 원 위에 있는 한 점까지의 거리를 ‘반지름’이라고 해요. 원의 중심을 지나면서 원 위에 있는 두 점을 잇는 선분은 ‘지름’이에요. 지름은 반지름의 두 배이지요. 한 원의 반지름과 지름은 어느 방향에서 재더라도 항상 길이가 같아요. 이러한 성질 때문에 원 모양의 맨홀 뚜껑은 뒤집거나 비스듬히 눕혀도 맨홀 안으로 떨어지지 않지요.

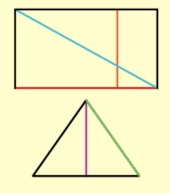
만약 맨홀 뚜껑이 삼각형이나 사각형이라면 어떨까요? 왼쪽 그림처럼 삼각형과 사각형은 어떤 방향으로 선분을 긋느냐에 따라 그 길이가 달라 요. 따라서 비스듬히 눕히거나 세로로 세우면 맨홀 뚜껑의 너비가 맨홀의 너비보다 작아지면서 맨홀 속으로 쑥 빠져버릴 수도 있어요.

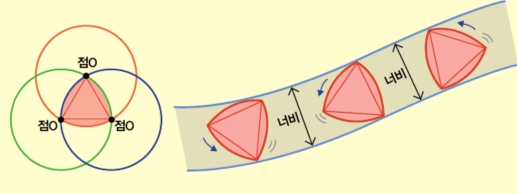
그런데 맨홀 뚜껑으로 사용할 수 있는 삼각형도 있어요. 바로 독일의 공학자 프란츠 뢸로가 발명한 ‘뢸로 삼각형’이에요. 뢸로 삼각형은 반지름이 똑같은 원 세 개가 겹쳐져 만들어지는 도형이에요. 옆으로 빙글빙글 돌려도 그너비가 언제나 일정하지요.

어때요? 무심코 지나치기만 했던 맨홀 뚜껑 속에 숨은 비밀, 자세히 들여 다보고 나니 맨홀이 더 예쁘게 보이지 않나요?