d라이브러리

여기는 <;어린이수학동아>; 탄생 축하 파티가 성대하게 열리고 있는 현장입니다. 아니, 그런데 그 주인공들이 모두 동물이네요. 수학이라면 내로라하는 지구 곳곳의 동물들이 초대를 받고 한자리에 모였다고 합니다. 존재 자체가 수학인 동물부터 수학 능력자 동물까지 모두 모였습니다.

● 비둘기 

비둘기도 사람처럼 숫자를 셀 수 있을까요? 2011년 데미안 스카프 뉴질랜드 오타고대학교 심리학과 박사후연구원은 터치스크린 컴퓨터 화면을 3개 준비했습니다. 그리고 화면마다 다른 모양과 크기, 색깔의 도형을 띄웠습니다. 아래와 같이 첫 번째 화면에는 빨간 타원 1개, 두 번째 화면에는 큰 노란 삼각형 1개와 작은 노란 삼각형 1개, 마지막으로 세 번째 화면에는 길이와 두께가 각기 다른 파란 직사각형 3개를 나타나게 했습니다. 그리고 비둘기들에게 도형의 개수가 가장 적은 화면부터 순서대로 화면을 쪼게 했습니다. 순서를 맞힐 때마다 비둘기들은 먹이를 받았습니다. 

비둘기들이 1부터 3까지 세는 데 익숙해지자 연구진은 화면 속 도형의 개수를 9까지 늘렸습니다. 이런 훈련을 반복한 결과, 비둘기들은 먹이를 주지 않아도 도형의 개수가 적은 순서대로 화면을 쪼기 시작했고, 정답률*은 무려 70%가 넘었어요. 다만, 1과 2처럼 작은 수끼리 비교할 때보다 2와 8처럼 차이가 큰 수끼리 비교할 때 정답률이 더 높았답니다.  

● 황제펭귄

남극의 겨울은 엄청나게 춥습니다. 기온이 영하 35℃ 아래로 떨어지고 바람도 시속 64km 이상으로 불어 가만히 서 있기만 해도 온몸이 얼죠. 황제펭귄은 그런 추위 속에서 알을 낳는 유일한 펭귄입니다. 알을 낳고 지키기 위해서 황제펭귄은 체온을 유지하는 최적의 방법을 선택했습니다. 바로 서로 몸을 맞대고 둥그렇게 모이는 ‘허들링(huddling)’이죠.

2012년 프랑수와 블랑쉐트 미국 캘리포니아대학교 머세드캠퍼스 응용수학과 교수의 연구에 따르면, 황제펭귄은 체온의 손실을 최대한 막기 위해서 육각형의 성질을 이용합니다. 황제펭귄들은 오른쪽 그림처럼 서로의 몸을 밀착합니다. 육각형은 서로 붙여놓았을 때 변과 변이 맞닿아 있어 빈틈이 없죠. 즉, 황제펭귄 한 마리의 몸은 육각형과 같고, 몸과 몸이 촘촘히 닿아있어 차가운 바깥 공기가 덜 스며듭니다. 허들링 구조 안에서 모든 황제펭귄은 최소 2마리에서 최대 6마리의 다른 황제펭귄과 몸을 맞댈 수 있습니다. 

바깥쪽에 서 있는 황제펭귄이 춥지 않겠느냐고요? 맞습니다. 다니엘 지터바트 독일 에어랑엔대학교 연구원이 2011년 발표한 연구에 따르면 황제펭귄들은 30초에서 60초마다 5cm에서 10cm 정도 차례차례 움직입니다. 이 움직임은 아주 미세해 마치 황제펭귄들이 꼼짝하지 않고 그 자리에 서 있는 것처럼 보이죠. 이렇게 바깥쪽에 있던 황제펭귄은 점차 따뜻한 안쪽으로 이동하고, 무리 안에서 체온을 충분히 높인 황제펭귄은 순서에 따라 다시 바깥쪽으로 이동합니다. 

지터바트 연구원이 관찰해보니, 황제펭귄의 허들링은 처음엔 불규칙한 모양에서 시작하지만 움직임을 통해 점차 규칙적인 기하학 무늬를 갖춰간다고 합니다. 황제펭귄의 세계에서 수학이 이렇게 따뜻하고 공평하게 쓰이는군요!   

● 호랑이

호랑이 무늬에는 수학의 규칙이 숨어있어요. 1952년 영국의 수학자 앨런 튜링은 동물마다 털 무늬가 왜 다른지 궁금했어요. 왜 호랑이 털은 줄무늬고 표범은 점무늬인지 알고 싶었던 거죠. 앨런 튜링은 여러 가지 식을 세워 동물 무늬가 어떻게 결정되는지 그 방법을 알아내려고 했어요. 비밀은 배아의 세포 속 피부 색소가 화학 반응할 때 활약하는 확산제와 억제제의 속도 차이에 있다고 보고, 이 과정을 수학 식을 세워 밝혔어요.

 
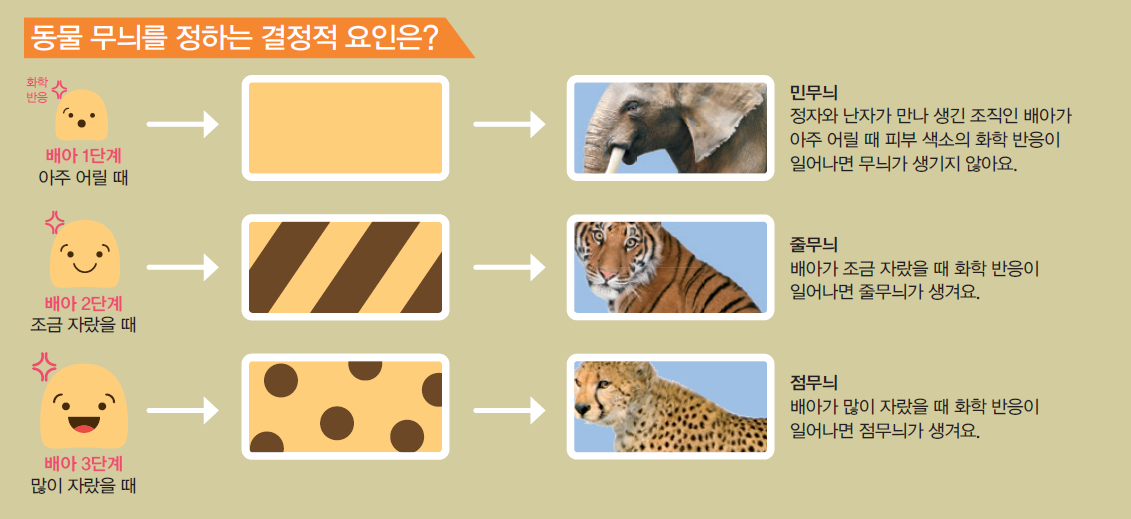
튜링의 이런 아이디어는 1988년 제임스 머레이 영국 옥스퍼드대학교 수리생물학과 교수가 구체화합니다. 우연히 튜링의 아이디어를 본 머레이 교수는 반응-확산 식을 연구해 화학 물질이 반응하는 시기와 배아의 크기에 따라 동물의 무늬가 결정된다는 사실을 알아냈어요. 

●개코원숭이 

개코원숭이는 숫자 1부터 8까지 셀 수 있을 뿐만 아니라 큰 수와 작은 수를 비교할 줄도 알아요. 2013년 5월, 제시카 캔틀런 미국 로체스터대학교 인지과학과 조교수 연구팀은 이 같은 내용을 국제 학술지 ‘심리학 저널’에 발표했어요.  

연구팀은 4~14세 개코원숭이를 대상으로 일종의 게임을 진행했어요. ‘어느 컵에 보상이 가장 많이 들었게!’ 게임이었죠. 연구진은 개코원숭이 앞에 땅콩 수가 다르게 든 컵 2개를 놓았어요. 각 컵에는 땅콩이 1개부터 8개까지 들어있었어요. 개코원숭이는 자신이 고른 컵 속의 땅콩만큼만 먹을 수 있었어요. 연구팀은 이렇게 게임을 총 54회 반복했답니다. 

개코원숭이가 과연 땅콩의 개수 차이를 파악해 더 많은 이득을 얻었을까요? 개코원숭이들은 숫자를 구분할 수 있을 뿐 아니라 큰 수와 작은 수를 비교할 수도 있었답니다. 땅콩 수를 비교해 더 많은 땅콩이 든 컵을 가져갔죠. 그런데 컵 두 개에 든 땅콩 양이 2와 7처럼 눈에 띄는 차이가 날 때는 정답률이 75%에 이른 반면, 6과 7처럼 개수가 비슷할 때는 55%의 확률로 더 큰 수를 골랐어요. 

※ 어수동 탄생 축하 파티를 위해 멀리서 와준 동물 여러분, 정말 감사합니다! 이렇게 많은 동물이 수학적으로 의미가 있는 행동을 한다니, 정말 놀랍습니다. 어수동 친구들도 주변을 찬찬히 둘러보세요. 혹시 우리 집 강아지와 고양이가 수학을 할지도 모르니까요!  

※용어정리

정답률  : 어떤 문제에 대해 정답을 선택한 비율이에요. 10문제 중에 7문제의 정답을 맞혔다면 “이 문제의 정답률은 70%야”라고 
말할 수 있어요.