d라이브러리

새 학년, 새 학기도 수학동아TV와 함께! 안녕하세요, 세 번째 방송으로 찾아온 BJ맹추입니다. 마침내 올 것이 왔군요. 오늘의 수학 개념은 수포자 생성기로 악명 높은 ‘함수’입니다. 함수는 한 달 내내 방송을 해도 모자랄 만큼 할 말이 많은 녀석이지만, 오늘은 ‘함수가 뭘까?’에 초점을 맞춰 진행해 볼 거예요. 자, 그럼 방송 스타~트!

너와 나의 연결고리, 함수

방송이 코앞으로 다가온 어느 날 저녁. 감수성이 폭발하는 새벽 2시. 문득 ‘함수를 한마디로 표현하면 뭘까?’라는 생각이 들어 침대에 누운 채 머리를 굴려봤습니다. 상수, 변수, 함숫값…. 등 복잡한 용어가 잔뜩 떠올랐지만, 제가 내린 결론은 함수는 ‘관계’를 나타내는 수학 개념이라는 겁니다!

삼각관계, 친구 관계처럼 관계는 보통 사람과 사람 사이의 연관성을 나타낼 때 사용하지요. 그런데 꼭 그런 건 아닙니다. 예를 들어 내가 가진 물건은 나와 관계가 있고, 가격이 1000원인 과자는 수많은 수 중 1000과 관계가 있다고 할 수 있으니까요.

이렇게 어떤 대상 사이에 관계가 있고, 이것이 어떤 조건을 만족하면 ‘함수’라고 합니다. 여전히 두루뭉술하다고요? 마침 향긋한 카푸치노가 땡기니, 장소를 카페로 옮겨 이야기를 이어나가도록 하지요!

함수는 1인 1메뉴!

제 친구 다솔, 진호와 함께 카페에서 발견할 수 있는 함수를 찾아보도록 하죠. 이 카페에는 아메리카노, 카페라떼, 카푸치노, 캐러멜 마키아토까지 총 4가지 메뉴가 있습니다. 아직은 저희 세 사람과 메뉴 사이에 아무 관계가 없어요. 이제 저와 다솔, 진호는 취향에 맞게 각각 카푸치노, 캐러멜 마키아토, 아메리카노를 고릅니다.

메뉴를 고른 순간 세 사람과 메뉴 사이에 ‘◯ ◯이(가) 카페에서 고른 메뉴’라는 관계가 생겼습니다. 이 관계를 자세히 나타내면 저와 다솔, 진호라는 손님의 모임이 있고, 다른 한쪽에는 아메리카노, 카페라떼, 카푸치노, 캐러멜 마키아토라는 메뉴의 모임이 있습니다. 이제 저와 카푸치노, 다솔과 캐러멜 마키아토, 진호와 아메리카노를 선으로 이으면 명확해집니다.

이렇게 선택하는 모임과 선택을 받는 모임이 있고, 모임의 구성원 사이에 어떤 관계가 있을 때 이것을 ‘함수’라고 합니다. 명심해야 할 점은 선택하는 모임의 구성원은 반드시 1인 1메뉴를 시킨다는 점이에요. 두 개를 골라도 안 되고, 아무것도 고르지 않아도 안 됩니다. 두 가지 메뉴를 주문하는 것도 하나의 관계지만, 복잡한 관계를 생각하기 전에 먼저 간단한 관계부터 다뤄보자는 거지요!

모든 관계의 대표 f

앞서 예로 든 함수에서 저와 다솔, 진호의 모임과 메뉴의 모임은 ‘카페에서 선택한 메뉴’라는 관계로 이어져 있습니다. 만약 누가 ‘다솔이가 고른 메뉴가 뭐야?’라고 물으면 다솔이와 이어진 메뉴를 확인한 뒤, ‘캐러멜 마키아토’라고 대답하면 될 거예요.

매번 선으로 잇는 게 귀찮았는지, 1734년 수학자 레온하르트 오일러는 함수를 뜻하는 영어 단어 function의 첫 글자인 f 와 괄호 (, )를 이용해 함수를 더 효율적으로 나타냈어요. 자판기에서 버튼을 누르면 버튼에 적힌 이름과 관계 있는 음료수가 나오는 것처럼, f ( )라는 자판기의 괄호 안에 이름을 넣으면 관계 있는 메뉴가 ‘뿅’하고 나오는 겁니다.

오일러는 누가 어떤 메뉴와 이어졌는지 구구절절 설명하지 않고 f 라고만 표시했어요. 만약 ‘진호’를 넣으면 메뉴 중에 진호와 ‘카페에서 고른 메뉴’라는 관계로 맺어진 아메리카노가 나오는 거예요. 이것을 오일러가 고안한 기호로 표시하면 ‘f (진호)=아메리카노’가 되는 거지요!

수와 수의 관계는 특별하다

학교에서 배우는 함수도 카페에서 메뉴를 고르는 함수와 다를 바 없습니다. 차이가 있다면 두 모임이 모두 수로 이뤄져 있고, f 가 이 수들의 관계를 나타낸다는 거지요. 갑자기 수가 나오니 복잡해 보이나요? 정반대입니다! 모임의 구성원이 수면 함수를 간단하게 표현할 수 있거든요.

오른쪽 위에 있는 그림처럼 저와 다솔, 진호에게 번호를 매겨 각각 1, 2, 3으로 표시하고, 메뉴는 카페모카, 카푸치노, 캐러멜 마키아토, 아메리카노 순으로 1, 2, 3, 4로 표시했다고 해보죠. 이제 이름과 메뉴명 대신 번호를 이용하면 이 함수는 f (1)=2, f (2)=3, f (3)=4라고 표시할 수 있어요.

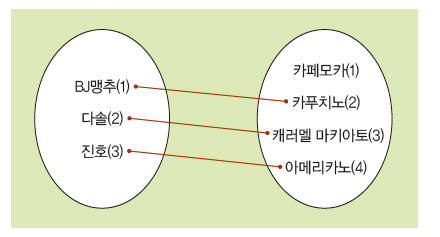
어떤가요? 길이가 짧아졌다는 게 가장 눈에 띄지만, 더 좋은 점은 저, 다솔, 진호의 번호와 관계있는 메뉴의 번호가 항상 1만큼 크다는 사실을 이용해 이 함수를 f (x)=x+1로 적을 수 있다는 겁니다.

x대신 1, 2, 3 중 하나를 대입해 계산해 보세요. f (3)=3+1=4니까 진호(3)는 4에 해당하는 아메리카노를 골랐다는 걸 곧장 알 수 있잖아요! 이때 x는 번호 1, 2, 3 중 어떤 수로든 변할 수 있으니까 특별히 ‘변수’라고 부르고, x와 ‘관계’있는 수 f (x)를 함숫값이라고 불러요.