d라이브러리

지도에 적군의 진지를 표시하고, 어떻게 적군을 공격할지 의논하려면 정확한 지도가 필요해. 우리가 살고 있는 지구는 구 모양이기 때문에 정확히 말하면 평면이 아닌 곡면이야. 지도를 만들려면 곡면인 지구를 평면으로 표현해야 한다는 얘기지. 그렇지만 모양, 거리, 넓이, 각도 등을 모두 왜곡 없이 평면에 나타내는 것은 불가능한 일이야. 그래서 사람들은 필요한 목적에 따라 최대한 지도를 정확하게 만들려고 노력했어. 그러다 보니 자연스럽게 기하학이 발전하고 새로운 기하학도 탄생했지.

구 모양 지구를 평면에 나타내기 위해 구를 원통에 넣은 뒤 빛이 원통에 비춰서 생긴 그림자로 지도를 그렸어. 원통투영법이라고 해. 원통투영법에는 크게 두 가지가 있는데, 메르카토르투영법과 횡축 메르카토르투영법이야.

횡축 메르카토르투영법은 같은 원통투영법이지만 메르카토르투영법과 조금 달라. 우선 원통을 90° 회전한 상태에서 지구의 한 경선(세로선)과 원통의 단면인 원이 일치하도록 맞춘 뒤 투영한 방법이지. 이렇게 하면 그 경선 근처에서는 지형의 오차가 작다는 장점이 있어서 특정 지역의 지형도를 만들 때 주로 횡축 메르카토르투영법을 이용해.

이처럼 지도를 만들 때 투영법은 중요하고 또 기본이 되는 원리야. 이런 투영법이 발달하면서 사영기하학이라는 새로운 기하학이 탄생했어. 사영기하학의 선구자인 프랑스의 퐁슬레는 나폴레옹 전쟁에 참전했다가 포로가 됐어. 수용소에 있을 때 벽을 공책으로 삼고 난방을 위해 지급된 숯을 이용해서 사영기하학 연구했다고 해. ‘사영’이란 한자로 쏠 ‘사’, 그림자 ‘영’을 써. 빛을 쏘아 만든 그림자란 뜻으로 투영과 사영은 비슷한 말이야.

혹시 교실에 있는 프로젝터 기계를 아니? 영상을 큰 화면에 투영해 여러 사람이 볼 수 있게 만든 이 기계는 사영기하학의 원리를 나타낸 것이라고 볼 수 있어. 사영기하학은 입체 영상이나 사진, 그림 등에서 많이 쓰는데, 그 창시자가 전쟁 가운데 포로로 있을 때 연구한 것이라니 수학은 시기와 장소를 가리지 않고 발전하는 학문 같아.

몰바이데도법
 

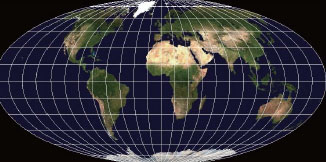
1805년 독일의 천문학자 몰바이데가 만든 지도법이야. 몰바이데도법으로 만든 지도는 면적의 비율이 실제와 같다는 장점이 있지. 그리는 방법은 적도에 해당하는 긴 지름과 극과 극을 연결하는 중앙경선의 비를 2:1로 한 타원으로 지구 윤곽을 그린 뒤 일정한 간격으로 경선을 타원형 곡선으로 그려. 중앙에서 멀어질수록 곡선의 휜 정도가 커지겠지. 이렇게 해서 지도를 그리면 면적의 비율이 비교적 정확한 지도를 만들 수 있어.



▼관련기사를 계속 보시려면?

수학을 알면 축구가 보인다
PARTⅠ 수학을 알아야 축구를 잘 한다 : 축구는 수학이다
PART Ⅱ 수학으로 월드컵을 예측한다 : 누가누가 이길까?
전쟁에서 꽃 피운 수학
작전명령 ① 대포를 정확하게 쏴라!
작전명령 ② 정확한 지도를 만들어라!
작전명령 ③ 최선의 방법을 찾아라!
작전명령 ④ 더 빠르고, 더 정확하게!