d라이브러리

평화로운 어린이수학동아 편집부에 논쟁이 벌어졌어요. 
이게 다 김연진 기자가 편집부에 던진 ‘각뿔의 꼭짓점’ 문제…, 아니, M몬스터 숲에 사는 꼭짓점 몬스터 때문이에요. 
무슨 일인지 알아보러 가볼까요?

김기자의 사건일지 ① 원뿔의 꼭짓점의 정의는? 

김 기자는 5월 15일자 놀이북 ‘M몬스터를 잡아라! : 변신의 귀재, 꼭짓점 몬스터’ 원고를 쓰고 있었어요. 꼭짓점 몬스터 수학 카드 뒷면에 쓸 꼭짓점의 정의를 정리하는 중이었답니다. 평면도형에서 꼭짓점은 ‘각을 이루고 있는 두 변이 만나는 점’이고, 입체도형에서 꼭짓점은 ‘모서리와 모서리가 만나는 점’이라고 원고를 작성했어요. 그리고 다양한 도형을 꼭짓점의 정의와 함께 소개했답니다.
그런데 원뿔을 자세히 보니 입체도형의 꼭짓점에 대한 정의가 이상하게 느껴졌어요. 원뿔은 입체도형인데, 원뿔의 꼭짓점은 모서리와 모서리가 만나는 점이 아니니까요.

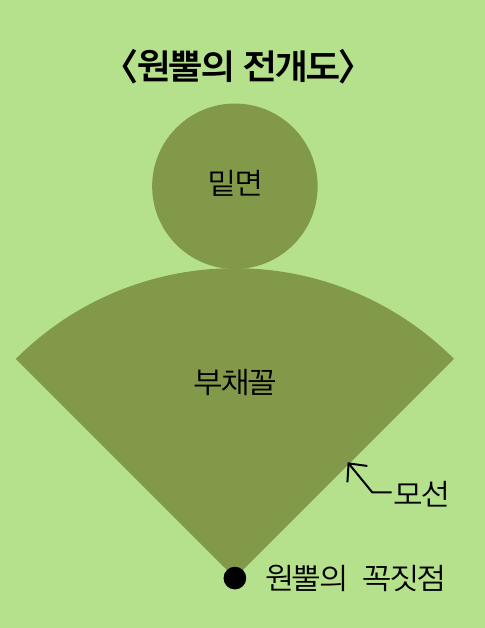
‘원뿔의 꼭짓점’은 원뿔에서 뾰족한 점으로 1개예요. 더 정확하게 말하면 원뿔의 전개도에서 부채꼴의 중심이에요. 그래서 꼭짓점의 정의에 대해 다시 알아보게 됐고, ‘각뿔의 꼭짓점’은 삼각뿔을 제외하고는 언제나 한 개라는 글을 보게 됐어요.

혼란의 시작은 원뿔이었지만, 고민은 각뿔로 이어졌어요. 모서리와 모서리가 만나는 점이 꼭짓점이라면 사각뿔의 꼭짓점은 5개여야 하잖아요. 혼란에 빠진 기자는 사각뿔 사진을 들고 편집부를 돌아다니기 시작했어요. “각뿔의 꼭짓점은 몇 개일까요?” 기자들의 답변은 5개와 1개로 갈렸어요. “하나, 둘, 셋, 넷, 다섯! 꼭짓점은 총 5개예요.” 다른 기자는 위로 뾰족하게 솟은 점을 가리키며 말했어요. “‘각뿔의 꼭짓점’은 모든 옆면이 공통으로 만나는 점이니 1개예요.” 

불붙은 ‘각뿔의 꼭짓점’ 논란! 과연 누구의 말이 맞는 걸까요?

김기자의 사건일지 ② 헷갈리는 게 당연해! ‘각뿔의 꼭짓점’ 

 앞서 낸 문제에 다른 대답을 한 두 기자는 문제를 다르게 이해했어요. 최은혜 기자는 사각뿔에서 ‘꼭짓점’의 개수를 찾는 문제라고 생각했어요. 각뿔에서 꼭짓점의 개수는 밑면의 변의 수에 1을 더해 구할 수 있어요. 박건희 기자는 ‘각뿔의 꼭짓점’을 찾는 문제로 파악했기 때문에 1개라고 답했어요. 

초등수학 교육 전문가에게 취재해 보니 ‘각뿔의 꼭짓점’과 ‘꼭짓점’은 정의가 다른데 용어가 비슷해 최은혜 기자가 문제를 잘못 이해한 걸로 밝혀졌어요.

각뿔에서 모서리와 모서리가 만나는 점을 ‘꼭짓점’이라고 해요. 꼭짓점 중에서도 옆면이 모두 만나는 점이 ‘각뿔의 꼭짓점’이에요. 각뿔에서 밑면에 있지 않은 꼭짓점이라고도 볼 수 있지요. ‘각뿔의 꼭짓점’은 각뿔의 높이를 재는 데 사용해요. ‘각뿔의 꼭짓점’에서 밑면에 수직인 선분의 길이가 높이거든요. ‘각뿔의 꼭짓점’도 꼭짓점의 하나예요. 

삼각뿔을 제외하고는 ‘각뿔의 꼭짓점’ 개수는 모두 1개예요. 삼각뿔은 모든 면이 삼각형이기 때문에 어떤 면을 밑면으로 두는가에 따라 ‘각뿔의 꼭짓점’이 달라져요. 입체도형에서 밑면은 높이를 재는 방향과 수직인 면을 말해요. 삼각뿔은 어떻게 놓느냐에 따라 네 면 모두 밑면이 될 수 있어요. 따라서 삼각뿔의 네 꼭짓점 모두가 ‘각뿔의 꼭짓점’이 될 수 있어요. 

하지만 사각뿔, 오각뿔, 육각뿔 등 다른 각뿔은 옆면과 밑면의 모양이 달라서 밑면이 하나예요. 밑면의 모양에 따라 사각뿔, 오각뿔 등으로 불리고, 각뿔의  밑면은 각뿔의 꼭짓점과 닿지 않는 면이에요. 따라서 ‘각뿔의 꼭짓점’도 바뀌지 않아요.

서울증산초등학교 강경은 교사는 ‘각뿔의 꼭짓점’을 ‘밑면과 가장 먼 꼭짓점’으로 볼 수 있다고 설명했어요. 또한 ‘각뿔의 꼭짓점’에 관한 문제는 개수를 묻기보단 그림에서 ‘각뿔의 꼭짓점’을 찾아 표시하는 문제로 종종 나온다고 말했어요.

우리나라도 영어권 국가처럼 ‘꼭짓점’과 ‘각뿔의 꼭짓점’을 완전히 다른 단어로 구분하면 좋았을 것 같아요. 교과서 만드는 분들, 어수동 참고해서 ‘각뿔의 꼭짓점’과 ‘꼭짓점’의 구분을 좀 더 명확히 해주세요!