
EFFECT
특이한 효과
1887년 독일의 물리학자 하인리히 헤르츠는 금속판에 빛을 쬐면 전자가 튀어나오는 현상을 발견했다. 바로 광전효과다. 금속판의 전자는 금속 원자와의 상호작용으로 묶여있기 때문에 저절로 금속판을 벗어날 수 없다. 충분한 에너지를 가진 빛을 밖에서 쪼여줘야만 전자가 금속판을 박차고 튀어나올 수 있다. 여기까진 별로 신기할 것이 없다. 당시 물리학자들도 마찬가지였다.
그런데 금속판을 튀어 나온 전자의 운동에너지가 빛의 세기(빛을 이루는 전기장 혹은 자기장의 강도)에는 전혀 상관없이 오직 빛의 진동수에만 비례한다는 실험결과가 나왔다. 물리학계는 당혹감에 휩싸였다. 진동수가 특정한 기준 이하로 작은(파장이 긴) 빛은 아무리 강한 세기로 비춰도 전자가 튀어나오지 않았다. 반면 진동수가 기준 이상으로 큰(파장이 짧은) 빛은 아주 약하게만 쪼여도 전자가 바로 튀어나왔다. 빛을 파동으로 해석하는 고전전자기학으로는 설명할 수 없는 현상이었다. 예컨대 아무리 붉은 빛을 강하게 쪼여도 흐르지 않던 전류가, 아주 약한 푸른 빛을 쏴 주자마자 흐르기 시작하는 현상은, 정말 신기했지만 누구도 설명하지 못했다.
1905년 아인슈타인은 플랑크가 크게 주목하지 않았던 에너지 양자 개념을 이용해 광전효과를 성공적으로 설명해냈다. 플랑크상수(h)와 빛의 진동수( f)의 곱(hf)을 빛의 에너지 단위로 쓰자는 제안이었다. 이방법에 따르면 빛의 에너지는 hf, 2hf, 3hf, … 처럼 띄엄띄엄 떨어져 있는, 혹은 하나씩 더할 수 있는 값처럼 보인다. 물리학에선 이 ‘무언가’를 빛알(광자)이라고 부른다. 전통적인 파동설에서 벗어나, 빛의 본질을하나씩 셀 수 있는 알갱이로 보는 관점이다.
아인슈타인은 빛알 개념을 통해 광전효과를 완벽히 해석했다. 그의 설명은 다음과 같다. 전자가 금속판에서 튀어나오려면 일함수 W보다 큰 에너지가 필요하다. 그런데 진동수가 f인 빛알 한 개의 에너지(hf)가 W보다 작으면, 빛의 세기가 아무리 커도 전자는 튀어나오지 않는다. 빛의 에너지는 빛의 세기와 관련이없고, 오직 진동수( f)에만 비례하기 때문이다. 만약 빛의 에너지가 W보다 크면 전자는 hf - W만큼의 운동에너지를 갖고 금속판을 벗어나게 된다. 이땐 빛의 세기가 아무리 약해도 전자를 탈출시킬 수 있다.


백열전구에서 나오는 빛의 에너지를 2W, 파장을 500nm정도로 어림해서 계산하면, 1초마다 나오는 빛알의 수는 무려 1032개가 넘는다. 빛을 띄엄띄엄한 입자모임으로 파악하기가 어려운 이유다.
CRACKS
띄엄띄엄 드러난 균열
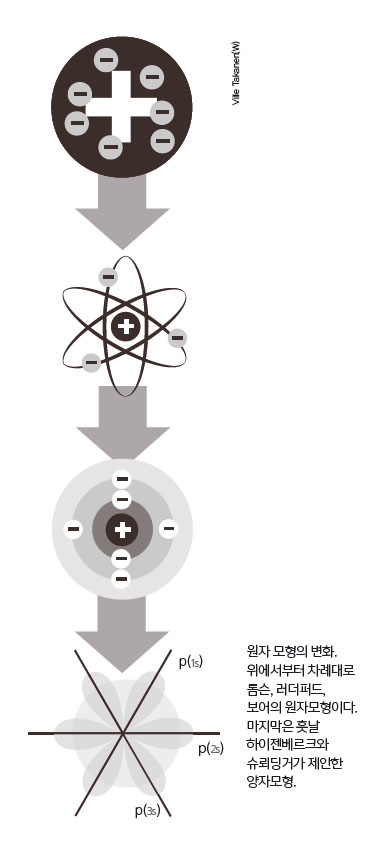
당시는 광전효과뿐만 아니라 고전물리학의 균열도 띄엄띄엄 드러나던 시대였다. 예를 들어보자. 고루 퍼져 있는 양전하에 군데군데 전자가 박혀 있다고 본 톰슨의 원자 모형은, 원자핵을 발견한 러더퍼드의 산란실험으로 무너졌다(9월호 상수의 탄생 참고). 마침내 물질의 구조를 완전히 이해했다는 기쁨도 잠시, 러더퍼드의 발견은 그때까지 견고하다고 믿었던 고전물리학에 치명상을 입히게 된다.
양전하를 띤 원자핵과 음전하를 띤 전자 사이에는, 쿨롱의 전기력이 서로를 잡아당기는 방향으로 작용한다. 보편중력의 영향으로 지구가 태양 주위를 공전하는 것처럼, 전자가 원자핵 주위를 빙글빙글 돌고 있다. 그런데 지구와 달리 전자는 전하량을 가지고 있다. 맥스웰이 완성한 고전전자기학(8월호 상수의 탄생 참고)에 따르면, 가속운동하는 전하는 전자기파를 계속 발생시킨다(움직이는 방향이 계속 달라지는 원운동도 가속운동이다). 따라서 원자핵 주위를 도는 전자는 전자기파를 계속 발생시키고, 전자의 운동에너지는 점점 줄어든다. 고전물리학은 이처럼 전자기파로 빼앗긴 에너지로 인해 원운동 궤도가 점점 작아지면서, 결국 전자가 원자핵에 충돌해 하나가 될 거라고예측했다. 하지만 우리의 몸이 늘 멀쩡한 데에서 알수 있듯, 그런 일은 벌어지지 않는다.

MODEL

세상의 구조
이제 오늘의 주인공, 덴마크의 물리학자 닐스 보어가 등장할 차례다. 1913년 보어는 당시 물리학이 풀지 못하고 있던 문제들을 한방에 해결할, 새로운 원자모형을 제시했다. 보어의 원자모형은 다음과 같은 가정 위에 세워졌다.

보어는 쿨롱의 전기퍼텐셜 에너지를 고려한 고전적인 수식에 이 가정들을 적용해, 수소원자에 묶여 있는 전자가 띄엄띄엄한 에너지 값만을 가질 수 있음을 증명했다. 보어의 모형은 뤼드베리가 발표한 불연속적인 수소 스펙트럼도 정확히 설명했다. 또한 수소원자의 전자가 가질 수 있는 최소한의 궤도 반지름이 있고, 이보다 작은 반지름을 가질 수 없다는 사실도 밝혀냈다. 이 반지름을 보어 반지름이라 부른다. 즉 보어 반지름을 따라 원자핵을 도는 전자는 가장 낮은 에너지 상태에 있는 것이다. 이때의 각운동량(L1= ħ)으로부터 전자의 자기 모멘트를 구할 수 있다. 이를 보어 마그네톤이라고 한다(INSIDE 참조). 궤도운동을 하는 전자가 가질 수 있는 가장 작은 자기 모멘트 값이다.
보어의 원자모형은 이처럼 많은 난제를 해결했지만, 여전히 이론적으로는 논란이 있었다. 슈뢰딩거와 하이젠베르크가 양자역학을 완성한 뒤에야 보어의 원자모형도 체계적인 이론이 됐다. 아직 우리에겐 더 많은 이야기가 남아 있다.











