d라이브러리

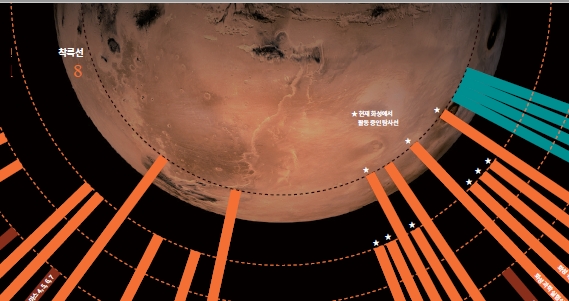
2014년 8월 서울에서 개최될 세계수학자대회의 하이라이트는 수학계의 노벨상이라 불리는 필즈상 수상식이다. 필즈상은 40세 이하의 수학자에게 주는 상인데, 4년에 한번 시상하므로 매년 수상자를 내는 노벨상보다 희소성이 높다.


이토록 귀한 필즈상 메달에는 아르키메데스(BC. 287~212년)의 얼굴이 새겨져 있다. 수학사를 통틀어 최고의 수학자 3인방은 아르키메데스, 뉴턴, 가우스라는데, 왜 하필 필즈상은 아르키메데스를 선택했을까? 뉴턴과 가우스는 각각 17세기와 19세기에 활동했고 누가 뭐래도 르네상스 시대까지는 아르키메데스가 최고의 수학자였기 때문이다. 게다가 아르키메데스는 이론뿐 아니라 응용까지 아우른 수학의 대가였다.


 

[아르키메데스가 새겨져 있는 필즈상 메달.]

중세 기도문에 가려진 아르키메데스의 ‘방법’


아르키메데스는 고대 그리스의 도시 국가 ‘시라쿠사’에서 천문학자의 아들로 태어났다. 그는 젊은 시절 알렉산드리아에서 공부했고 시라쿠사로 돌아와 다양한 분야의 연구와 발명을 하다가 생을 마쳤다. 아르키메데스가 남긴 연구물 중 특히 중요한 논문은 ‘방법(The Method of Mechanical Theorems)’이다. 아르키메데스가 쓴 편지 형식인데, 이 논문을 되찾아 내용을 밝힌 과정은 마치 한 편의 영화와 같다.


종이가 발명되기 전, 중세 유럽과 아라비아에서는 양피지에 글을 적었다. 그런데 양피지는 무척 귀해서 불필요하다고 판단되는 내용은 폐기하고 그 위에 덧쓰는 경우가 많았다. 이를 ‘팰림프세스트’라고 한다. ‘방법’ 역시 팰림프세스트의 운명을 겪게 됐다. 10세기 경 양피지에 쓰인 이 논문은 13세기에는 가치가 없다고 여겨져 중세 기도서로 변신됐다. 그토록 중요한 논문이 폐기된 것은 큰 불행이었지만, 기도서로 바뀐 덕분에 온전히 보존될 수 있었다는 점은 한편 다행이었다.


 

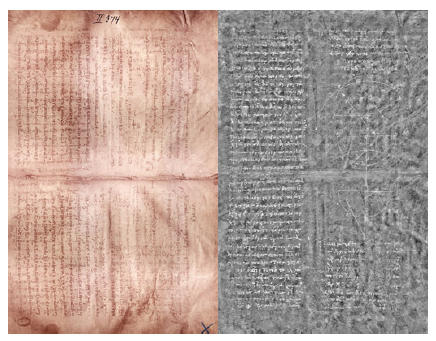
[중세 기도문(왼쪽)과 그 안에 숨겨져 있던 아르키메데스의 ‘방법’.]

덴마크의 문헌학자 하이베르그(1854~1928년)는 터키 이스탄불에서 이 논문을 발견했다. 그는 중세 기도서가 새겨진 양피지에 미세한 흔적으로 남아 있는 글을 해독해 원래 아르키메데스의 논문이었음을 알아냈으며, 돋보기로 일일이 작업해 논문 내용의 80%를 해독하고 1910년 번역본을 출간했다. 그런데 ‘방법’의 기구한 운명은 여기서 그치지 않았다. 이 양피지는 세계대전이 일어났을 때 다시 사라졌고 1998년이 돼서야 뉴욕 크리스티 경매에 등장했다. 익명의 수집가가 200만 달러에 구입했고, 그는 첨단기법을 이용해 논문의 내용 거의 전부를 복원해 냈다.


이 논문에서 오늘날 가장 주목받는 것은 ‘평형법’을 이용해 구의 부피를 구하는 내용이다. 한 쪽에 원기둥, 다른 한 쪽에 구와 원뿔이 평형을 이루고 있다고 놓고, 적분 아이디어를 무척 기발하게 적용했다. ‘소화불량을 일으킬 정도의 난제’라는 뜻의 ‘스토마키온’도 포함돼 있는데, 이는 정사각형을 14조각으로 나눈 퍼즐로, 이 조각들을 배열해 다양한 사물, 동물, 식물의 모양을 만들어낼 수 있다. 이 퍼즐로 정사각형을 만드는 경우는 한 가지가 아니다. 아르키메데스는 정사각형을 만드는 방법의 수를 계산했는데, 이는 경우를 체계적으로 따지는 조합론 연구와 맞닿아 있다.

 

[14개의 조각으로 다양한 모양을 만드는 ‘스토마키온’. 아르키메데스가 계산한 정사각형 만드는 방법의 수는 조합론 연구와 맞닿아 있다.]






2003년 퍼즐 연구자인 빌 커틀러는 컴퓨터를 돌려서 14조각으로 정사각형을 만드는 방법은 1만7152가지고, 회전과 대칭이동을 시켰을 때 같아지는 것들을 제외하면 총 536가지의 다른 배열이 가능하다는 것을 밝혀냈다. 배열의 개수인 536으로부터 5월 36일을 연상한 수학자들은 36일이 5월 31일 이후 다섯 번째 날이므로 6월 5일을 아르키메데스의 날이라고 부르자는 제안을 내기도 했다.


 

[이탈리아의 줄리오 파리지가 1599~1600년 사이에 그린 벽화. 아르키메데스가 포물면 거울로 햇빛을 모아 로마의 목조 전함을 태웠다는 내용을 담고 있다. 그러나 햇빛을 반사시켜 로마군의 시야를 방해했다는 게 더 설득력 있다.]



역사상 가장 위대한 수학자의 최후


아르키메데스의 고향인 시라쿠사는 당시 로마와 전쟁을 했다. 그런 현실 때문에 아르키메데스는 독창적인 무기도 다수 발명했다. 적의 배가 성벽 가까이 접근했을 때 무거운 돌을 떨어뜨리는 투석기, 배를 바다에서 끌어올리는 기중기 등이 있다. 포물면 거울을 이용해 햇빛을 모아 로마의 목조 전함을 태웠다는 설도 있는데, 그보다는 포물면 거울로 햇빛을 모아 반사시켜서 로마군들의 눈을 일시적인 실명 상태로 만들었을 것이라는 설명이 더 설득력 있어 보인다.


이런 아르키메데스의 신형 무기에 힘입어 시라쿠사는 2년 가까이 로마에 맞서 버텼다. 그러나 어느새 자만심을 갖게 되어 아르테미스 여신을 기리는 축제를 성대하게 벌였고 이를 틈타 로마군은 시라쿠사를 공격했다. 술에 취해 자고 있던 시라쿠사의 군사들은 제대로 저항도 하지 못하고 패배했다.


당시 로마의 장군 마르켈루스는 아르키메데스의 명성을 익히 들었기에 그를 죽이지 말라고 신신당부했다. 그러나 결국 아르키메데스는 로마 군사에게 살해당한다. 이에 대해서는 여러 설이 있다. 유력한 설에 따르면, 로마군이 시라쿠사를 점령했을 때 아르키메데스는 그 사실을 모른 채 모래 위에 도형을 그리며 연구에 몰두하고 있었는데 로마 병사가 다가오자 “내 원을 건드리지 말라”고 소리쳤고 이에 격분한 로마 병사가 그를 찔러 죽였다. 또 다른 설에 따르면, 로마 병사가 아르키메데스를 발견하고는 마르켈루스에게 가자고 요청했는데, 아르키메데스는 당시 숙고하고 있던 문제를 끝마치기 전에는 갈 수 없다고 반항했고 이에 분개한 병사가 그의 목을 베었다. 프랑크푸르트 시립 미술관에 가면 아르키메데스의 최후를 묘사한 모자이크 작품을 볼 수 있다. 로마 병사가 칼을 뽑아들고 아르키메데스를 위협하고 있는 이 작품은, 고대에 제작된 것을 18세기에 재연한 것이다.


설은 여럿이지만, 공통적으로 마르켈루스가 아르키메데스의 죽음을 애통해 했다고 전하고 있다. 마르켈루스 장군은 그의 묘비에 구와 외접하는 원기둥 그림을 새겨 넣었는데, 아르키메데스의 유지를 받든 행동이었다. 아르키메데스의 또 다른 논문 ‘구와 원기둥에 대하여’에 실린 53개의 명제 중 ‘구의 부피는 외접하는 원기둥의 부피의 3분의 2이고, 구의 겉넓이 역시 외접하는 원기둥의 겉넓이의 3분의 2’라는 내용이 있는데, 아르키메데스는 이 발견을 대단히 자랑스럽게 생각해 구와 외접하는 원기둥 그림을 자신의 무덤에 새겨달라고 생전에 요청했던 것이다.


그 후 그의 무덤은 논문처럼 기구한 운명을 겪었다. 오랜 세월이 흐른 기원전 75년, 로마의 정치가 마르쿠스 키케로는 아르키메데스의 무덤을 찾으려고 했다. 수많은 무덤을 모두 조사한 끝에 무성하게 자란 관목 위로 솟아 나온 아르키메데스의 묘비석을 찾았고 무덤 주위를 복원했다. 이런 관심은 얼마 동안은 계속됐지만, 이 무덤은 또 다시 잊혀졌다. 2000년이 흐른 1965년, 그의 무덤은 시칠리아 시라쿠사에서 호텔 기초 공사를 하던 중 또 다시 극적으로 발견됐다.


 

“누가 아르키메데스의 명성을 택하지 않겠는가?”


아르키메데스를 기리는 다양한 명언이 있다. 아일랜드의 수학자 해밀턴은 “누가 정복자 마르켈루스의 명성보다 아르키메데스의 명성을 택하려 하지 않겠는가?”라고 말했다. 수리철학자 화이트헤드는 그리스와 로마를 비교하면서 “어떠한 로마인도 기하학의 도형을 고찰하다가 죽은 이는 없다”고 감탄의 말을 남겼다. 로마는 그리스와 같이 학문적 발전을 이루기보다는 그리스가 남겨준 여러 수학과 과학 이론을 실용화하는 수준에 그쳤다는 점을 잘 드러낸 말이다. 영국의 수학자 하디는 “그리스의 비극 시인 아이스킬로스는 잊혀져도 아르키메데스는 기억될 것이다. 왜냐하면 언어는 사라져도 수학적 아이디어는 영원하니까!”라고 말했다. 볼테르는 “호머보다도 아르키메데스의 머릿속에 더 풍부한 상상력이 있다”고 극찬했다. 이런 표현은 수학사에서 아르키메데스가 차지하는 명성을 잘 보여준다.