d라이브러리

무엇인가 정보를 찾아보기 위해서 각종 포털을 검색해본 사람은 구글(Google)이 다른 포털과는 다르다는 점을 느꼈을 것이다. 대부분의 포털은 화면에 특정 검색어를 집어넣었을 때 보여주는 순서가 사람들이 기대하는 순서와 다르다. 광고비를 내는 회사가 검색결과 앞부분에 뜨도록 해주는 경우가 있기 때문이다. 포털에 돈을 지불하는 그런 회사들은 ‘스폰서’라는 이름으로 따로 보여주는 것이 옳은데 스폰서라는 것을 감추고 검색등수를 조작하기도 한다.

중소기업은 구글 검색등수에서 밀려나면 회사가 흔들릴 만큼 매출액이 감소할 수 있기 때문에 구글을 상대로 소송을 걸기도 하고 고객 사이트의 검색등수를 올려주는 자문회사까지 있다. 어떤 사람은 높은 등수를 만들어낸 뒤에 그 사이트를 팔아넘기기도 한다. 구글이 이렇게 권위를 갖게 된 배경에는 다른 영향에 휘둘리지 않고 수학 원리에 기반해 자체 개발한 알고리듬을 충실하게 따랐기 때문이다.

중요한 사이트 찾는 알고리듬
구글에서 보여주는 검색등수는 ‘페이지랭크’(PageRank)라는 이름의 알고리듬 계산 결과인데, 대략 이런 식으로 작동한다. 어느 사이트가 다음 두 가지 중에서 하나를 가지고 있으면 다른 사이트보다 중요하다고 할 수 있다.

(1) 권위가 있다. 예를 들어 대학이나 정부기관 또는 방송국 홈페이지에 나오는 정보는 다들 믿어준다. 사람들이 그 사이트에서 자기 쪽으로 링크되길 원한다는 의미다.

(2) 소위 ‘마당발’ 사이트다. 포털을 예로 들면 사람들은 무엇이든 우선 포털에서 찾기 시작한다. 많은 사이트로 나가는 링크를 갖고 있기 때문이다.

뒤집어 생각하면 권위 있는 사이트에서 내 홈페이지로 연결되는 링크가 있고, 포털 등 마당발 사이트에도 내 홈페이지로 연결되는 링크가 있다면 나의 등수는 대단히 높을 것이다. 어느 모임에서건 회장과 총무를 개인적으로 알고 있으면 ‘왕따’가 되지 않는 것과 같다.

그런데 검색결과를 일렬로 보여줘야 하기 때문에 (1)번 성질을 가지는 곳과 (2)번 성질을 가지는 곳을 어떤 순서로 보여줘야 하는지 생각해봐야 한다.

예를 들어 100명의 사람들이 1만 원씩 갖고 있다가 자기가 원하는 사람들에게 n분의 1씩 똑같이 나눠주는 상황을 설정해보자. 돈 대신에 자신의 영향력을 나눠준다고 생각하거나 일종의 인기투표를 한다고 생각해도 된다. 만일 은숙이가 네 명의 친구들에게 나눠준다면 1/4인 2500원씩 줄 것이고, 경수가 한 명에게만 준다면 1만 원을 다 줄 것이다. 모두들 자기가 가진 돈 1만 원을 나눠주면 돈이 몰리는 사람들이 있게 마련이고 인기도(또는 중요도)를 알 수 있다.

분배 비율에서 중요도 계산할 수 있어

100명의 중요도를 계산하는 과정은 지면에 나타내기에 번거롭기 때문에 네 사람이 있는 경우를 생각해보자. 4명 가운데 톰은 메리, 찰스, 수잔을 다 좋아하고 메리는 찰스만 좋아한다. 한편 찰스는 수잔만 좋아하고 수잔은 톰과 찰스를 좋아한다. 이들의 선호도를 화살표로 나타내면 톰, 메리, 수잔 모두가 찰스를 좋아하고(찰스 쪽으로 가는 화살표 세 개) 찰스는 수잔 한 사람만 좋아함(찰스에게서 나가는 유일한 화살표)을 알 수 있다.

그런 의미에서 찰스는 중요한 사람이고 수잔은 어떻게 보면 찰스를 움직일 수 있는 유일한 사람으로 정치판이라면 숨은 실력자인 셈이다. 그렇다면 이 4명의 영향력 순서를 매길 수 있을까?

이들 네 사람의 역학관계를 표로 나타내면 다음과 같다. 이 표는 4×4 행렬로 표현할 수 있는데 이 행렬을 H라고 부른다. 톰은 자신이 가진 영향력을 셋으로 나눠서 메리, 찰스, 수잔에게 각각 1/3씩 주고 있으며 메리는 자신의 영향력 전체인 1을 찰스에게 주고 있다. 찰스 역시 자신의 영향력 전체인 1을 수잔에게 주고 있고 수잔은 톰과 찰스에게
1/2씩 주고 있다.

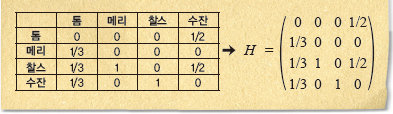
이 행렬로부터 네 사람의 영향력 크기를 비교할 수 있다. 이들의 영향력은 4차원(4개의 원소로 이뤄진) 벡터 v=(a, b, c, d)로 표현할 수 있는데 각 영향력의 합, 즉 전체 영향력을 1로 놓는다(a+b+c+ d=1). 톰의 영향력 a는 톰이 다른 사람들로부터 받는 영향력의 합으로 이 경우 수잔 영향력의 1/2이다. 즉 a=d/2. 메리의 영향력 b는 톰 영향력의
1/3로 b=a/3이다. 찰스의 영향력 c는 톰 영향력의 1/3, 메리의 전부, 수잔의 1/2을 합친 값(c=a/3+b+d/2)이다. 끝으로 수잔은 톰의 1/3과 찰스의 전부를 합친 값이다(d=a/3+c).

결국 이런 관계는 행렬 H와 벡터 v의 곱인 4차원 벡터로 표시할 수 있다. 결국 행렬 H와 벡터 v의 곱이 벡터 v와 동일한 벡터 v의 원소를 구하면 각각의 영향력을 알 수 있다(Hv=v). 위의 경우를 풀면 네 사람의 영향력 비율은 다음과 같다. 즉 숨은 실력자 수잔이 찰스보다도 영향력이 큼을 알 수 있다.

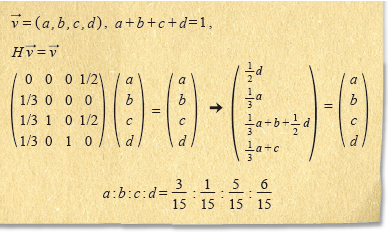
이제 원래 문제로 돌아가 각자 자기가 원하는 사람에게 돈을 어떻게 줄 것인지 마음먹고 있던 상태를 100×100 행렬 H라고 적으면 각 사람들의 중요도는 차원이 100인 벡터 v로 쓸 수 있고 Hv=v 라고 놓은 뒤 v를 구한다. 즉 벡터 v의 원소(차원)값이 큰 순서대로 검색등수가 정해지는 셈이다. 방정식 Hv=v의 해 v를 고유벡터라고 부르는데, 훨씬 차원이 큰 행렬에서 고유벡터를 빠르게 찾는 문제는 응용수학에서 많이 연구하는 분야다.

100000×100000 행렬 정도는 수학과 대학원 학생도 흔히 다룬다.
마지막으로 이 방정식의 의미는 어떤 사람이 인터넷에서 링크만을 따라 한가롭게 서핑을 한다면 결국 사이트의 중요도가 큰 곳으로 가게 된다는 의미다. 결국 구글이나 네이버로 가게 된다. 모든 길은 로마로 향하듯. 1

행렬(行列)
수 또는 문자를 직사각형 모양으로 배열해 괄호로 묶은 것을 행렬이라고 한다. 가로 줄을 행(行)이라 하고, 세로 줄을 열(列)이라 한다. 행의 수가 m개이고, 열의 수가 n개인 행렬을 mxn 행렬이라고 한다.
벡터(vector)
크기와 방향을 가진 양으로 기호 위에 화살표를 붙인다. 행의 수가 1개이고, 열의 수가 n개인 1xn 행렬은 n차원 벡터라고 볼 수 있다. 예를 들어 (1, 5, 6)은 3차원 벡터다.

한상근 교수는 미국 오하이오주립대에서 박사학위를 받고 1989년 KAIST에 부임했다. 정수론과 그 응용인 암호학, 정보학 분야를 연구하고 있다. 1992년 조선시대 수학자 최석정의 저서 ‘구수략’을 접하고 이듬해 ‘최석정과 그의 마방진’이라는 논문을 써 최석정이 조합론 분야의 원조임을 알리는 데 기여했다.