“연세대 전기전자공학부 송홍엽 교수의 노력으로 마침내 최석정의 업적이 해외 학계에서 공인됐습니다. ‘Handbook of Combinatorial Designs’라는 책에 최석정이 나왔습니다. 인터넷에서 책의 원문을 보여주고 있습니다. 12페이지에 나옵니다. 최석정의 업적이 역사적인 관점에서 매우 훌륭하게 소개됐다고 생각합니다.”
지난 6월 2일 오전, 기자는 KAIST 수학과 한상근 교수가 전날 저녁 흥분이 가시지 않은 상태에서 쓴 것으로 보이는 e메일을 읽었다. ‘무슨 얘기지…?’한 교수가 알려준 사이트에 들어가 책을 보니 정말 12페이지에 아래와 같은 글이 있었다.
The literature on latin squares goes back at least 300 years to the monograph Koo-Soo-Ryak by Choi Seok-Jeong (1646-1715); he uses orthogonal latin squares of order 9 to construct a magic square and notes that he cannot find orthogonal latin squares of order 10.
라틴방진을 다룬 문헌은 적어도 300년 전 최석정(1646-1715)의 ‘구수략’까지 거슬러 올라간다. 그는 마방진을 만들려고 9차 직교라틴방진을 이용했고 10차 직교라틴방진을 만드는 데는 실패했다고 적었다.
이날 오후 기자는 연세대 송 교수의 연구실 문을 두드렸다.
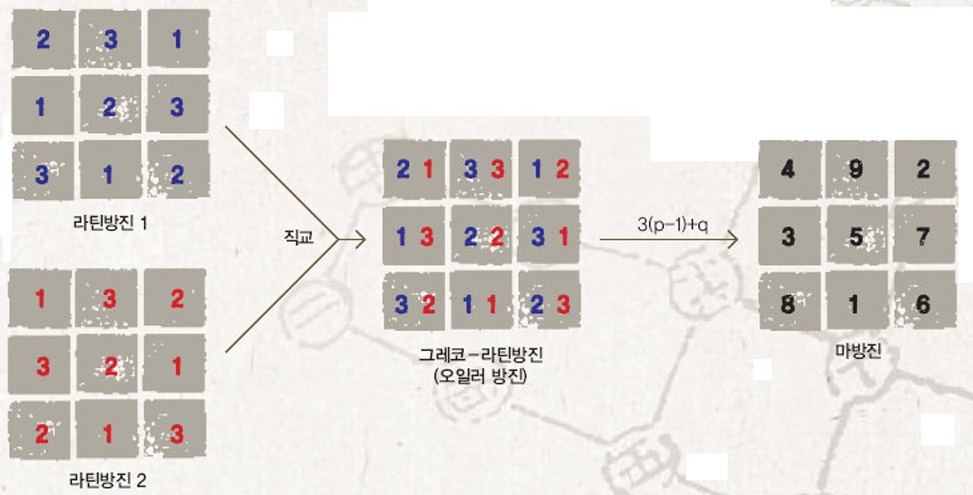
두 개의 라틴방진을 겹쳐 놓았을 때 각 항목이 서로 다른‘그레코-라틴방진’이 얻어지면 이들을 교라틴방진이라고 부른다. 3차 그레코-라틴방진(가운데)의 경우 각 성분의 첫째 수 p에서 1을 빼고 3을 곱한 뒤 둘째 수 q를 더한 값을 지닌 배열을 만들면 3차 마방진(오른쪽)이 된다.
조합론의 원조 직교라틴방진
“책을 펴서 최석정이 소개된 부분을 확인하니 뿌듯하더군요. 너무 짤막해서 아쉽기는 했습니다만….”
송 교수는 지난해 초 있었던 일을 뒤늦게 얘기하기가 쑥스럽다면서도 마치 어제 일인 듯 설명하기 시작했다. 최석정은 조선시대 영의정까지 지냈던 인물로 아마추어 수학자였다. 그의 저서 ‘구수략’(九數略)은 조선시대 최고의 수학책으로 꼽힌다.
최석정과 그의 ‘구수략’이 소개돼 있다며 송 교수가 보여준 두꺼운 책의 표지에는 ‘Handbook of Combinatorial Designs’(조합론 디자인 편람)이라는 제목이 써 있다. 조합론 디자인이란 순열이나 조합처럼 주어진 대상에서 특정한 조건을 충족시키는 경우의 수가 몇 가지인지 그리고 그들 사이에는 어떤 구조가 숨어있는지 알아내는 방법을 연구하는 수학의 한 분야다.
이 편람은 조합론 디자인의 세부 주제를 각 전공자들이 맡아 기술한 글을 묶은 책인데 송 교수도 저자로 참여했다. 송 교수가 연구하는 통신이론은 깊이 파헤치다보면 조합론과 관련된 수학을 다뤄야 한다. 그런데 조합론 디자인과 조선시대 아마추어 수학자 최석정이 무슨 관련이 있을까.
이 편람에서 최석정이 언급된 부분은 조합론 디자인의 역사를 다룬 2장 ‘고대로부터 1 950년대까지’의 맨 앞부분. 저자들은 조합론의 출발점으로 직교라틴방진을 들면서 최석정의 ‘구수략’이 직교라틴방진을 기록한 최초의 문헌이라고 소개했다. 직교라틴방진을 이해하려면 먼저 라틴방진을 알아야한다. 라틴방진은 n개의 서로 다른 숫자(또는 문자나 그림)를 n행 n열(이를 ‘n차’라고 부른다)의 체스판 같은 공간 즉 방진에 배열한 구조다. 물론 조건이 있어 어느 행이나 열에서도 숫자가 한번만 나와야 한다. 조금만 생각하면 작은 차수의 라틴방진은 쉽게 만들 수 있다.
최석정보다 61년 뒤인 1707년 스위스에서 태어난 천재 수학자 레오나드 오일러는 라틴방진을 연구하다 두 가지 라틴방진을 겹쳐놓았을 때 각 항목이 모두 다른 경우를 생각해내고 여기에 ‘그레코-라틴방진’이라는 이름을 붙였다. 하나는 그리스어 알파벳으로, 다른 하나는 라틴어 알파벳으로 이뤄져 있는 두 라틴 방진을 합쳤기 때문인데, 그 뒤 오일러를 기려 그레코-라틴 방진을 ‘오일러 방진’이라고도 부른다. 라틴방진 가운데 서로 쌍을 이뤘을 때 그레코-라틴 방진을 만들 수 있는 경우를 ‘직교라틴방진’이라고 부른다.
직교라틴방진이 조합론 디자인의 원조라고 여겨지는 이유는 효율적인 실험을 위한 실험 디자인에 쓰이기 때문이다. 20세기 초 영국의 통계학자 겸 유전학자인 로날드 피셔는 밀 4종류와 비료 4종류 가운데 토질이 일정치 않은 밭에 재배할 최적의 쌍을 찾는 실험을 할 때 4차 직교라틴방진을 이용했다. 주어진 밭에서 가장 잘 자라는 씨앗과 비료를 가장 적은 실험횟수를 통해 찾는 방법으로 직교라틴방진 쌍으로 이뤄진 그레코-라틴방진의 배열을 택했던 것. 그 뒤 직교라틴방진은 여러 분야의 실험 디자인에 널리 쓰이고 있다. 또한 이동통신시스템에서 전송 신호의 모양이나 채널코드를 설계하는 분야 등의 다양한 공학적인 분야에서도 이용되는데, 이 점이 바로 통신공학자인 송 교수와 직교라틴방진을 이어주는 연결 고리다.

헝가리 노(老) 수학자의 관심에서 비롯
1996년 나온 ‘조합론 디자인 편람’ 초판을 보면 최석정 이야기가 없다. 그런데 10년 뒤 나온 2판에서는 어떤 과정을 거쳐 최석정의 업적이 소개될 수 있었을까. 지금은 고인이 된 헝가리의 수학자 조시아 데니쉬 박사는 1974년 ‘라틴방진과 그 응용’이라는 책을 펴냈는데 1990년대 2판을 계획하고 있었다. 그는 우연히 1993년 국내 학술지에 최석정의 구수략을 다룬 논문이 실렸다는 이야기를 듣고 1997년 독일의 한 학회에서 만난 송홍엽 교수에게 이 논문을 번역해 보내달라고 요청했다. 데니쉬 박사와 송 교수의 미국 유학시절 지도교수가 친한 사이였기 때문에 송 교수와도 안면이 있었던 것.
데니쉬 박사가 요청한 논문은 ‘한국수학교육학회지’에 실린 KAIST 한상근 교수팀의 ‘최석정과 그의 마방진’이라는 제목의 논문이다. 1992년 ‘구수략’의 존재를 알게 된 한 교수는 책에서 9차 직교라틴방진을 발견하고 최석정이 마방진을 만들기 위해 직교라틴방진을 이용했다는 요지의 논문을 발표했다. 마방진은 영어 ‘magic square’를 번역한 용어로 1부터 n2까지 자연수가 n차 방진에 특수하게 배열된 구조다. 즉 모든 행이나 열의 숫자를 합치면 같은 값이 나온다. 최석정은 ‘구수략’에서 다양한 마방진을 소개했다. (최석정과 마방진에 대한 자세한 내용은 과학동아 1999년 7월호 68쪽 ‘수학사의 미스터리 마방진’ 참조)
송 교수는 한 교수의 논문을 영어로 번역해 데니쉬 박사에게 보내줬다. 그런데 데니쉬 박사는 끝내 2판을 내지 못하고 2000년 사망했다. 송 교수는 “아마 데니쉬 박사는 2판에 최석정의 업적을 소개하기 위해 자료를 요청했을 것”이라며 “그의 죽음으로 좋은 기회를 놓친 것 같아 안타까웠다”고 회상했다. 그 뒤 송 교수는 이 일을 잊고 있었다. 그런데 2006년 ‘조합론 디자인 편람’ 2판을 펼 예정이니 이전 논문을 업데이트해달라고 편집진이 요청했다.
“논문을 다듬다가 문득 최석정과 데니쉬 박사가 떠올랐습니다. 편집진에게 수년 전 데니쉬 박사와 교환한 서신과 한 교수 논문의 번역본을 보냈습니다.”
데니쉬 박사는 조합론 분야의 거장이었기 때문에 편집진들도 그가 2판을 내려다 끝내 이루지 못하고 사망했다는 걸 잘 알고 있었다. 따라서 데니쉬 박사가 최석정 이야기를 2판에 소개하려했다는 송 교수 의견이 설득력있게 받아들여진 것. 같은 해 말 출간된 2판은 이듬해 초 송 교수에게 배달됐다.
“그런데 이 친구들이 최석정을 언급하면서 국적을 표시하지 않았더군요. Korea를 쓰면 좋았을 텐데….” 다행히 뒷부분의 연표를 보니 ‘한국의 최석정’이 ‘스위스의 오일러’의 바로 윗줄에 기술돼 있었다. 송 교수는 이 사실을 KAIST 한상근 교수에게 알려준다는 걸 깜빡 잊었다. 당시 전자공학과 업무에 정신이 없었다고. 그러다가 지난 5월 30일 고려대에서 있었던 암호연구회 워크숍에서 한 교수를 만나 이 얘기를 하게 됐던 것.
“한 교수와 연락을 하고 지낸지는 10년이 넘었지만 이날 처음 만났습니다. 제가 수학과에 있지 않다보니 그동안 만날 기회가 없었네요.”
최석정을 통해 서로 알게 된 송 교수와 한 교수는 이날 밤늦도록 술잔을 기울이며 오래된 친구처럼 정겨운 시간을 보냈다고 한다. 다음날 KAIST로 돌아간 한 교수는 저녁에 기자에게 메일을 보냈던 것.
그런데 ‘편람’에서 최석정과 ‘구수략’을 소개하면서 “그는 마방진을 만들려고 9차 직교라틴방진을 이용했고 10차 직교라틴방진을 만드는 데는 실패했다고 적었다”고 한 부분은 무슨 의미일까.

오일러의 추측 보기 좋게 빗나가
앞에서 마방진은 1에서 n2까지 자연수가 n차 방진에 배열된 특수한 경우라고 설명했다. KAIST 수학과 한상근 교수는 “최석정은 마방진을 체계적으로 만드는 방법을 연구하다 직교라틴방진의 개념을 얻은 것 같다”며 “그의 9차 그레코-라틴방진은 3차 그레코-라틴방진 9개가 합쳐진 형태”라고 설명했다. 그렇다면 그레코-라틴방진에서 어떻게 마방진을 만들 수 있을까.
한 교수는 “각 성분의 첫째 수 p에서 1을 빼고 9를 곱한 뒤 둘째 수 q를 더한 즉 ‘9(p-1)+q’의 값을 가진 배열은 9차 마방진이 된다”며 “최석정도 이 정도는 알고 있었을 것”이라고 말했다. 그렇다면 최석정은 10차 마방진을 만들기 위해 10차 직교라틴방진을 만들려고 했다는 얘기. 그런데 그는 왜 10차 직교라틴방진을 만드는 데는 실패했을까.
라틴방진은 모든 차수에 걸쳐 존재하지만 직교라틴방진은 존재하지 않는 차수가 있다. 가장 간단한 경우는 2차일 때. 2차 방진은 경우의 수가 많지 않기 때문에 직교라틴방진 쌍이 없음을 쉽게 알 수 있다. 최석정이 죽고 수십 년이 지나 지구 저편 유럽에서 라틴방진을 연구했던 오일러는 차수에 따른 직교라틴방진의 존재여부에 대한 흥미로운 패턴을 발견했다. 즉 ‘4k+2’(k는 자연수)차 직교라틴방진을 찾을 수 없었던 것. 최석정이 만들다 실패한 10차 직교라틴방진은 k=2일 때. 오일러는 k=1일 때 즉 6차 직교라틴방진을 찾는 유명한 ‘36장교 문제’ 풀이를 시도했지만 해답을 얻지 못했다. 이를 토대로 그는 ‘4k+2’차 직교라틴방진이 존재하지 않을 것이라는 유명한 ‘오일러의 추측’을 논문으로 발표했다. 그래서 직교라틴방진에 대한 원조 수학자로 오일러를 꼽으며, 직교라틴방진에 대한 연구를 조합론의 효시로 꼽는다.
6개의 부대에서 계급이 다른 장교 6명(예를 들어 소위에서 대령까지 1명씩) 총 36명을 가로 세로 6줄로 세워서, 어떤 줄에서도 6명 모두가 부대와 계급이 다르게 배치할 수 있는가?
금방 답을 찾을 것 같지만 해보면 안 됨을 알 수 있다. 6차 직교라틴방진에 대한 오일러의 추측은 1901년 수학자 가스톤 태리가 모든 가능한 경우를 다 조사한 뒤 옳음이 증명됐다. 그러나 1959년 파커 등은 k=2인 10차 직교라틴방진을 발견했고 그 뒤 14차, 18차 등 k=1일 때를 제외한 모든 경우 오일러 방진이 존재하는 것으로 증명됐다. 천재 수학자의 추측이 보기 좋게 빗나간 셈이다. 만일 최석정이 10차 직교라틴방진을 찾는데 성공했다면 이는 획기적인 업적이 됐을 것이다.
“물론 조합론 분야의 전문가들이 참여해 집필한 책에 최석정의 업적이 실렸다는 사실은 이 분야에서 그의 업적을 ‘인정’했다는 의미이지만 아직 ‘공인’됐다고는 생각하지 않습니다. 누군가가 나서서 ‘구수략’ 영문판을 내고 그 내용과 의미를 요약한 논문을 국제 학술지에 게재해야 비로소 학계에서 공식적으로 인정되는 것이죠.”
송 교수는 수학과에 몸담고 있지 않은 자신이 이 일까지 하기에는 벅차다고 토로했다. KAIST 한상근 교수도 “이제 수학의 역사에 관심이 있는 사람이 나서 이 일을 완결지었으면 좋겠다”고 덧붙였다. 그레코-라틴방진이 또 다른 별칭인 ‘최석정 방진’로 불릴 날을 기대해 본다. 최석정의 ‘구수략’ 한글판은 한국학술진흥재단의 지원으로 2006년 출간됐다.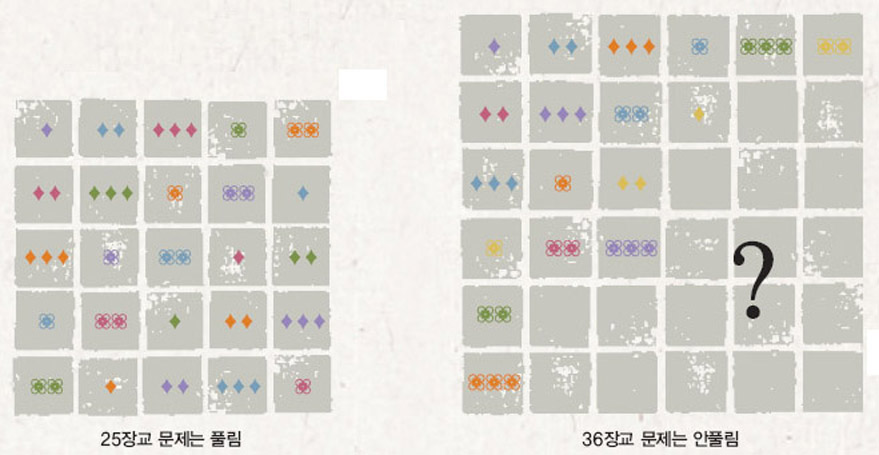
오일러는 6차 직교라틴방진이 없음을 부대와 계급이 서로 다른 장교 배치 문제로 설명했다. 5개 부대(색)에서 계급이 다른 장교 5명 총 25명을 가로 세로 5줄로 세워서 어떤 줄에서도 부대와 계급이 다르게 배치할 수 있지만(왼쪽) 6개 부대에서 계급이 다른 장교 6명 총 36명은 이렇게 배치할 수 없다(오른쪽).