d라이브러리

Q

어느 극장에서 연말을 맞아 커플을 위한 이벤트를 열었다. 커플 100쌍에게는 선착순으로 영화 티켓을 5000원으로 대폭 할인해준 것. 그런데 매표소에서 너무 바쁜 나머지 미처 거스름돈을 준비하지 못한 채 100쌍의 커플을 맞이했다. 이들 중 절반은 5000원짜리를, 나머지 절반은 1만원짜리를 냈는데 신기하게도 거스름돈 때문에 곤란을 겪지 않고 매표가 끝났다. 1만원짜리를 낸 커플에게는 다른 커플이 내고 간 5000원짜리를 거슬러주면 됐기 때문이다. 이런 일이 가능한 확률은 얼마일까?

A

1887년 프랑스 수학자 조셉 베르트랑은 극장 손님에게 거스름돈을 주는 대신 개표 상황으로 이런 문제를 냈다. 주어진 문제를 일반적인 형태로 표현하면, 같은 개수의 +1과 -1을 늘어놓았을 때 차례대로 구한 부분합이 항상 0보다 크거나 같아지는 경우의 수를 구하라는 것이다.

그래프를 이용해 이 문제를 풀어보자. 아래 그래프 (a)는 +1, -1, -1, +1, +1, … 순으로 나열한 합을 나타냈다. +1의 개수를 n이라고 하면 +1과 -1을 나열하는 전체 경우의 수는 ${}_{2n}{C}_{n}$이다. 여기서 부분합이 0보다 작아지는 경우의 수를 빼면 원하는 결과를 얻을 수 있다.
 

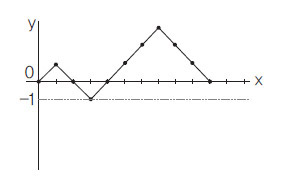
부분합이 0보다 작아진다는 것은 그래프가 y=-1과 만난다는 뜻이다. 처음으로 만나는 점을 찾아서 그 왼쪽 부분을 y=-1에 대해 대칭시키면 그래프 (b)가 된다. 이는 녹색 격자의 한 점에서 다른 점까지 가는 경로의 수를 구하는 문제와 같다. 출발점은 항상 (0, -2)고, 도착점은 (2n, 0)이다. 조합을 이용하면 ${}_{2n}{C}_{n+1}$수식 답임을 알 수 있다. 따라서 구하는 확률은 $1-\frac{{}{2n}{C}{n}+1}{{}{2n}{C}{n}}=\frac{1}{n+1}$이 된다. 참고로 $\frac{{}{2n}{C}{n}}{n+1}$수식은 조합론에서 자주 나오는 수로 ‘카탈란 수’(Catalan number)라는 이름이 붙어있다.
 

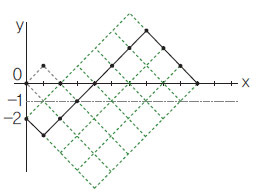
이 기가 막힌 방법은 ‘반전법’(reflection method)이라고 부르는데, 지금까지 프랑스 수학자 디세르 앙드레가 1887년 처음 고안한 것으로 알려졌다. 그런데 올해 수학자 마르크 르노가 쓴 논문에 따르면 앙드레가 이 문제를 공식적으로 푼 첫 번째 인물이긴 하지만 그의 풀이가 반전법과 똑같지는 않다고 한다. 그러니까 ‘앙드레의 반전법’이 정확한 표현은 아니다. 후대에 ‘이 문제는 앙드레가 처음으로 풀었다’와 ‘이 문제는 반전법으로 풀린다’는 말이 합쳐져 ‘이 문제는 앙드레가 반전법으로 멋지게 풀었다’는 오해가 생긴 것일 터.