Q
작년 수학능력시험 언어영역에서 2개의 보기가 정답으로 인정돼 큰 문제가 됐다. 언어영역의 특성상 어쩔 수 없는 일이었지만, 만약 수학에서 잘못된 문제가 출제됐다면 얼마나 큰일이 일어났을까? 다행히 우리나라에서는 아직 그런 경우가 없었지만, 미국판 수능시험이라 할 SAT에서는 모범답안이 틀려 소동이 벌어진 적이 있었다. 바로 다음 문제였다.
3각뿔과 4각뿔이 주어져 있는데, 4각뿔의 밑면을 제외한 모든 면은 똑같은 크기의 정3각형이다. 3각뿔의 한 옆면과 4각뿔의 한 옆면을 정확히 일치하게 붙인다면, 그 결과는 몇개의 면을 가진 입체도형이 될까?
A
원래 SAT 수학 문제가 중학교 수준이기는 하지만, 그렇다고 해도 이 문제는 너무 쉬워 보인다. 3각뿔의 면이 4개, 4각뿔의 면이 5개이고, 2면이 맞붙으니까 4+5-2=7에서 7면체가 답이 될 수밖에. SAT를 주관하는 미국 ETS의 모범답안도 이것이었다.
그러나 뜻밖에도 이것은 정답이 아니었다. 올바른 답은 5면체, 즉 두 도형을 맞붙이면 다섯개의 면이 생기는 것이다.
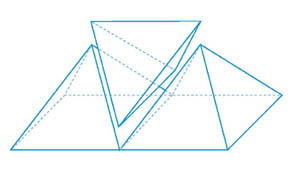
삼각함수를 써서 복잡하게 계산할 수도 있지만, 다음과 같은 방법으로 간단하게 5면체가 된다는 것을 확인할 수 있다. 우선 문제의 4각뿔 2개를 나란히 놓고, 그 사이에 문제의 3각뿔을 끼워 넣는다고 생각해보자.
4각뿔의 옆면이 모두 똑같은 정3각형이므로 3각뿔은 두 4각뿔 사이에 딱 맞게 들어가, 세 입체도형의 옆면은 하나의 면을 이룸을 알 수 있다. 그러니까 처음에 7면체의 답을 구할 때는 맞붙는 2면만 없어지는 것으로 생각했는데, 실제로는 두 입체 도형의 면이 평평하게 만나 하나의 면을 이루는 것이다.
이 문제를 옳게 풀었던 데이비드 로웬(David Lowen)은 모범답안이 틀렸다는 것을 언론에 제보했고, 결국 ETS는 24만명의 점수를 올려줘야 했다.

















