경주 안압지에서 출토된 주사위는 보통 우리가 보아 온 6면체가 아닌 14면으로 된 특이한 것이다. 통일신라 시대(7-9세기)의 유물인 이 주사위는 6개의 정사각면과 8개의 정삼각면을 가지고 있다. 주사위의 각면에는 임의청가(任意請歌, 임의대로 노래 청하기), 삼잔일거(三盞一去, 석 잔을 한 번에 보내기), 금성작무(禁聲作舞, 소리내지 않고 춤추기), 음진대소(飮盡大笑, 다 마시고 크게 웃기) 등 술자리 놀이와 관계된 모두 14개의 한자어구들이 음각돼 있다. 6면 주사위에 비해 훨씬 많은 경우들이 나타났으리라는 것은 쉽게 예측할 수 있다.
14면 주사위의 가치는 술자리 놀이에만 있는 것이 아니다. 확률세계로의 길잡이로도 훌륭하다. 정육면체 주사위의 경우는 던지거나 굴리거나 어떻게 하더라도 각 면의 확률은 너무 뻔하게도 이다. 왜냐하면 각 면이 기하학적으로 완전히 같기 때문이다. 그러나 14면 주사위에서는 정사각면과 정삼각면이 서로 맞물려 있다. 따라서 사각면과 삼각면이 땅에 닿을 확률은 서로 같다고 할 수 없다. 같지 않다면 무엇에 따라 달라지는 것일까.
4각면 확률이 높은 이유
확률을 개념적으로 분류하는 방식에는 여러 가지가 있는데 여기서는 논리적 확률과 통계적 확률로 구분하고자 한다. 논리적 확률은 몇 가지 전제로부터 수리적으로 연역된다. 이에 반해 통계적 확률은 자연 또는 실험상태에서 수집된 관측으로부터 산출된다. 이렇게 상반돼 보이는 두 확률이 어떻게 관련돼 있는지 알아보자.
우선 14면 주사위의 논리적 확률을 생각해 보자. 위로 던져진 14면 주사위가 떨어지면서 바닥에 닿는 순간을 보자. 이 때 주사위가 바닥에 접하는 즉시 그대로 달라붙을 만큼 바닥면이 끈끈하다고 가정하자.
이 때 바닥면과 정반대인 위쪽에는 동일한 형태의 면이 관측된다. 이런 경우에 삼각면이 땅에 닿을 확률은 그 삼각면에 의해 지탱되고 있는 외접구(球) 상의 삼각형의 표면적에 비례한다. 마찬가지로 사각면이 닿을 확률은 사각면에 의해 지탱되고 있는 구사각형의 표면적에 비례한다.
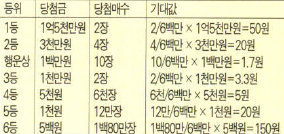
14면 주사위를 던졌을 때 삼각면이 땅에 닿을 확률은 외접구의 총 표면적에서 해당 구삼각형이 차지하고 있는 표면적이 된다. 이것을 구면기하학의 한 공식을 써서 구해보면 (3 cos-1( ) - π) / 4π = 0.0439이고 총 삼각면의 확률은 이것의 8배인 0.3510이 된다. 한편 총 사각면의 확률은 0.6490이다. 즉 14면 주사위를 던졌을 때 사각면이 바닥에 닿을 확률이 삼각면이 닿을 확률보다 훨씬 높음을 알 수 있다.
굴리는 게 유리해
주사위의 운동을 주의깊게 살펴보면 바닥 면에 충돌한 주사위는 구른다는 것을 발견할 수 있다. 가끔 주사위로 놀이를 할 때면 주사위를 굴리는 사람들도 볼 수 있다. 주사위를 굴리는 것이 과연 어떤 이득을 가져다 줄까. 그냥 던질 때와 달리 확률이 어떻게 되길래 굴리는 것일까.
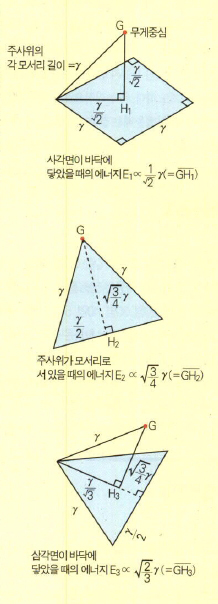
구르는 주사위가 겪게 되는 과정을 에너지로 설명해 보자. 주사위는 사각면을 바닥에 깔고 있을 때 가장 낮은 수준의 위치에너지 E1을 갖는다. 반면 그것을 약간 움직여 모서리를 바닥에 대고 올곧이 서있게 하기 위해서는 가장 큰 위치에너지 E2가 필요하다. 그러므로 그 차이인 E2-E1 만큼은 주사위가 구르면서 소모된다.
이제 모서리를 대고 있던 주사위가 삼각면 쪽으로 넘어가는 과정을 살펴보자. 완전히 넘어가 삼각면을 바닥에 대는 순간의 위치에너지를 E3라고 하면, 그 때의 주사위 높이는 사각면이 바닥이었을 때보다 높으므로 에너지는 E1 <; E3 <; E2 임을 알 수 있다. 그런데 이 때 주사위가 얻게 되는 위치에너지의 변화량은 주사위가 바닥면에 닿는 순간 충돌로 완전히 소실된다고 가정하자. 즉 그런 정도로 물렁물렁한 바닥면을 전제하자는 것이다. 그리고 주사위가 삼각면 바닥에서 다시 모서리에 서기 위해서는 E2-E3 만큼의 에너지를 소모해야 한다. 모서리에 선 주사위는 다시 사각면 쪽으로 넘어가게 되는데 이때도 역시 주사위가 획득하는 에너지는 바닥면 충돌 때 소멸되는 것으로 하자. 그러므로 굴려진 14면 주사위는 사각면, 모서리, 삼각면, 모서리, …의 과정을 겪으면서 E2-E1, E2-E3, …만큼씩 초기 에너지를 손실해가면서 이것이 0이 되는 순간 정지하게 될 것이다.
따라서 사각면과 삼각면의 출현확률은 E2-E1:E2-E3에 비례한다. 기하학적 방법을 동원해 계산하면 총 사각면의 확률은 0.7624, 총 삼각면의 확률로 0.2376이다. 따라서 주사위를 굴렸을 때가 주사위를 위로 던졌을 때에 비해 사각면이 나올 확률이 커진다는 것을 알 수 있다. 이런 것이 14면 주사위의 논리적 확률이다.
경험으로 얻어진 통계적 확률
그렇다면 통계적 확률은 무엇일까. 필자는 14면 주사위의 통계적 확률을 구하기 위해 수년 전 정확한 14면 주사위를 제작해(실제 14면 주사위에서는 삼각면이 더 깊게 파여 있다) 며칠 밤에 걸쳐 이불을 깔고 실험을 해봤다. 그 결과는 다음과 같았다. 주사위를 위로 1천번 던졌을 때 사각면이 6백57번 출현했다. 즉 총 사각면의 통계적 확률은 0.657이고 통계적 오차까지 허용하면 0.657 ± 0.030 (95% 신뢰수준에서)이다.
한편 주사위를 옆으로 굴렸을 때는 사각면이 2천회 시행에서 1천5백19번 출현했다. 즉 총 사각면의 통계적 확률은 0.760이고 통계적 오차까지 허용하면 0.760 ± 0.019 (95% 신뢰수준에서)이다. 그 결과를 논리적 확률과 비교해 보면 위로 던졌을 때는 통계적 확률이 약간 크게 나왔고 옆으로 던졌을 때는 비슷하게 나왔다. 위로 던져진 주사위의 경우가 이불에 착지한 후 실제로는 약간씩 구르기도 하기 때문으로 생각된다.
이렇듯 통계적 확률은 논리적 확률과 다를 수도 있고 거의 비슷할 수도 있다. 결과적으로 다르다면 논리적 사고의 틀(과학적 모형)이 현실과 부합하지 않음을 뜻한다. 반면 두 확률이 비슷하다면 논리적 사고의 틀이 현실과 부합하는 것을 뜻하므로 통계적 확률은 과학적 모형을 검증하는 역할을 한다. 이렇듯 논리적 확률과 통계적 확률은 각기 개념은 상이하지만 역할면에서는 서로 보완적이다.