d라이브러리

지질작용으로 인해 태초의 암석은 대부분 사라지고 없다. 그러나 만일 태초의 암석이 발견된다면 지구의 나이는 물론 새로운 정보도 쉽게 밝혀질 것이다.

우리가 살고 있는 지구의 나이는 얼마나 될까. 이런 질문은 하나님께 무례한 짓으로 여기던 18세기 이전부터 계속돼 왔다. 그렇지만 아직도 이 질문에 과학적 정답을 줄 사람은 아무도 없다. 하나의 가설로서 지구는 45억년 전에 태양에서 분리된 행성이란 추측이 있을 뿐이다.

인간이 달을 정복한 것은 23년 전의 일이다. 달에서 가져온 암석을 분석한 결과 달의 나이가 45억7천만년으로 측정됐다. 이 자료는 지구의 나이를 추정하는 데 참고가 된다.

그동안 지구암석 가운데 가장 오랜 암석은 남 그린랜드의 편마암으로 밝혀졌는데, 연령은 37억년으로 측정됐다. 한반도에서는 경기 육괴(경기-서울지역에 분포하는 편마암류의 지층)의 한 편마암이 가장 오랜 암석으로 추정되며, 지금까지 측정된 자료에 의하면 27억년 전에 형성된 것으로 보인다.

지구의 표면은 계속 변한다. 깎이고, 내려앉고, 그리고 솟아나는 지질작용으로 인해 태초의 암석은 대부분 사라지고 없다. 만일 태초의 암석이 발견된다면 지구의 나이는 물론 새로운 정보도 쉽게 밝혀질 것이다. 지질작용은 지질시대에 살던 생물의 유해와 흔적을 묻어 놓았는데, 지금까지 남아 있는 것을 화석이라 한다.

암석연령 알 수 있는 방사성동위원소
 

지질시대와는 관계 없이 종족이 계속 이어져 온 생물이 있는가 하면, 어떤 생물은 한 시대에 원인 모르게 멸종해 버린 것도 있다. 전자는 시상화석이며 암석의 생성환경을 연구하는데 쓰이고, 후자는 표준화석이며 암석의 연령을 추정하는데 이용된다. 표준화석으로 알게 된 것을 상대연대라 한다.

그렇다면 절대연대란 표현도 가능할 것인가. 물론 가능하다. 방사성동위원소(뒤에 자세히 설명)를 이용하면 암석의 연령을 측정할 수 있다. 동위원소연령이란 바로 그런 방법으로 알게 된 연령이다. 그밖에 화학반응속도를 추정해 연령을 측정한 화학연령도 있다. 이 둘을 합쳐 절대연대라 부른다.

연대측정을 설명하기 전에 우리가 잘 알고 있는 원자의 구조부터 알아보자. 원자는 원자핵(양성자, 중성자, 그리고 중간자로 구성)과 원자핵의 주위를 빠른 속도로 회전하는 전자로 구성돼 있다. 마치 태양계에서 태양을 중심으로 행성들이 일정한 궤도를 회전하는 모양과 비슷하다.

원자핵은 원자의 물리적 성질과 관계되고, 원자의 무게는 원자핵의 질량수(양성자와 중성자의 수를 합친 정도 : 탄소－14 또는 ${}^{14}$C에서 질량수는 14임)로 나타낸다. 그와는 달리 전자는 원자의 화학적 성질과 깊은 관계가 있다.

주기율표는 원자의 화학적 성질이 같은 것들로 그룹을 지어 묶어 둔 것이다. 그 표에서 같은 위치에 놓여지면서 질량수가 다른 원자가 있다는 사실이 확인됐다. 영국의 프레데릭 소디가 그리스어로 '같은 위치'란 뜻을 처음 붙인 것이 지금의 동위원소다.

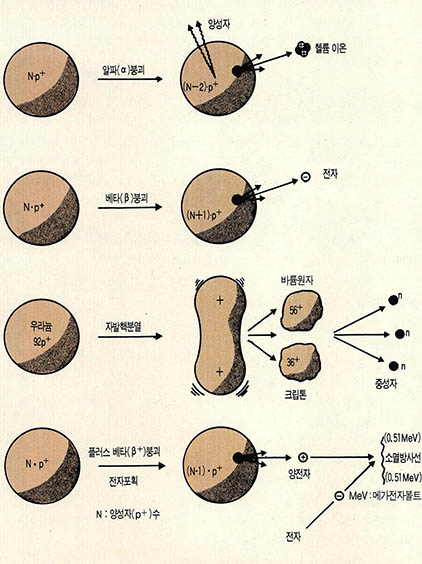
동위원소는 불안정한 원자핵을 가진 것과 안정된 원자핵을 가진 것으로 구별된다. 불안정한 원자핵은 방사선(α,β,γ 그리고 중성자)을 원자핵 밖으로 내보내 안정되려고 한다(그림1). 원자핵이 불안정한 동위원소를 방사성동위원소라 한다. 핵이 안정된 것은 안정동위원소인데, 이는 최근 암석의 생성과정과 그때의 환경을 밝히는 데 매우 중요하다. 원자핵은 일정한 법칙에 따라 붕괴해 방사선을 내보내면서 새로운 동위원소를 만든다(그림2).

1900년 프레데릭 소디에 의해 붕괴법칙이 확립됐다. 붕괴하는 쪽이 어미원소, 만들어지는 쪽이 딸원소다. 어미원소의 무게가 반으로 줄어드는데 걸리는 시간을 반감기라 한다. 반감기와 관계있는 것으로 원자핵이 단위시간에 붕괴할 수 있는 확률을 붕괴율 또는 붕괴상수라 한다. 연령을 계산할 때 바로 이것을 기준으로 삼는다.

어미원소가 반으로 줄면 줄어든 양만큼 새로운 딸원소가 생기는 질량보존법칙은 연대측정에도 적용된다. 연대측정은 어미원소와 딸원소의 질량이나 방사선의 세기를 측정해 서로 비교하는 일이 그 전부다. 예를 들어 모래시계의 원리를 머리 속에 그려 놓으면 알기 쉽다. 이동된 모래의 양을 보고 시간을 짐작할 수 있는 것과 매우 비슷하다.

절대연대의 측정방법들은 여러가지가 있다. 그러나 여기서는 중요한 다섯 가지만 비교해 보기로 하자.

첫째 어미원소와 딸원소의 질량비를 측정해 그들의 비율로 연령을 계산하는 방법, 둘째 우주방사성동위원소의 방사선 세기를 측정해 연령을 얻는 방법, 셋째 우라늄-토륨-프로트악티늄의 비평형에 의한 연대측정법, 넷째 방사선이 물질을 통과할 때 그 물질에 남긴 흠집을 측정해 연령을 얻는 방법, 그리고 다섯째 화학반응으로 생긴 물질의 양을 측정해 연령을 얻는 방법 등이 있다.

마지막 방법은 방사성동위원소를 이용한 것이 아니지만 절대연대를 알 수 있는 또 다른 분야다. 대표적인 방법을 한가지씩 좀더 자세히 알아보자.
 

1. 어미원소와 딸원소의 비율에 의한 방법

많이 이용되는 방법은 루비듐-스트론튬(Rb-Sr)법, 칼륨-아르곤(K-Ar)법, 우라늄-토륨-납(U-Th-Pb)법, 아르곤-아르곤(${}^{39}$Ar-${}^{40}$Ar)법, 그리고 사마륨-네오디뮴(Sm-Nd)법 등이다. 이들은 어미원소의 반감기가 매우 길어서 비교적 오래된(천만년 이상) 암석의 연령을 측정하는데 알맞다.

먼저 Rb-Sr법에 대해서 알아보자. 이 방법은 마그마(암석이 녹은 것)가 굳어서 된 암석의 연령을 측정하는 데 주로 이용된다. 암석은 여러 종류의 원소들로 구성되고 Rb과 Sr원소도 함께 들어 있다. Rb은 ${}^{85}$Rb(존재하는 비율 : 72.1654％)와 ${}^{87}$Rb(27.8346％)이 있다. 그 중에서 ${}^{87}$Rb이 방사성동위원소이며 그의 원자핵은 ${β}^{-}$(마이너스베타)붕괴를 해 딸원소인 ${}^{87}$Sr이 된다. ${}^{87}$Rb의 반감기는 48억8천만년(붕괴상수 : 1.42×${10}^{－11}$/년)이다.

Sr원소에도 4개의 동위원소가 있다. 즉, ${}^{84}$Sr(0.56％), ${}^{86}$Sr(9.86％), ${}^{87}$Sr(7.00％), 그리고 ${}^{88}$Sr(82.58％)이 그것이다.

${}^{87}$Sr는 암석의 종류와 연령에 따라 그 비율이 다르다. 이는 마그마가 굳어질 때 그의 ${}^{87}$Sr의 존재비율이 일정하나 암석이 된 다음부터 지질시대를 경과하는 동안 ${}^{87}$Rb이 붕괴된 ${}^{87}$Sr(방사계 ${}^{87}$Sr)이 점점 쌓이게 되기 때문이다. Rb-Sr법에서는 이 둘을 구별해야 연대측정이 가능하다. 이 둘을 구별하는 방법은 다음과 같다.

같은 마그마에서 굳어진 암석이라도 생길 때의 지질환경에 따라 Rb과 Sr의 분포는 조금씩 다르다. Rb이 많으면 상대적으로 ${}^{87}$Sr의 양도 많이 생긴다. 한 암석에서 Rb의 양이 각각 다른 시료를 선정해 질량 분석기를 이용, ${}^{87}$Sr/${}^{86}$Sr의 비를 측정한다.

${}^{87}$Rb/${}^{86}$Sr의 비는 그 시료의 Rb과 Sr의 함량으로 계산한다. XY좌표에 X축은 ${}^{87}$Rb/${}^{86}$Sr, Y축은 ${}^{87}$Sr/${}^{86}$Sr의 값으로 그래프를 그리면 직선이 나타난다. 그 직선이 아이소크론(isochron)이다.

X축의 값이 0일 때 Y축의 값을 '초기 ${}^{87}$Sr/${}^{86}$Sr 값'이라 부르는데, 이는 마그마를 연구하는 데 중요한 자료가 된다. 그리고 그 직선 기울기의 크기로 암석의 연령이 계산된다. 연령이 오래될수록 기울기의 경사는 시계침의 반대방향으로 올라간다.

2. 우주방사성동위원소의 방사능에 의한 방법

대표적인 방법은 탄소－14(C-14)법, 삼중수소(${}^{3}$H)법, 삼중수소－헬륨(${}^{3}$H-${}^{3}$He)법, 베릴륨－10(Be-10)법, 그리고 망간－54(Mn-54)법 등이다.

위의 어미원소들은 모두 우주선(cosmic ray)으로 만들어진다. 대기권의 공기에 섞인 어떤 원자가 우주선을 쪼이면 그의 원자핵이 파열되면서 새로운 방사성동위원소로 변한다. 이들은 대기권에 머물다가 빗물과 눈에 섞여 지표에 스며든다. 또 식물이 광합성 작용으로 직접 대기의 탄소를 영양소로 합성시켜 생장하며 동물은 이들 식물을 먹고 자라는 먹이사슬 과정에서, 동식물에 들어 오는 경로가 있다. C-14법을 예로 그 원리를 좀더 자세히 알아보자.

탄소는 세 종류의 동위원소가 있다. 즉 ${}^{12}$C(98.89％), ${}^{13}$C(1.11％), 그리고 ${}^{14}$C(${}^{12}$C의 1.2×${10}^{－12}$배)가 그것이다. 셋 중에서 ${}^{14}$C는 거의 무시할 수 있는 적은 양이지만 연대측정의 수단으로 쓰인다.

${}^{14}$C는 공기에 있던 질소－14가 우주선의 중성자와 핵반응(중성자가 ${}^{14}$N의 핵을 때리면 그의 핵이 파괴되면서 ${}^{14}$C로 되고 나머지 에너지가 양성자로 빠져 나가는 반응 : ${}^{14}$N(n,P)${}^{14}$C)을 해 생긴다. ${}^{14}$C는 ${β}^{-}$의 붕괴(반감기 : 5730±40년)를 한다. ${}^{14}$C는 공기 중의 이산화탄소 또는 ${CO}_{2}$(0.03％ 체적비)에 일정한 비율로 들어 있다. ${}^{14}$C는 탄소사이클에 의해 생체조직의 탄소에 혼합된다.

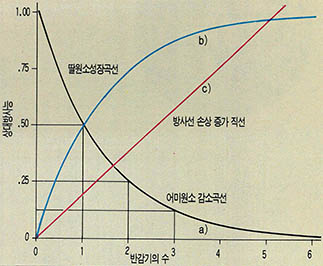
탄소사이클에는 호수나 바닷물에 녹은 탄산기(${CO}_{3}$ ${}^{－}$)가 탄산염으로 침전되는 순환과정과, 지표 위의 동식물과 대기권의 탄소 사이에서 일어나는 순환계가 있다. C-14의 연대측정은 후자의 순환계와 밀접한 관계가 있다. 탄소사이클이 계속되는 동식물(즉 살아있는 생체)의 몸을 구성하는 탄소원자에는 일정한 비율의 ${}^{14}$C가 섞여 있다. 방사선의 세기로 나타내면 13.56±0.07 dpm/gC(dpm은 1분당 붕괴 횟수, gC는 탄소의 g무게)다.

생물이 죽으면 탄소사이클이 중단되고 그 후부터 ${}^{14}$C는 스스로 붕괴해 양이 줄어든다. 살아 있을 때 ${}^{14}$C의 양을 알고 있으므로 줄어든 ${}^{14}$C의 양은 곧 연령으로 계산된다(그림).
 

3. 우라늄-토륨-프로트악티늄의 비평형에 의한 방법

암석과 같은 천연물질에는 연속적으로 원자핵의 붕괴가 이어져 나아가는 세개의 계열이 있다. ${}^{238}$U이 시조인 ${}^{238}$U계열, ${}^{232}$Th이 시조인 ${}^{232}$Th계열, 그리고 ${}^{235}$U가 시조인 악티늄계열 등이 그것이다. 각 계열은 대를 이으면서 붕괴를 계속하다가 ${}^{238}$U은 납－206(${}^{206}$Pb), ${}^{232}$Th은 ${}^{208}$Pb, 그리고 ${}^{235}$U는 ${}^{207}$Pb에 이르게 되면 끝난다. 이러한 연속적 붕괴의 현상을 이용하면 수천년에서 수십만년의 퇴적층 연령을 측정할 수 있다. 그 대표적인 방법은 이오늄-우라늄(${}^{230}$Th-${}^{234}$U)법과 Pb-210 법이 있다.

위의 세 계열은 암석에서 모두 어미원소의 붕괴하는 속도와 딸원소의 생성되는 속도가 일정하게 유지되고 있다. 이런 상태를 방사평형이라 한다. 그와는 반대로 계속 이어지던 연속붕괴에서 중도에 대가 끊어지는 경우가 있다. 그런 상태를 방사비평형 또는 비평형이라 한다. 예컨대 ${}^{238}$U계열이 마지막의 ${}^{206}$Pb으로 되기까지는 14번의 세대교체가 있다. ${}^{238}$U계열에서 시조인 ${}^{238}$U을 제1세대라 할 때 제 4세대인 ${}^{234}$U가 붕괴하면 제 5세대인 ${}^{230}$Th으로 된다. 이 과정에서 비평형이 되는 경우를 살펴보자.

암석과 같이 굳어진 것은 대체로 방사평형이 유지될 수 있지만, 바다나 호수의 경우는 물질이 이동하므로 굳어진 물체와는 다르다. 우라늄은 물에 녹지만 토륨은 그렇지 않다. 물의 ${}^{234}$U가 붕괴해 생긴 ${}^{230}$Th은 해양퇴적물인 제올라이트(zeolite)와 중정석에 섞여 바다밑에 침전되므로 바닷물 속의 ${}^{234}$U와 자연적으로 분리된다. 즉 비평형이 이루어진다.

시조인 ${}^{238}$U계열에서 벗어난 ${}^{230}$Th은 독립해 붕괴한다. 그의 반감기는 7.52×${10}^{4}$년이다. 퇴적층의 두께와 ${}^{230}$Th의 방사선의 세기(방사능)는 반비례한다. 조사된 자료에 의하면 해양퇴적층의 ${}^{230}$Th은 그 대부분이 ${}^{238}$U계열에서 생긴 것이고 25％ 정도가 ${}^{232}$Th계열에서 발생된 것으로 알려지고 있다.

비평형에 의한 연대측정은 불가능하던 퇴적층의 정확한 퇴적속도의 측정, 퇴적물의 이동 메커니즘의 규명, 그리고 고(古)해안선 등을 추적할 수 있는 유일한 수단으로 쓰인다.

원자력발전소 같은 국가의 기간산업시설을 건설할 때에는 지각의 안정성이 과거 3만년 이전에도 변화가 있었는지 주변 암석의 연령을 측정해야 한다. 이런 수단은 뒤에 설명하는 화학연령과 함께 매우 효과적이다.

4. 방사선의 손상에 의한 방법

방사선이 물질에 닿으면 그 물질에 어떤 흠집을 남긴다. 그런 흠집은 연대측정뿐만 아니라 방사선의 계측에도 많이 이용된다. 흠집을 이용한 연대측정의 대표적인 방법은 피션트랙(fisson track:FT)법, 열형광(TL)법, 그리고 전자스핀공명(ESR)법 등이 있다.

두가지 형태의 흠집이 연령측정에 이용된다. 방사선에 의해 물질의 기본조직 단위인 결정격자가 파괴된 피션트랙과 방사선이 물질과의 상호작용으로 그 물질원자의 전자를 그의 궤도에서 얼마동안 벗어나게 잡아둠으로써 결정구조에 결함을 주는 전자각현상으로 나눈다. 궤도를 벗어난 전자는 외부에서 열을 가하면 형광 빛을 내면서 정상 궤도에 진입한다. 앞의 피션트랙과 뒤의 전자각현상은 각각 FT법과 TL법의 기초가 된다. FT법에 대해서 좀 더 자세히 알아보자.

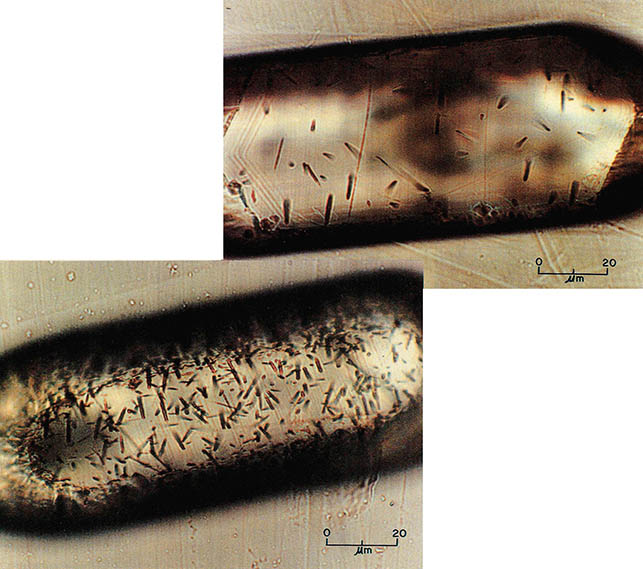
광물에 기록된 피션트랙은 앞에서 설명한 세 계열의 자발핵분열로 생긴 방사선(주로 알파입자의 에너지)에 의한 것이므로 자발피션트랙이라 한다(그림4). 알파입자는 질량이 무겁기 때문에 고체에서 수십μm밖에 날지 못한다. 그러나 그의 높은 에너지 때문에 지나간 곳에 흠집으로 트랙을 남긴다. 현미경으로 그 트랙을 볼 수 있다. 광물 1㎠ 면적에는 수백내지 수만개의 트랙이 있다. 광물에서 관찰되는 트랙은 주로 광물에 있던 ${}^{238}$U의 자발핵분열에서 만들어진 것으로 알려지고 있다.

${}^{235}$U핵이 쪼개져도 트랙이 생긴다. 광물을 원자로 속에 넣고 열중성자(속도가 느린 중성자)를 쪼이면 ${}^{235}$U의 원자핵이 분열해 트랙을 만든다. 자발피션트랙과 구별하기 위해 이것을 유도피션트랙이라 한다. 피션트랙은 표면밀도(트랙스/㎠)로 표시한다. 아직 학자들 사이에 자발피션트랙을 만드는 우라늄의 붕괴상수가 일치된 것은 없지만 4가지 상수가 알려지고 있다. 그중에서 8.57×${10}^{－17}$/이 최근 값이다.

유도피션트랙의 표면밀도는 원자로의 열중성자 밀도(중성자수/㎠)와 쪼일 물질의 놓이는 위치에 따라 영향을 받는다. 원자로 속의 열중성자 밀도는 ±10％에서 변한다고 실험에 의해 알려지고 있다. 연령과 피션트랙의 표면밀도가 잘 알려진 표준모니터(주로 백운모와 인공유리)를 이용하면 열중성자를 쪼일 때의 불확실한 조건들을 포함, 붕괴상수를 동시에 보정할 수 있다. 이런 방식을 제타(zeta)보정이라 한다.

암석은 광물로 구성되고 광물에는 일정량의 우라늄이 들어 있다. 우라늄이 만든 자발피션트랙의 표면밀도는 우라늄의 양과 경과한 시간에 비례한다. 천연우라늄은 일정 비율의 ${}^{235}$U가 포함돼 있으므로 유도피션트랙의 표면밀도는 단지 우라늄의 양에만 의존한다. 따라서 자발피션트랙의 표면밀도와 유도피션트랙의 표면밀도 비는 곧 그 암석의 연령으로 계산할 수 있다.
 

5. 화학반응률에 의한 방법

마지막으로 화학반응을 이용한 연대측정방법을 알아보자. 대표적인 것은 아미노산-라세미아반응(amino-acid-racemization:AAR)법이다. 원리는 화학반응률을 먼저 가정한 다음 새로 생긴 화학물질의 양을 측정해 그 비율에 따라 연령을 얻을 수 있다. 최근에 이 분야의 연구가 활발하다. 그 이유는 상대적으로 손쉽고, 신속하고, 값싼 방법이기 때문이다. 이는 특히 인류학자, 고생물학자, 그리고 고지형학자 등이 선호하는 방법이다. AAR법을 간략하게 소개한다.

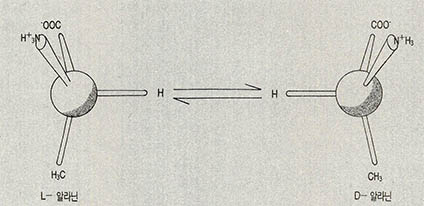
화석 속의 해골에는 10여가지 아미노산이 있다. 아미노산의 구조는 탄소원자를 축으로 한 쪽은 수소, 다른 쪽은 4~5개의 분자그룹이 서로 비대칭으로 마주보고 있다. 분자그룹이 놓이는 위치가 서로 다른 아미노산의 이성체가 연대측정의 수단이 된다.

분자그룹이 놓여 있는 위치가 왼쪽(left:L)이면 L-아미노산, 오른쪽(dextro:D)이면 D-아미노산이란 명칭을 붙인다. 생물체가 살아있을 때 D-아미노산은 없고 L-아미노산만 있다. 그와는 반대로 생물체가 죽게 되면 죽은 시간의 길이에 비례해 D-아미노산이 많아진다. 이것을 라세미아 반응이라 한다. 연령은 D-아미노산/L-아미노산의 비로서 계산한다.

연대측정의 대상이 생물체의 유해를 선정한다는 점은 앞에서 설명한 C-14법의 경우와 비슷하나 전자는 방사성동위원소의 붕괴원리에, 후자는 화학물질의 반응률에, 기초를 두고 있어서 매우 흥미롭다.

과학은 생동하는 생명체와 같은 속성이 있다. 또 다른 새로운 연대측정 이론이 개발돼 의문으로 남아 있는 지구의 나이를 과학적으로 밝힐 수 있기를 기대해 본다.