d라이브러리

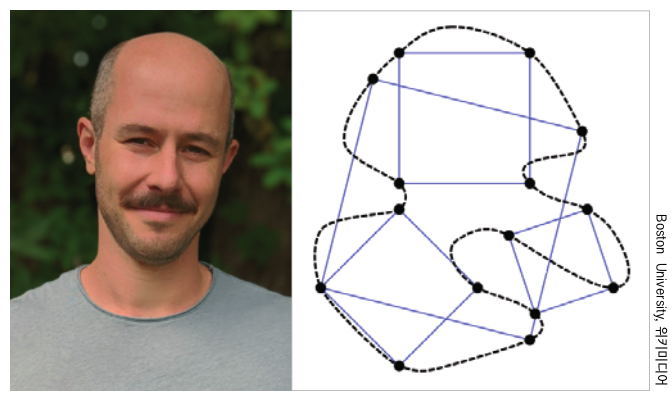
조슈아 그린(사진) 미국 보스턴대학교 수학과 교수와 앤드루 롭 영국 더럼대학교 수학과 교수가 100년 넘게 풀리지 않았던 난제의 해법을 제시했습니다. 두 사람은 코로나19로 만나기가 어려워지자 영상통화를 하며 문제를 풀었습니다.

두 수학자가 주목한 난제는 1911년 독일 수학자 오토 퇴플리츠가 처음 제기한 ‘내접 사각형 문제’입니다. 조르당 곡선 위의 점들로 항상 정사각형을 만들 수 있는지 밝히는 문제로  ‘퇴플리츠 문제’라고도 불리죠. 조르당 곡선은 시작점과 끝점이 같으면서 중간에 교차하지 않는 연속한 곡선입니다.

정사각형이 아닌 직사각형을 만드는 문제는 1981년 미국 수학자 도로시 본이 해결했습니다. 이후 수학자들은 특정 비율이 되는 직사각형이 있는지 증명하는 데 도전했죠. 그러던 2018년 미국 프린스턴대학교의 대학원생 콜 휴젤마이어가 가로세로 비율이 인 직사각형이 항상 존재한다는 것을 증명했습니다. 두 교수는 휴젤마이어와 본의 생각을 발전시켜 조르당 곡선 위에는 임의의 가로세로 비율을 갖는 직사각형이 반드시 존재한다는 것을 확인했습니다. 이 증명이 맞다면 가로세로 비율이 1인 정사각형이 존재하는 것도 저절로 증명되죠. 이 연구 결과는 5월 19일 온라인 논문 발표 사이트 ‘아카이브’에 올라왔습니다.