그리스의 수학자 에우클레이데스(유클리드)가 ‘기하학 원론’이라는 평면 기하 교과서를 쓴 지 1700여 년이 지났습니다. 하지만 아직도 미해결인 평면 기하 문제가 많습니다. 이번 호에 소개할 문제 역시 그중 하나입니다. 1950년 대학에 갓 입학한 새내기가 만든 문제로, 최근 영국의 생물학자인 아마추어 수학자가 이 문제에 관해 의미 있는 결과를 발표했습니다.

평면의 각 점에 색을 칠하는데, 거리가 정확히 1 떨어진 점은 다른 색이 되게 칠하려고 합니다. 색이 최소 몇 개 필요할까요?
이 같은 규칙으로 칠할 때 필요한 최소 색의 수를 ‘평면 채색수(χ)’라고 합시다. 이 값을 구하는 문제는 사실 누가 처음으로 냈는지가 기록마다 달라 혼란이 있었습니다. 1990년대 미국 수학자 알레산더 소이퍼 교수가 이 문제에 관한 글을 쓴 사람을 일일이 연락해 추적한 끝에 출제자를 밝혀냈지요.
바로 1950년 당시 만 18세로 미국 시카고대학교 수학과에 갓 입학한 에드워드 넬슨이었습니다. 뛰어난 학생이었던 넬슨은 3년만에 석사, 2년 만에 박사 학위를 받고, 1959년에 미국 프린스턴대학교 수학과 교수가 됩니다.
한편 평면 채색수는 항상 3 이상입니다. 어떻게 알 수 있을까요? 한 변의 길이가 1인 정삼각형을 그려봅시다. 그러면 정삼각형의 세 꼭짓점은 서로 다른 색이 돼야 하므로 3색 이상이 필요합니다.
4 이상일 수는 없을까요? 넬슨은 곧바로 이게 참이라는 걸 알아냅니다. 정삼각형 4개를 겹쳐서 아래와 같은 그림을 만듭시다. 이때 점 D와 점 G의 거리는 1입니다. 그러면 각 변은 모두 길이가 1인 선분입니다. 이제 χ≥4임을 증명하기 위해 이 그림에 있는 점을 모두 3색으로 칠할 수 있다고 가정 합시다.
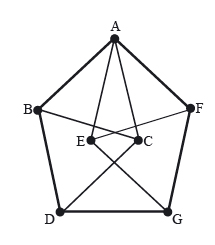
△ABC는 한 변의 길이가 1인 정삼각형이므로, 각 꼭짓점의 색은 다릅니다. 마찬가지로 △BCD의 모든 꼭짓점도 색이 다른데요, 칠할 수 있는 색이 3개 밖에 없다고 가정했기 때문에 점 A와 점 D의 색은 같아야 합니다.
같은 방법으로 △AEF와 △EFG의 꼭짓점을 칠합니다. 정삼각형을 이루고 있는 꼭짓점의 색은 모두 다르고 3색으로만 칠하다 보니 어쩔 수 없이 점 D와 점 G의 색이 같아집니다. 그런데 앞서서 두 점 사이의 거리는 1이라고 했기 때문에 모순이 생기고 맙니다. 결국 4색은 돼야 하지요.
에르되시도 인정한 좋은 문제
이제까지 색의 수가 너무 적으면 절대 칠할 수 없다는 부정적인 결과만 소개했습니다. 반대로 색이 충분히 많으면 무조건 된다는 긍정적인 결과에는 어떤 것이 있었을까요?
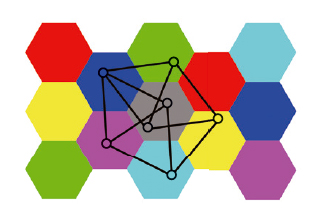
넬슨의 대학 선배인 미국 수학자 존 이즈벨은 넬슨이 χ≥4만 증명했다는 소리를 듣고, 궁리해 χ≤7임을 보였습니다. 사실 7색으로 칠하는 방법에는 여러 가지가 있습니다. 그중 가장 많이 알려진 건 정육각형으로 평면을 가득 채우는 방법에서 착안한 겁니다.
정육각형의 한 변의 길이를 잘 정해 위 그림처럼 같은 색으로 된 두 정육각형은 서로 거리가 1보다 크게 하고, 정육각형 안에는 거리가 1 떨어진 두 점이 없도록 만들면 됩니다.
그렇다면 χ는 4, 5, 6, 7 중 얼마일까요? 정말 많은 수학자와 공동연구하며 여러 문제를 섭렵했던 헝가리 수학자 에르되시 팔도 이 문제에 도전했습니다. 1992년 강연 도중 이 문제를 언급하면서, 아주 좋은 문제고 내가 만든 문제라면 250달러 정도를 상금으로 걸었을 것이라고 말하기도 했습니다. 에르되시는 자기가 낸 문제마다 난이도에 따라 1달러부터 5000달러까지 상금을 건 것으로 유명하죠.
에르되시는 네덜란드 수학자 니콜라스 더브라윈과 함께 만일 χ>k라면 k개 색으로 칠할 수 없는 유한개의 점이 반드시 있다는 것을 증명했습니다. 무한히 많은 점 때문에 어려운 문제로 보이지만, 덕분에 평면에서 유한개의 점을 뽑았을 때 몇 가지 색으로 칠할 수 있냐는 유한에 관한 문제로 바꿔서 생각할 수 있게 됐습니다.

1000년 살 수 있다는 생물학자가 문제 해결
그 뒤로 얼마 전까지 이 문제에 관한 진척이 별로 없었습니다. 그러던 2018년 4월 8일, χ≥5라는 것을 증명한 논문이 인터넷에 올라왔습니다. 이 연구를 한 사람은 수학자가 아니라 ‘인간은 1000세까지 살 수 있다’는 다소 과격한 주장을 하는 영국 생물학자인 오브리 드 그레이입니다.
그레이 박사는 4색으로 칠할 수 없는 점 1000여 개를 평면에서 잘 찾아냈습니다. 아까 χ≥4를 증명하기 위해서 3색으로 칠할 수 없는 점 7개를 소개했는데요, χ≥5를 보이기 위해 훨씬 더 많은 점을 사용한 것이지요.
저는 수학자가 한 연구도 아니고 해서 이 논문에 관심을 갖지 않았습니다. 그런데 며칠 뒤 컴퓨터로 연구를 검증했다는 학자들이 여럿 나타났고, 결과가 참이라는 것이 밝혀졌습니다.

보통 수학 논문을 검증하는 데 꽤나 긴 시간이 걸립니다. 그런데 이 문제의 경우 오래 걸리지 않았습니다. 논문에서 이야기하는 점을 어떻게 뽑은 것인지만 알면 컴퓨터를 써서 바로 확인할 수 있기 때문입니다. 그레이 박사의 논문에는 1581개의 점을 뽑아내는 방법이 나와 있고, 왜 4가지 색으로 칠할 수 없는지 알아낸 방법이 나옵니다.
한편 4월 14일부터 폴리매스 프로젝트를 통해 여러 사람이 4색으로 칠할 수 없는 점의 최소 개수를 찾고 있습니다. 그레이 박사가 만든 그래프를 조금 더 간단한 것으로 계속 바꿔나가면서 계산하고 있는데, 현재 최고 기록은 5월 6일 미국 텍사스대학교 오스틴캠퍼스 소속의 마레인 횔러 박사가 공개한 633개입니다.
χ는 과연 얼마일까요? 5, 6, 7? 과연 또 누가 이 문제로 사람들을 깜짝 놀라게 할지 궁금합니다. 누구든 도전하면 아무도 생각하지 못한 아이디어로 χ<7이나 χ>5를 증명할 수 있지 않을까요?
엄상일 교수는 KAIST 수학과를 졸업하고, 미국 프린스턴대학교에서 박사 학위를 받았습니다. 현재는 KAIST에서 강의와 연구를 하고 있습니다. 그래프이론과 이산수학, 조합적 최적화가 주요 연구 분야입니다. 2012년에는 젊은과학자상(대통령상)을 수상했고, 2017년에는 한국차세대과학기술한림원 회원으로 선정됐습니다.
















