한 내각의 크기가 108°인 정오각형으로는 평면을 채울 수 없습니다. 108°는 360°의 약수가 아니기 때문이지요. 대신 모서리를 당기고 눌러서 만든 볼록 오각형(어떤 내각의 크기도 180°를 넘지 않는 오각형)은 가능합니다. 그렇다면 몇 가지가 가능할까요?
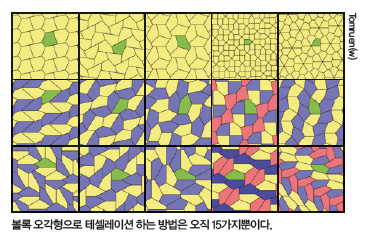
최근 미카엘 라오 프랑스 국립과학연구소 연구원은 그 방법이 15가지뿐이라는 사실을 밝혔습니다. 라오 박사는 4가지 조건 아래 볼록 오각형이 평면 위에서 빈틈없이 맞닿는 모든 경우의 수를 조사했습니다.
4가지 조건은 모든 내각의 합은 540°일 것, 내각은 모두 테셀레이션 무늬를 이룰 것, 한 꼭짓점에서 만나는 모든 내각의 합이 360°일 것, 다른 볼록 오각형의 모서리에 꼭짓점이 올 경우 이 꼭짓점에 모인 내각의 합이 180°일 것입니다.
그 결과 총 371가지 경우의 수가 나왔습니다. 그리고 어떤 경우든 이미 밝혀진 15가지 방법 중 하나에 속한다는 것을 컴퓨터로 밝혔지요. 1918년 독일 수학자 칼 라인하르트가 최초로 5가지 방법을 찾은 이래 2015년까지 총 15가지 방법이 알려져 있었거든요. 이제 더 이상 볼록 오각형 테셀레이션의 새로운 방법을 찾겠다고 매달릴 필요가 없겠죠?

















