
GIB
계산을 빨리 할 수 있는 컴퓨터가 등장하면서 난수도 더 빨리 만들 수 있게 됐다. 난수 만드는 데 컴퓨터를 쓴 최초의 인물은 바로 헝가리 출신의 미국수학자 존 폰 노이만이었다.노이만은 유체에 작용하는 힘을 계산하기 위한 ‘몬테카를로 시뮬레이션’을 만들었다. 몬테카를로 시뮬레이션은 확률분포로 우연한 결과를 나타내주는 방법이다. 예측할 수 없는 불확실한 상황을 미리 실험할 때 사용한다. 따라서 시뮬레이션에는 규칙이 없는, 예측할 수 없는 무작위 수가 필요했다.

제곱으로 만드는 난수
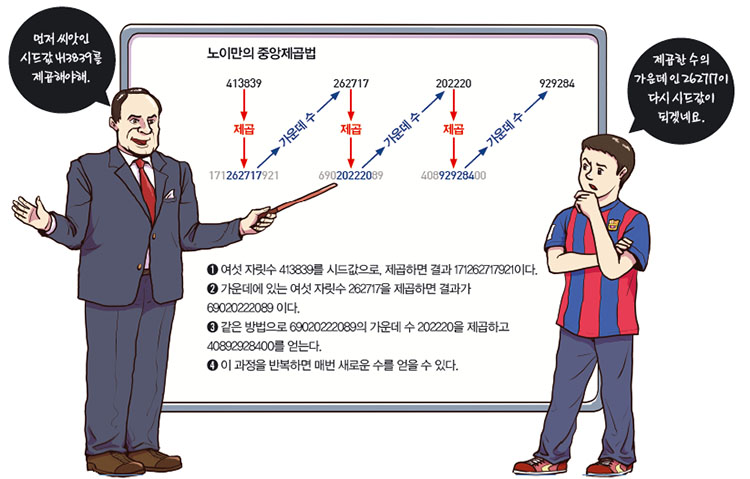
폰 노이만은 무작위 수를 만들어 내기 위한 알고리즘을 만들어냈다. ‘중앙제곱법’이라는 이름의 이 알고리즘은 컴퓨터를 이용해 난수를 만드는 첫 번째 방법이었다. 중앙제곱법은 13세기 프란체스코회 수도회 문서에도 등장했지만, 공식적으로 발표된 건 1949년 폰 노이만에 의해서였다. 중앙제곱법은 ‘시드(seed)’라고 부르는 임의의 수를 제곱한 뒤, 나온 수의 가운데 일부분을 제곱해가며 난수를 만드는 방식이다.
열매를 맺으려면 씨앗을 심어야 한다. 마찬가지로 컴퓨터로 난수를 만들려면 씨앗, 시드값을 입력해야 한다. 씨앗은 어떻게 생겼고, 씨앗을 넣으면 어떤 열매가 나올까? 노이만은 씨앗이 되는 수인 시드값을 제곱한 뒤 양 끝에서 숫자 몇 개를 떼어내고 남은 수를 제곱하는 방식을 썼다.

다른 씨앗을 심으면 다른 열매가 나오듯이, 다른 시드값을 넣으면 만들어지는 난수도 바뀐다. 물론 시드값이 달라도 같은 난수가 생길 수 있지만 확률이 낮아 충분히 무작위의 숫자라고 볼 수 있다.

이 방법에는 단점이 있다. 경우에 따라서는 같은수가 계속 반복될 수도 있고, 가운데 수가 0이 되는 경우에는 더 이상 난수를 만들어내지 못한다. 폰 노이만의 난수 생성법은 시드가 n자리 수일 때 난수가 반복되는 주기가 8n보다 항상 짧거나 어떤 숫자로 수렴한다.
이처럼 컴퓨터 알고리즘으로 만들어 내는 난수를 ‘의사난수’라고 한다. 사람이 보기에는 어느 정도 무작위해 보여 난수로 취급하지만, 정해진 알고리즘으로 만들기 때문에 진짜 난수는 아니다. 그래서 ‘난수를 흉내낸 것’ 또는 ‘가짜 난수’라는 의미로 의사난수라고 한다. 즉 폰 노이만의 방법도 예측 가능하다는 점에서 진정한 난수가 아니다.
게임 아이템은 선형합동법에 물어보세요
오늘날 컴퓨터 프로그램에 가장 많이 사용하는 ‘선형합동법’은 수열과 합동을 이용한다. 수열은 자연수를 이용해 두 개 이상의 항의 관계를 나타낸 식을 뜻한다. 그리고 어떤 수로 나눴을 때 나머지가 같은 수를 합동이라고 한다. 예를 들어 13과 25는 12로 나누었을 때 모두 나머지가 1이어서 12에 대해 합동이다. 수식으로는 13≡25(mod 12)이다.
폰 노이만의 방법과 마찬가지로 이 알고리즘에도 씨앗이 필요하다. 씨앗에 따라 알고리즘이 만들어 내는 숫자의 주기가 달라진다. 주기는 무작위로 나열되는 숫자의 개수가 얼마나 많은지를 나타낸다. 알고리즘에 있는 a와 m, 그리고 시드값이 클수록 주기가 길어진다. 주기가 길어질수록 무작위성이 강하다고 볼 수 있다.
이 알고리즘은 주기가 있고, 주기에 따라서 숫자 나열이 반복된다는 것이 단점이다. 그럼에도 이 알고리즘을 많이 쓰는 데는 이유가 있다. 씨앗으로 사용하는 숫자가 어느 정도 크면 사람은 물론 컴퓨터도 규칙을 찾는 게 불가능해진다. 즉 난수로 봐도 무방한 것이다. 난수 생성 주기가 약 230이면 230개의 숫자는 무작위로 나타난다는 것이다. 230개, 적어도 10억 개의 숫자가 나타난 뒤 반복되는 것이니, 난수로 쓸 만하지 않을까?
이 알고리즘은 단점이 있지만 계산 속도가 충분히 빨라서 정교한 수준의 난수가 필요하지 않는 분야에서 많이 쓰인다. 현재 컴퓨터 프로그램에는 대부분 이 알고리즘을 이용한다. 게임에서 무작위로 캐릭터나 아이템을 뽑는 데도 이 알고리즘이 숨어있다.

게임 아이템은 선형합동법에 물어보세요
오늘날 컴퓨터 프로그램에 가장 많이 사용하는 ‘선형합동법’은 수열과 합동을 이용한다. 수열은 자연수를 이용해 두 개 이상의 항의 관계를 나타낸 식을 뜻한다. 그리고 어떤 수로 나눴을 때 나머지가 같은 수를 합동이라고 한다. 예를 들어 13과 25는 12로 나누었을 때 모두 나머지가 1이어서 12에 대해 합동이다. 수식으로는 13≡25(mod 12)이다.
폰 노이만의 방법과 마찬가지로 이 알고리즘에도 씨앗이 필요하다. 씨앗에 따라 알고리즘이 만들어 내는 숫자의 주기가 달라진다. 주기는 무작위로 나열되는 숫자의 개수가 얼마나 많은지를 나타낸다. 알고리즘에 있는 a와 m, 그리고 시드값이 클수록 주기가 길어진다. 주기가 길어질수록 무작위성이 강하다고 볼 수 있다.
이 알고리즘은 주기가 있고, 주기에 따라서 숫자 나열이 반복된다는 것이 단점이다. 그럼에도 이 알고리즘을 많이 쓰는 데는 이유가 있다. 씨앗으로 사용하는 숫자가 어느 정도 크면 사람은 물론 컴퓨터도 규칙을 찾는 게 불가능해진다. 즉 난수로 봐도 무방한 것이다. 난수 생성 주기가 약 230이면 230개의 숫자는 무작위로 나타난다는 것이다. 230개, 적어도 10억 개의 숫자가 나타난 뒤 반복되는 것이니, 난수로 쓸 만하지 않을까?
이 알고리즘은 단점이 있지만 계산 속도가 충분히 빨라서 정교한 수준의 난수가 필요하지 않는 분야에서 많이 쓰인다. 현재 컴퓨터 프로그램에는 대부분 이 알고리즘을 이용한다. 게임에서 무작위로 캐릭터나 아이템을 뽑는 데도 이 알고리즘이 숨어있다.

소수를 이용한 생성기, 메르센 트위스터

1997년 마츠모토 마코토와 니시무라 다쿠지는 ‘메르센 트위스터’라는 난수생성기를 만들었다. 메르센 소수는 프랑스의 수학자 메르센이 만든 수다. 메르센은 2의 거듭제곱에서 1이 모자란 수에 메르센 수라는 이름을 붙였고, 그중에 소수인 수를 특히 메르센 소수라고 했다.
메르센 트위스터는 난수의 반복 주기가 메르센 소수인 데서 유래했다. 메르센 트위스터는 기존의 난수생성기보다 주기가 훨씬 더 길며 속도도 빠르다. 주기는 219937-1로 이 수는 현재 49개로 알려진 메르센 소수 중 24번째 수다.
선형합동법과 비교하면 메르센 트위스터가 훨씬 더 정교한 난수생성기라는 것을 알 수 있다. 하지만 메르센 트위스터도 결국 주기가 있기 때문에 궁극적으로 완벽한 난수생성기라고는 볼 수 없다. 현재 가장 똑똑한 컴퓨터로도 주기가 없는 난수를 만들 수 없다면 정말 완전한 난수는 만들 수 없는 것일까?

▼관련기사를 계속 보시려면?
Intro. 난수
Part1. 난수, 넌 누구니?
Part 2. 난수의 컴퓨터 시대
Part 3. 완벽한 난수를 찾아서
참고자료 : <;역사 속에 숨겨진 코드 암호 이야기>;











