퍼즐캠프 안내문
축하합니다! 이 안내문은 퍼즐캠프 참가자에게만 발송되었습니다. 다시 말해, 지금 이 안내문을 읽고 있는 여러분은 무사히 사과를 꺼내서 퍼즐캠프에 참가할 수 있는 자격을 얻었단 얘기죠. 그런데 잠깐! 퍼즐캠프를 제대로 즐기려면 퍼즐의 대가들에 대한 이해는 기본이겠지요? 아래 4명의 퍼즐가들 중에는 직접 캠프에 찾아오시는 분들도 있으니 꼼꼼히 읽어 두세요!
수학과 퍼즐의 기막힌 만남 마틴 가드너 1914~2010
수학과 퍼즐이 만나 천생연분이 되었다면 그 인연의 중심에는 아마 마틴 가드너가 있을 것이다. 그만큼 그는 퍼즐에 수학을 접목시켜 많은 사람들에게 즐거움을 주고 있는 ‘유희수학’ 분야의 대표적 인물이다.
마틴 가드너가 유명세를 타게 된 계기는 미국의 저명한 과학잡지인 ‘사이언티픽 아메리칸’에 쓴 하나의 칼럼 덕분이었다. 그는 1956년 사이언티픽 아메리칸 12월호에 ‘플렉사곤(flexagon)’에 대해 소개하는 글을 썼다. 플렉사곤은 아래 그림처럼 종이를 접어 만드는 일종의 장난감으로, 휘어진다는 뜻의 ‘flex’와 다각형을 의미하는 ‘gon’의 합성어다. 사실 플렉사곤은 1939년에 영국의 아더 스톤이 무심코 자르다가 남게 된 종이로 처음 만들었다. 당시엔 큰 인기를 얻지 못했지만, 마틴 가드너의 칼럼에 실리면서 선풍적인 인기를 끌었다.
첫 칼럼이 큰 인기를 끈 덕분에 마틴 가드너는 계속 칼럼을 연재할 수 있는 기회를 얻게 된다. 이후 ‘수학게임’이라는 제목으로 그의 칼럼은 1981년까지 무려 25년간 이어졌다. 그는 수시로 수학퍼즐에 관한 책도 집필했는데, 그 수가 무려 70권이 넘는다.
이쯤 되면 마틴 가드너의 수학 실력이 궁금해진다. 놀랍게도 그는 고등학교까지만 정규과정의 수학을 배웠다. 대학에서는 수학과 동떨어져 보이는 철학을 전공했다. 하지만 그는 수학에 대한 남다른 관심으로 수학퍼즐을 연구하고 소개하는 일에 몰두했다. 특히 19세기 말 전 안타깝게도 마틴 가드너는 2010년에 세상을 떠났지만, 고스란히 남은 그의 수학 퍼즐들은 마틴 가드너가 유희수학 분야에 엄청난 공헌을 했음을 알려 주고 있다. 이에 그의 세계적으로 퍼즐 열풍을 일으켰지만 잊혀져 가던 샘 로이드와 헨리 듀드니의 퍼즐을 재조명하면서, 여느 수학자 못지 않은 왕성한 활동을 보였다. 이뿐만 아니라 그는 루이스 캐럴의 소설 <;이상한 나라의 앨리스>;와 속편 <;거울 나라의 앨리스>;를 수학적으로 풀어 쓴 <;주석달린 앨리스>;를 펴내 수학자들을 놀라게 하기도 했다.
안타깝게도 마틴 가드너는 2010년에 세상을 떠났지만, 고스란히 남은 그의 수학 퍼즐들은 마틴 가드너가 유희수학 분야에 엄청난 공헌을 했음을 알려 주고 있다. 이에 그의 팬들은 정기적으로 모여 새로운 퍼즐 아이디어를 공유하는 G4G(Gathering for gardner)라는 이름의 모임도 만들었다.
혹시 나보다 퍼즐 많이 만든 사람 있어?! 샘 로이드 1841~1911
평생 1만 개의 퍼즐을 풀기도 어려운데, 그만큼의 퍼즐을 만든 사람이 있다. 19세기 말 전세계를 퍼즐 열풍으로 빠지게 했던 샘 로이드다.
처음에 그는 체스를 통해 퍼즐의 세계로 빠져들었다. 14살의 나이에 만든 체스 퍼즐은 뉴욕의 한 신문에 게재되기도 했는데, 체스판에 각각 놓인 3개의 말을 가지고 4번만에 체크메이트를 외쳐야 하는 퍼즐이었다. 실제로도 당시 그는 체스 실력이 뛰어나 세계랭킹 15위까지 오르기도 했다.
퍼즐의 소재를 넓혀 수학퍼즐을 만들기 시작한 샘 로이드는 17세에 그의 이름을 전국적으로 알리게 된 당나귀 퍼즐을 선보인다. 종이를 잘라 기수를 말 위에 올바르게 위치시키는 이 퍼즐은 불티나게 팔려 샘 로이드에게 1만 달러라는 큰 돈을 안겨 주었다. 이후 그는 주요 신문과 잡지에 직접 만든 퍼즐을 소개했고, 자연스럽게 ‘퍼즐왕’이라는 별명이 붙었다.
19세기 퍼즐계의 양대산맥 헨리 듀드니 1857~1930
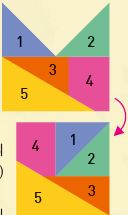
축구계에 호날두와 메시가 있다면, 퍼즐계에는 헨리 듀드니와 샘 로이드가 있다고 할 수 있다. 그만큼 이 두 명은 퍼즐가로서 뛰어났지만 때로는 치열했다. 오른쪽에 나온 주교관 모양의 퍼즐(퍼즐을 조각내 정사각형으로 만드는 퍼즐)의 해답을 두고 샘 로이드와 헨리 듀드니가 벌인 설전은 유명하다. 결과적으로 헨리 듀드니의 승리(오른쪽 그림)로 마무리 됐는데, 그의 뛰어난 수학실력 덕분이었다.
샘 로이드가 정교한 스토리텔링으로 퍼즐의 흥미를 유발했다면, 헨리 듀드니는 퍼즐에 엄밀한 수학적 내용과 지식을 담았다. 하지만 헨리 듀드니 또한 정식으로 수학을 배우지는 않았다. 공무원으로 대부분의 일생을 보낸 헨리 듀드니는 마틴 가드너와 마찬가지로 칼럼을 계기로 자신의 이름을 알렸다. 주로 미스터리를 소재로 삼았던 당시 최고의 인기 잡지인 스트랜드(Strand)지에 꾸준히 퍼즐을 소개했다.
1924년 7월호에 실린 복면산 ‘SEND + MORE = MONEY’는 헨리 듀드니의 대표적인 퍼즐이다. 적은 원고료를 인상해 달라는 뜻에서 이 퍼즐을 만들었다는 이야기도 있다.
동양 퍼즐가의 자존심 노부유키 요시가하라 1936~2004
세계 곳곳의 퍼즐가들은 매년 자신이 직접 발명한 퍼즐을 들고 한데 모인다. 바로 세계퍼즐디자인대회에 참석하기 위해서다. 이 대회에서는 퍼즐가들이 서로의 퍼즐을 풀어보면서 새로운 아이디어를 공유하고 그 해 최고의 퍼즐을 뽑는다. 그런데 이 대회의 명칭이 2005년부터 ‘노부유키 요시가하라 퍼즐 디자인대회’로 변경되었다. 바로 2004년에 세상을 떠난 노부유키 요시가하라의 업적을 기리기 위해서다.
노부유키 요시가하라는 실제 손을 써서 하는 기계적 퍼즐의 대가로 알려져 있다. 자동차 모형의 위치를 하나씩 움직여가며 꽉 막힌 주차장을 탈출하는 ‘러시아워’ 게임이 대표작이다. 노부유키 요시가하라는 대학교에서 화학을 전공했지만, 후에 고등학교에서 학생들에게 수학을 가르치면서 본격적으로 퍼즐에 빠져들게 된다. 그는 80권 이상의 퍼즐과 관련된 책을 썼으며, 수학 퍼즐을 풀기 위한 컴퓨터 프로그램을 짜는 데도 공을 들였다.
STAGE 1 샘 로이드의 숫자퍼즐 강의
안녕하세요? 퍼즐캠프의 시작을 맡은 샘 로이드입니다. 혹시 15퍼즐에 대해 들어보셨나요? 15퍼즐은 4×4칸에 1부터 15까지의 숫자를 차례대로 놓은 뒤, 마지막 14와 15를 바꾸었을 때 다시 원래대로 돌릴 수 있는지를 묻는 퍼즐입니다. 저는 이 퍼즐을 소개하면서 처음으로 푸는 사람에게 1000달러를 상금으로 주겠다고 밝혔어요. 하지만 아무도 풀지 못했죠. 애초부터 이 퍼즐을 푸는 건 수학적으로 불가능하니까요! 이런 게 바로 숫자퍼즐의 묘미가 아닐까요?
“각각 6개의 부대와 계급이 있다. 각 부대에서 계급당 1명씩 36명을 뽑아 6명씩 6줄로 세운다고 할 때, 각 열과 행에 부대와 계급이 겹치지 않게 할 수 있을까?”
이는 18세기의 수학자 오일러가 제시한 ‘36명 장교 세우기 문제’다. 수학적으로는 6차 직교라틴방진이 존재하는지를 묻는 문제로, 라틴방진은 각 행과 열에 동일한 숫자가 겹치지 않는 방진을 말한다. 이 문제에서는 한 칸에 두 조건을 모두 고려해야 하기 때문에 ‘직교라틴방진’ 또는 ‘오일러방진’으로 부른다.
오일러는 처음 이 문제를 제시하면서 2, 6, 10…차 직교라틴방진은 존재하지 않는다고 말했다. 수학자 가스통 타리 또한 조합 가능한 모든 경우를 보이면서 6차 직교라틴방진은 없다는 오일러의 가설을 뒷받침했다. 하지만 이후 10차 직교라틴방진이 발견되면서 오일러의 가설은 결국 틀린 것으로 밝혀졌다.
이런 라틴방진의 원리를 이용한 숫자 퍼즐이 바로 스도쿠이다. 스도쿠는 9차 라틴방진의 변형으로, 9개로 구성된 행과 열에 숫자를 겹치지 않게 배열하는 것이 목적이다. 일본어로 ‘외로운 숫자’라는 의미의 스도쿠는 의외로 일본이 아닌 프랑스에서 시작됐다. 프랑스의 한 일간지에 처음 등장한 스도쿠는 1979년 미국에서 현재와 같은 작은 정사각형 9개에서도 숫자가 겹쳐지면 안 되는 규칙이 추가돼 재탄생 되었다.
한편, 수학적인 계산을 필요로 하는 변형 스도쿠도 있다. 일본의 수학교사가 2004년에 발명한 ‘켄켄’이라는 수학 퍼즐로, 형태는 직소 스도쿠와 유사하지만 켄켄에는 하나의 규칙이 더 추가된다. 각각의 사각형 구석에 적힌 사칙연산의 규칙을 지켜야 한다는 점이다. 예를 들어, 20×라고 적혀 있으면 사각형 안의 모든 숫자를 곱했을 때 20이 되어야 한다.

별별 스도쿠 총집합
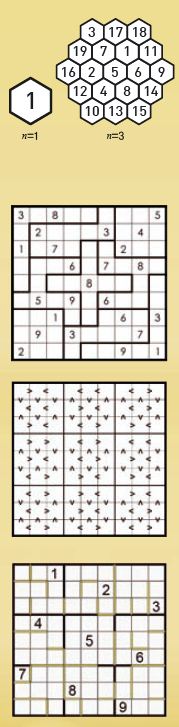
❶ 마법의 6각형
가로, 세로, 대각선으로 더했을 때 항상 같은 숫자가 나오도록 하는 퍼즐이다. 1부터 3n²-3n+1까지 연속되는 자연수를 모두 6각형 틀 안에 배열하는 것이 중요하다. 1887년에 어네스트 본 하셀베르그가 n이 3일때의 ‘마법의 6각형’을 처음 발견한 이후, n이 1인 경우를 제외한 ‘마법의 6각형’은 아직 발견되지 않았다.
❷ 직소 스도쿠
직소 스도쿠는 기존의 3x3의 작은 정사각형 모양이 아닌 직소 모양으로 된 스도쿠이다. 물론 직소 모양에서도 숫자를 한 번씩 사용해야 하는 기본적인 원칙은 지켜야 한다.
❸ 부등호 스도쿠
부등호로 가득 채워진 스도쿠도 있다. 부등호 스도쿠는 배치된 부등호가 성립하도록 숫자를 배열해야 한다. 기본적인 스도쿠의 규칙에 부등호까지 고려해야 하는 어려움이 있다.
❹ 파이프 스도쿠
파이프 스도쿠의 규칙은 더욱 까다롭다. 숫자 사이에 파이프가 있으면, 두 숫자의 차이는 항상 1이어야 한다. 반대로 파이프가 없다면 두 숫자의 차이는 항상 2 이상이어야 한다.
1 첫 번째 퍼즐(샘 로이드 퍼즐)
똑같은 넓이로 땅을 분할하라!
4명의 자식에게 공평하게 땅을 물려 주려고 합니다. 각각의 땅에 한 그루씩 나무가 포함되도록 땅을 4조각으로 분할하세요.
가로, 세로, 대각선으로 더했을 때 항상 같은 숫자가 나오도록 하는 퍼즐이다. 1부터 3n²-3n+1까지 연속되는 자연수를 모두 6각형 틀 안에 배열하는 것이 중요하다. 1887년에 어네스트 본 하셀베르그가 n이 3일때의 ‘마법의 6각형’을 처음 발견한 이후, n이 1인 경우를 제외한 ‘마법의 6각형’은 아직 발견되지 않았다.
❷ 직소 스도쿠
직소 스도쿠는 기존의 3x3의 작은 정사각형 모양이 아닌 직소 모양으로 된 스도쿠이다. 물론 직소 모양에서도 숫자를 한 번씩 사용해야 하는 기본적인 원칙은 지켜야 한다.
❸ 부등호 스도쿠
부등호로 가득 채워진 스도쿠도 있다. 부등호 스도쿠는 배치된 부등호가 성립하도록 숫자를 배열해야 한다. 기본적인 스도쿠의 규칙에 부등호까지 고려해야 하는 어려움이 있다.
❹ 파이프 스도쿠
파이프 스도쿠의 규칙은 더욱 까다롭다. 숫자 사이에 파이프가 있으면, 두 숫자의 차이는 항상 1이어야 한다. 반대로 파이프가 없다면 두 숫자의 차이는 항상 2 이상이어야 한다.
1 첫 번째 퍼즐(샘 로이드 퍼즐)
똑같은 넓이로 땅을 분할하라!
4명의 자식에게 공평하게 땅을 물려 주려고 합니다. 각각의 땅에 한 그루씩 나무가 포함되도록 땅을 4조각으로 분할하세요.
STAGE 2 헨리 듀드니의 문자 퍼즐 강의
SEND + MORE = MONEY. 많이 익숙한 퍼즐이죠? 이 퍼즐의 핵심은 문자에 해당하는 숫자를 알아내는 거예요. 당연히 식도 성립해야 해요. 이런 퍼즐을 ‘복면산’이라고 부르는데, 제가 처음으로 의미까지 있는 복면산을 만들었지요. 그럼 복면산을 비롯한 다양한 문자 퍼즐들을 만나러 가 볼까요?
2004년 구글의 입사시험 첫문제로 나온 복면산 ‘WWWDOT - GOOGLE = DOTCOM’은 많은 지원자들을 당황시켰다. 복면산(覆面算)은 문자나 그림으로 표현된 수식에서 각 문자에 일대일대응하는 숫자를 찾는 퍼즐이다. 마치 숫자가 문자라는 가면을 쓰고 있다는 의미에서 복면산이라는 이름이 붙었다. 예로부터 숫자를 문자로 바꿔서 수식으로 표현한 퍼즐은 다수 존재했지만, 헨리 듀드니는 처음으로 문자에 의미를 부여한 복면산 퍼즐을 만들었다. 그 중 가장 유명한 것이 바로 ‘SEND + MORE = MONEY’이다.
복면산 중에서도 문자로 된 문장 자체가 옳은 식이 되는 걸 ‘이중 성립 복면산’이라고 하는데,이는 1969년에 스티븐 카한이 처음 선보였다. ‘THREE + THREE + TWO + TWO + ONE = ELEVEN’ 등이 이에 해당한다.
복면산을 빨리 풀 수 있는 비법은 없다. 복면산은 모든 숫자를 일일이 대입해가며 답을 찾아야 하는 ‘NP-완전 문제’에 해당하기 때문이다. 다만, 두 글자가 더해져 자리올림이 되었다면 둘 중 하나는 5 이상임을 알 수 있는 정도의 요령은 있다.
박부성 경남대학교 수학교육과 교수는 “복면산에는 논리적인 추론이 자연스럽게 녹아 있다”며, “누구나 퍼즐을 풀어볼 수 있기 때문에 숫자를 다루는 감각을 익히는 데 적합하다”고 복면산의 매력을 설명했다.
본문의 복면산 해답
SEND + MORE = MONEY
▶ 9567 + 1085 = 10652
THREE + THREE + TWO + TWO + ONE = ELEVEN
▶ 84611 + 84611 + 803 + 803 + 391 = 171219
WWWDOT - GOOGLE = DOTCOM
▶ 777589 - 188106 = 589483 또는 777589 - 188103 = 589486
또 다른 문자 퍼즐로는 팬그램(Pangram)이 있다. 팬그램은 모든 문자를 사용하여 하나의 문장을 만드는 퍼즐이다. 한글의 경우 자음과 모음, 영어의 경우 알파벳 전부를 사용한다. 하나씩만 사용하는 것이 원칙이지만, 난이도가 높기 때문에 중복을 허용하기도 한다. 즉, 문장의 길이가 짧을수록 팬그램의 완성도는 높다고 할 수 있다. 팬그램에는 모든 글자가 한 문장 안에 담겨 있기 때문에 서체 확인용 문구로도 종종 사용되고 있다.
The quick brown fox jumps over a lazy dog
▶ 알파벳 a부터 z까지 모두 사용한 팬그램
다람쥐 헌 쳇바퀴에 타고파
▶ 한글의 기본 자음(ㄱ~ㅎ)을 모두 사용한 팬그램
휴가철 전야 도심 교통 큰 불편
▶ 한글의 기본 자음과 모음(ㄱ~ㅎ, ㅏ~ㅣ)를 모두 사용한 팬그램
1877년 크리스마스에는 영국 옥스퍼드대 수학자 루이스 캐럴도 문자를 사용한 퍼즐을 만들었다. ‘더블릿(doublet)’이라는 이름의 이 문자퍼즐은 알파벳을 하나씩 바꿔가면서 처음 단어를 새로운 단어로 바꾸는 퍼즐이다. 가장 적은 단어를 사용해 새로운 단어로 바꾸는 것을 더 좋은 풀이로 본다. 예를 들어 COLD라는 영어단어를 WARM으로 바꾸는 더블릿에는 중간에 총 3개의 단어가 필요하다.

미국의 컴퓨터 과학자이자 수학자인 도널드 커누스 스탠퍼드 대학교 명예교수는 더블릿 풀이에 도움을 주고자, 실생활에서 주로 사용하는 5글자로 된 영어단어 5757개를 골라 분석했다. 그 결과 aloof, earth, sugar 등의 671개 단어는 한 글자만을 바꿔서는 어떠한 영어단어도 되지 않았다. 반대로 한 글자만 바꿔도 더블릿이 성립되는 경우도 103개나 되었다.
2 두 번째 퍼즐
더블릿으로 MATH와 LOVE를 이어라!
MATH와 LOVE를 잇는 가장 짧은 영어단어들을 찾아 주세요.
MATH → LOV E
STAGE 3 고본 후지무라의 기하 퍼즐 강의
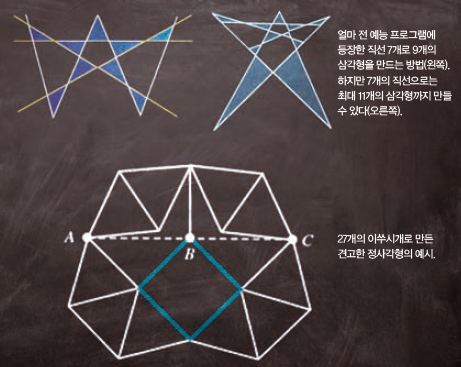
얼마 전 한 예능 프로그램에 제가 만든 퍼즐이 나와서 놀랐습니다. 바로 ‘고본 삼각형’이라는 제 이름을 붙인 기하 퍼즐말입니다. 고본 삼각형이란, 여러 개의 직선으로 겹치지 않는 삼각형을 최대로 많이 만드는 퍼즐입니다. 제가 만든 퍼즐에는 고본 삼각형처럼 기하 퍼즐들이 꽤 있지요. 저와 함께 기하퍼즐의 세계로 들어가 볼까요?
“7개의 직선을 그어 겹치지 않는 삼각형 9개를 만들어라”
고본 삼각형은 얼핏 간단해 보이는 퍼즐이지만, 사실 이 퍼즐은 아직까지 완벽히 풀리지 않은 수학 문제다. 직선 3개로 만들 수 있는 삼각형은 단 하나로, 누구나 쉽게 답을 찾을 수 있다. 하지만 직선의 개수가 늘어날수록 최대로 만들 수 있는 삼각형의 개수를 찾기란 여간 까다로운 일이 아니다. 지금까지 수학자들은 시행착오를 거쳐 직선이 4, 5, 6개일때는 각각 최대 2, 5, 7개의 삼각형을 만들 수 있음을 밝혀냈다.
현재 수학자들은 직선의 수가 많은 경우 나올 수 있는 삼각형의 최댓값을 찾기 위해 연구하고 있다. 2007년 독일의 수학자 요하네스 바더와 프랑스의 수학자 질 클레망은 직선의 개수에 따른 삼각형의 최댓값이 될 수도 있는 값을 구했다(아래 표). 정확히 말하면, 삼각형의 최대 개수를 구한 것이 아니라, 적어도 특정 수 이상은 넘지 않는다는 것을 밝힌 것이다.
그렇다면 앞서 나온 것처럼 7개의 직선으로는 9개의 삼각형을 만드는 것이 최선일까? 이 표에 따르면, 9개가 아닌 11개까지 만들 수 있다. 또한 직선의 개수가 15개일때 최대로 나올 수 있는 삼각형의 개수는 65개다. 2005년 10월, 일본의 토시타카 스즈키는 실제로 65개의 삼각형을 모두 찾아내고 그리는 데 처음으로 성공해 화제가 되기도 했다. 또한 이 표에서는 10개의 직선으로 그릴 수 있는 삼각형의 최대 개수가 26개로 나온다. 그러나 현재까지 25개의 삼각형을 그리는 것까지만 성공했다. 진정한 고본 삼각형 퍼즐의 매력을 느끼고 싶다면, 아직 발견되지 않은 새로운 삼각형을 찾는 데 도전해 보자.
이번에는 정사각형을 만들어 보자. 이쑤시개를 가지고 견고한 정사각형을 만들기 위해서는 최소 몇 개가 필요할까? 여기서 견고한 정사각형이란, 평면 상에서 수학적으로 증명 가능한 완벽한 정사각형을 의미한다. 단순히 4개의 이쑤시개로 정사각형을 만들었다고 해서 수학적으로 완벽한 정사각형이라고 말하는 것은 어렵다.
이 문제는 마틴 가드너가 1963년 사이언티픽 아메리칸 11월호 칼럼에 소개해 화제가 됐다. 마틴 가드너는 미국 버클리대의 수학자 라파엘 로빈슨의 문제를 소개하면서 최소 31개의 이쑤시개가 필요하다고 설명했다. 그런데 2달 뒤, 44명의 독자들이 27개의 이쑤시개로도 견고한 정사각형을 만들 수 있다고 제보했다. 로빈슨의 해답보다 4개나 덜 필요한 셈이다. 이처럼 마틴 가드너는 종종 독자들과의 소통을 통해 더 나은 퍼즐의 해답을 찾기도 했다. 독자들의 의견을 수렴한 마틴 가드너는 이를 수학적으로 증명한 후, 1964년 사이언티픽 아메리칸 2월호에 다시 이 문제를 소개했다.

3 세 번째 퍼즐(고본 후지무라 퍼즐)
최소의 동전을 제거해 정삼각형 모양을 없애라!
크기에 상관없이 정삼각형 형태가 나오지 않으려면 최소 몇 개의 동전을 제거해야 할까요?
보너스 STAGE 바둑알로 즐기는 도미니어링 게임
어느덧 퍼즐캠프도 막바지에 다다르고 있군요. 지금까지 최고의 퍼즐가에게 가장 기본이라고 할 수 있는 숫자, 문자, 기하퍼즐에 대해 알아보았어요. 그럼 마지막으로 저 마틴 가드너와 함께 독특한 퍼즐에 대해 알아보도록 하죠. 먼저 바둑알을 이용한 퍼즐입니다~.
지난 8월 서울에서 열린 세계수학자대회에서는 특별한 강연이 대중들의 이목을 집중시켰다. 바로 두 사람이 바둑알을 가지고 즐기는 이른바 ‘도미니어링(domineering)’ 게임이다. 원래는 도미노를 사용하지만, 이번 세계수학자대회에서는 편의상 바둑알을 사용했다. 이 게임은 서로 번갈아가며 바둑알을 두다가 더 이상 바둑알을 두지 못하는 사람이 지는 것이 기본 규칙이다.
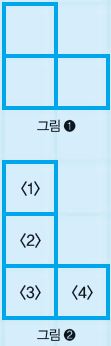
게임의 규칙은 간단하다. 서로 순서를 정해 위, 아래로 붙은 바둑알 2개(이하 세로)와 좌, 우로 붙은 바둑알 2개(이하 가로)를 차례로 놓는다. 이때 도미니어링 게임이 펼쳐지는 게임판은 기존의 바둑판과는 다르다. 이 게임을 위한 맞춤형 게임판이 존재한다. 예를 들어, 그림 ❶과 같은 게임판에서는 순서에 관계없이 먼저 놓는 사람이 이긴다. 다음 차례에 해당하는 사람이 바둑알을 놓을 자리가 없기 때문이다.
그렇다면 그림 ❷와 같은 게임판에서는 누가 유리할까? 세로가 먼저 바둑알을 <;2>;<;3>;자리에 두면, 다음 차례인 가로가 놓을 자리가 없다. 반대로 가로가 먼저 바둑알을 둔다고 하면, 가로가 놓을 자리는 <;3>;<;4>;뿐이고 다음 차례인 세로가 <;1>;<;2>;에 바둑알을 두게 되므로 역시 가로가 지게 된다. 즉, 간단히 계산해 보면 이 게임판에서는 세로가 항상 이길 수 있다는 점을 알 수 있다.
이처럼 도미니어링 게임은 자신의 영역을 최대로 넓히면서 동시에 상대의 영역 확장을 사전에 막아야 하는 게임이다. 위의 예시처럼 게임판이 간단하면 승리 비법을 어렵지 않게 계산할 수 있다.
하지만, 게임판이 커지면 이야기는 달라진다. 위와 같은 게임판에서는 승리 비법을 쉽게 찾아내기 어렵다. 도미니어링 게임에서 이길 수 있는 가장 확실한 방법은 서로 놓을 수 있는 경우의 수를 전부 계산하는 것이다. 하지만 게임의 흐름이 시시각각 변하는 와중에 이를 계산하는 건 현실적으로 불가능에 가깝다. 따라서 매 순간 자신의 영역을 최대로 늘이기 위한 계산이 요구된다. 여기서 이를 수학적으로 설명하기 위해 ‘가치’와 ‘인센티브’의 개념이 등장한다.
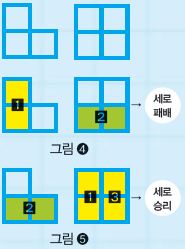
가치는 쉽게 말해 상대보다 자신이 승리할 수 있는 경우가 얼마나 많은지 보여 주는 수다. 그림 ❸과 같은 게임판에서는 세로가 가로에 비해 승리할 수 있는 경우의 수가 1가지 더 많다. 따라서 이 게임의 가치를 아래와 같은 식으로 표현하기도 한다.

그러나 높은 가치가 항상 승리로 직결되는 것은 아니다. 도미니어링 게임에서는 상대의 영역 확장을 사전에 막는 것이 중요하기 때문이다. 예를 들어 오른쪽과 같은 게임판이 있다고 하자. 이 게임에서 세로가 먼저 바둑알을 놓는다고 할 때, 둘 중 어느 게임판에 먼저 놓는 것이 유리할까? 세로가 왼쪽에 먼저 놓는다면 이 게임의 승자는 가로가 된다(그림 ❹). 하지만 반대의 경우에는 세로가 승리한다(그림 ❺). 즉, 세로에게는 오른쪽 게임판의 인센티브가 왼쪽보다 높다고 말할 수 있다.
도미니어링 게임은 바둑을 처음 접하는 사람이 바둑의 원리를 깨닫는 데도 도움이 된다. 가치와 인센티브를 따져가며 바둑알을 두는 과정이 바둑에서 자신의 ‘집’ 개수를 늘리는 데에도 적용될 수 있기 때문이다.
만지면서 푸는 퍼즐?
마지막으로 설명할 퍼즐은 지금까지 나온 퍼즐과는 큰 차이점이 있습니다. 바로 직접 손을 써가며 퍼즐을 움직여 풀어야 한다는 점! 이를 ‘기계적 퍼즐’이라고 하지요. 놀랍게도 기계적 퍼즐과 관련한 디자인 대회가 있고, 이 대회에서 대상을 수상한 한국인까지 있다고 합니다. 한 번 만나 볼까요?
퍼즐은 크게 눈으로 푸는 퍼즐과 손으로 푸는 퍼즐로 나뉠 수 있다. 눈으로 푸는 퍼즐이란, 앞서 소개했던 마방진과 복면산 등의 퍼즐을 총칭하는 것으로 논리퍼즐이라고 부르기도 한다. 손으로 푸는 퍼즐은 직접 만져가며 푸는 퍼즐을 말하는데, 마틴 가드너가 칼럼에 소개해 화제가 된 소마 큐브와 중국에서 시작된 칠교놀이 등이 대표적이다. 이처럼 손을 써가며 푸는 퍼즐을 ‘기계적 퍼즐’이라고 부른다.
기계적 퍼즐은 특성상 외형과 창의성이 퍼즐의 우수함을 판단하는 기준이 된다. 퍼즐이 보기에 신선하고 독창적일수록 좋은 평가를 받기 때문이다. 여기에 푸는 과정에서 재미를 찾을 수 있다면 더욱 훌륭한 퍼즐이 된다. 이 세가지 기준은 기계적 퍼즐을 대상으로 하는 국제퍼즐디자인대회의 수상 기준이기도 하다.
"퍼즐을 푸는 동안은 마냥 즐거워요."
현재 연세대학교에서 수학과 석사과정을 밟고 있는 안진후 학생은 2012년 국제퍼즐디자인대회(IPDC)에 처음 참가해 최고상인 심사위원 대상을 수상했다. 이 대회는 앞서 설명한 것처럼 기계적 퍼즐의 대가로 불리는 노부유키 요시가하라를 기리면서 퍼즐가들끼리 아이디어를 공유하는 대회다. 안진후 학생은 올해 대회도 참가해 선외 가작(본상 외의 상)을 수상했다. 그가 밝히는 퍼즐의 묘미는 뭘까.
“퍼즐을 푸는 동안은 마냥 즐거워요. 가장 희열을 느끼는 순간은 이른바 ‘아하! 모멘트’예요. 시행착오 끝에 퍼즐이 풀리는 순간 자연스럽게 입 밖으로 나오는 소리죠. 퍼즐에 깊게 몰두한 사람만이 느낄 수 있는 순간이라고 생각해요.”
어렸을 때부터 수많은 퍼즐을 섭렵하면서 수학에 흥미를 느낀 안진후 학생은 퍼즐을 하나하나 수집하다 보니 더 이상 구할 수 있는 퍼즐이 없어 직접 퍼즐을 만들게 되었다고 한다. 첫 퍼즐을 몇 개월 만에 제작한 그는 단순히 경험상 참가해 본 국제퍼즐디자인대회에서 최고상을 수상했다.
“당연히 믿기지 않았죠. 저는 단지 우리나라에도 기계적 퍼즐을 만드는 퍼즐가가 있다는 것을 보여 주고 싶어서 참가했거든요. 물론 저의 기계적 퍼즐 디자인 수준이 어느 정도인지 가늠하고 싶기는 했지만, 수상은 전혀 뜻밖이었어요.”
알파벳 G모양을 본뜬 그의 첫 퍼즐은 이후 ‘더블 G 퍼즐’이라는 이름으로 상품화되어 현재 시중에서 판매되고 있다.
“저는 기계적 퍼즐을 주로 다루는 오스카 반 디벤터와 베사 티모넨을 존경해요. 우리나라에도 이분들과 같이 퍼즐을 만드는 사람이 늘어나 퍼즐이 대중화 되었으면 하는 작은 바람을 가지고 있어요.”