d라이브러리

무한수의 덧셈

연초부터 각종 인터넷 포털 사이트에서 ‘1+2+3+4+…’ 꼴의 무한급수가 물의를 일으켰다. ‘물의’라는 표현이 이상하게 들리겠지만, 문제는 이 급수의 합이 다음과 같다는 주장 때문이었다.



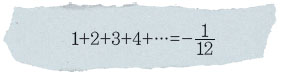
사실 이 등식은 상당히 오랜 역사를 가지고 있어서 18세기 수학의 대가 오일러가 거론하기도 했었다. 그런데 최근 ‘수 애호가(Numberphile)’라는 수학 대중화 인기 웹사이트에서 이 등식의 중요성에 대한 동영상이 화제였다. 동영상의 초점은 산술적 방법론이 비교적 자연스러운 편법을 통해 상상하지 못할 결과를 초래한다는 일종의 신비감을 전해 주는 것이었다.

해석에 따라서 아주 재미있게 설명했다 할 수 있지만, 그런 관점 때문에 생기는 혼란을 걱정하는 수학자도 많았다. 편법의 재미와 엄밀한 논리는 확실하게 구별해야 한다는 입장도 당연히 타당하다.

물론 위와 같은 등식은 성립하지 않는다. 그러나 이번 사건은 지금처럼 과학 문명이 발전한 사회에서도 ‘무한’이라는 개념이 얼마나 많은 어려움과 두려움을 내포하고 있는지를 보여 준다.

가령 중학교 수준의 수학에서도 0.9999…=1이라는 혼란스러운 등식을 만날 수 있다. 혼란스러운 이유는 등식의 왼쪽, 즉 소수점 다음에 9가 계속 된다는 게 무슨 뜻인지 그 의미를 설명하지 않기 때문이다. 수를 표기할 때 9999=9×1000+9×100+9×10+9×1인 것처럼 사실은 0.9999…이란 수는 9×0.1+9×0.01+9×0.001+9×
0.0001+…, 즉 무한히 많은 작은 수를 더해서 만든 것이다. 그렇게 해석하면 답이 1이라는 것은1/2+1/4+1/8+ 1/16+…=1만큼 자연스러운 사실이다.

아무튼 현대 과학에서 무한이라는 개념 없이 작업하는 은 불가능한 일이다. 물리학자들은 우주가 무한하다는 반적인 믿음을 갖고 있고, 더 기초적인 수준에서 직선상의 점이 몇 개냐고 물으면 무한하다는 것이 상식적인 답이다. 이뿐만이 아니라 거의 모든 자연과학의 기초인